Time Value of Money - A Fundamental Concept | SBI PO Prelims & Mains Preparation - Bank Exams PDF Download
Concept
- Time value of money is the fundamental concept of Investment and Finance. It is the basic concept that says that money has different values over the different point of time e.g. a money today may be worth more than it is a few years ahead.
- Time value is associated with money due to various factors like – inflation, the uncertainty of the market, interest rates etc.
- It is necessary to analyse the value of money before investing it.
- Returns are calculated based on interest rates offered in the market.

- There are two types of Interest Rates viz. Simple Interest and Compound Interest.
- Simple Interest = Principal x Rate x Time
- Future value on investment = Principal + Simple Interest
- Compound Interest: In this method of calculation, interest is calculated on the accumulated interest.
- Future Value of Investment = P (1+R)T
- Compounding is also done at various intervals like monthly, annually, semi-annually, quarterly etc., the above formula changes to
- Future Value of Investment = P (1 + R/n)Txn
- where n is the number of time compounding is done during a year.
Example: 1
Ram invested ₹1000 in a Bank for 2 years that offers 10% Interest P.A. at simple interest, how much will Ram get in return after 2 years?
Sol: Return Amount = P + SI = 1000 + (1000 x 0.1 x 2)
= 1000 + 200 = ₹1200,
hence Ram will get ₹1200 after 2 years from the bank.
Example: 2
If Ram had invested ₹1000 in a Bank for 2 years that offers 10% Interest P.A. at compound interest, how much will Ram get in return after 2 years?
Sol: Return Amount = P (1+R)T= 1000(1 + 0.1)2 = ₹1210.00
Note: The difference between CI and SI amount in above example is due to the Compounding Power i.e. calculating interest on interest.

Annuities
- Annuity is a fixed sum of money that is paid at regular intervals e.g. Insurance premium, pension payment etc.
Example:
Ashok receives ₹5000.00 per month as a pension, this is an annuity.
Ramesh pays ₹20000.00 per year as Life Insurance premium, this is an annuity.
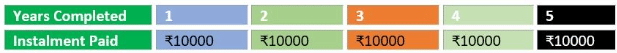
If the amount paid is variable at intervals, then it is called as uneven cash flow instead of Annuity.
Important points
- The present value of a perpetuity is A/R, where A is the periodic payment to be received forever and the expected rate of interest is r%. This is very important in calculations like share price, for example:
Example: M/S ABC pays an annual dividend of ₹10 indefinitely then what should be the per-share price of M/S ABC to attract the investors assuming no capital growth in share price and rate of return expected is 5%
Solution: PV of all the dividends received is = A/r =10/.1 = ₹100, if M/S ABC will keep share price below ₹100 then the investor will be attracted as it will be profitable considering the fact that the net present value of dividends will be more than the investment, however, if the company quotes share price more than ₹100 then the investors will not get attracted to the scheme.
Rule of 72: This is a simple rule to find out that if the rate of interest is x%, then in how many years the invested amount will double itself. The rule says that the amount invested will get doubled in 72/x years.
For example: if the rate of interest is 12% PA, then the invested amount will double itself in 72/12 i.e. 6 years
Inflation
- Inflation implies reduced purchasing power of money which is due to rising prices of commodities.
- CI and SI impact the final returns adversely, at small levels i.e. few years the difference may seem negligible, but at large scales the difference s tremendous as shown below, the blue line is the amount in case of compound interest and the other line is for Simple Interest.
|
628 videos|824 docs|280 tests
|
|
628 videos|824 docs|280 tests
|

|
Explore Courses for Bank Exams exam
|

|
















