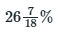Overview: Time & Work | CSAT Preparation - UPSC PDF Download
Introduction
Time and Work is an important topic in competitive exams. The questions related to time and work hold significant weight due to their various applications.

Time and work deals with the time taken by an individual or a group of individuals to complete a piece of work and the efficiency of the work done by each of them.
The problems on Time and Work fall into two categories:
- Finding the time required to complete the assigned job.
- Finding the work done in a given time period.
What is Time & Work?
Work is defined as something which has an effect or outcome; often the one desired or expected. The basic concept of Time and Work is similar to that across all Arithmetic topics, i.e., the concept of Proportionality.
Efficiency is inversely proportional to the time taken when the amount of work done is constant.
i.e., Efficiency ∝ 1/Time taken.
Concept of Time & Work
If a man can complete a work in 'n' days, then workdone in 1 day = 1/n,
And this one day's work in terms of percentage is called Capacity.
- If a man can complete 1/n work in one day, he can complete the whole work in n days.
- Here, we assume that total work is one (unit); the number of days required to complete the given work would be equivalent to the reciprocal of the day's work.
If A can complete his work in a days, then A's one day's work = 1/a
If B can complete his work in b days, then B's one day's work = 1/b
If A and B work together in one day, then their combined work is 1/a + 1/b or (a+b)/ab
These types of problems can be solved through three methods:
- Unitary method
- Percentage capacity
- LCM approach (Best Approach)
The unitary method is obsolete due to its difficult calculations.
Note:
- More men less days and conversely more days less men.
- More men more work and conversely more work more men.
- More days more work and conversely more work more days.
Approaches
1. Percentage Approach
Instead of taking the value of the total work as 1 unit of work, we can also look at the total work as 100 per cent of the work. In such a case the following rule applies:
- If A does a work in a days, then in one day A does 100/a % of the work
- If B does a work in b days, then in one day B does 100/b % of the work
- Then, in one day, if A and B work together, their combined work is 100/a + 100/b
Example: If A can do a work in 10 days and B can do the same work in 12 days, then the work will be completed in how many days?
Sol: One day work for A = 100/10 % = 10%, One day work for B = 100/12% = 8.33%
Total work in one day = 10% + 8.33% = 18.33%
Total days needed = 100/18.33 = 5.45 days
2. LCM Method (The Best Approach)
LCM method is best explained using an example. Let's use the same example used above.Example: If A can do a work in 10 days and B can do the same work in 12 days, then the work will be completed in how many days?
Sol:Take LCM of 10,12 i.e. 60, Assume this to be the Total work.
A can do the work in 10 days; hence, He would do 6 units of work per day (60/10)
B can do the work in 12 days; hence, He would do 5 units of work per day (60/12)
Combined Units of work per day = 6 + 5 = 11
Total days needed = Total work/Combined work per day = 60/11 = 5.45
Concept of Negative Work
- Suppose X and Y are working together to build a wall but Z is working to break the wall. In this case the wall is being build by X and Y but being broken by Z.
- Here if we consider the work to build a wall is positive,
then, we can say that Z is doing negative work. - Mathematically, If 1 person makes something in A days and another breaks it in B days. then,
- Work done per day = 1/A - 1/B = (B-A)/ AB
and No. of Days = AB/(B-A)
Example : Amit can build a wall in 6 hours but Rohit can destroy the same in 10 hours. If both work simultaneously, how many hours are required to actually build the wall?
Sol: Amit builds the wall in 6 hours (Positive Work)
Rohit destroys the wall in 10 hours (Negative Work)
Work Done by Amit in 1 hour = 1/6
Work Done by Rohit in 1 hour = 1/10
Work done per hour = 1/6 - 1/10
= 2/30
= 1/15
No. of hours required to complete the wall = 15 hours
Application of Product Constancy Table
The basic equation that applies to to Time and Work is Work done = Work Rate x Time
- This equation shows that when the work done is the same, the work rate changes inversely with the time taken.
As a result, the Product Constancy Table will be directly used with the questions of time and work.
Time is usually in days or hours. The unit of time that is used in a question is usually decided by the denominator of the unit of workrate.
So, there are two ways in which we can define the work rate - Individual Working Efficiencies
In the questions where Individual working efficiencies or Individual working time is given, the work rate is defined as Work done/time
In this case, total work is considered to be 1(if we solve through fractions) and 100% (if we solve through percentage)
Example: If A can do a piece of work in 10 days and B can do the same in 12 Days. In how many days A and B can together do the work?
Sol: We will solve this question through percentage method
One day's work = 10% + 8.33% = 18.33%
therefore A and B together do 18.33% of the work in a day
thus we can say that
18.33% of the work x No of days required = 100% of the work
No. of days required = 100/18.33 = 5.45
So we concluded that when individual work done is given, we define work rate as work done/ time and take total work = 100% or 1
- Tasks are completed by a certain category of workers
In this type where a certain category of workers are working on a task or a project, the work rate will be defined as number of workers of a particular category working on a project. In such cases the work to be done is taken as number of hours required to finish the work.
Work Equivalence Method
- The Work Equivalence Method is nothing but an important application of Time and Work Problems.
- We already know the formula i.e Work Rate x Time = Work Done.
- Now, Work Equivalence Method says that if we double the Work Done, then the (Work rate x time) should also get doubled.
- Similarly, if the Work done is to be increased by 20% then the product (Work Rate x Time) should also be increased by 20 % and followed on like that.
Example: A Carpenter estimates that he will complete his project in 100 days by employing 50 men. However at the end of 50th day, when as per his estimation half the work should have been completed, he finds that only 40% of the work is done.
a. How many more days will be required to complete the work?
b. How many more men should he employ in order to complete his work on time?
Sol: a) The Carpenter has completed 40% of his work in 50 days.
If number of men remains the same, the rate at which the work is going on remains the same.
Hence the remaining work i.e 60% of the work will be completed in 75 days(solved using Unitary method)
therefore, 75 more days are required to completed the whole project.
b) Now, if he wants to completed the work on time, he have to employ more men working on the project.
50 men working for 50 days = 2500 man days
=> 2500 man days are required to complete 40% of the task
Work left = 60%
Left work can be completed in = 2500x 60/40 = 2500 x 1.5
= 3750 man days
This has to be completed in 50 days
therefore, number of men = 3750 / 50 = 75 men.Since 50 men are already working , the additional men needed are :
75-50=25 men
Pipes and Cistern
- We employ the same basic concepts of ‘Time and Work’ to solve questions based on pipes and cisterns. However, in some instances in addition to inlet pipes, the question also mentions outlet pipes.
- A pipe connected to the cistern is called an Inlet pipe or an Outlet pipe, accordingly as it fills it or empties it respectively.
- To make the principle of work and time to work here, we assume that the inlet pipes are doing positive work and the outlet pipes are doing negative work and the concept behind solving these questions remains the same.
Example: Two pipes A and B can fill a tank in 20 and 30 minutes respectively, and a third pipe C can empty it in 40 minutes. How much time will it take to fill the tank if all the three are opened at the same time?
Sol: LCM of 20, 30, and 40 = 120.
Let us assume that the capacity of the tank is 120 liters.
Therefore,
Rate of pipe A = 120/20 = 6 litres/min
Similarly, Rate of pipe B = 120/30 = 4 liters/min
And rate of pipe C = 120/40 = 3 liters/min
All three pipes are opened simultaneously, then in a minute,
the amount of water in the tank in a min will be =6+4-3 =7 liters.
As pipe C is an outlet pipe, we are taking its work to be negative.
Hence, the time taken to fill the cistern = 120/7 min.
So, from the above explanation its obvious that the problems from pipes and cisterns are an extension of work and time.
Important concepts on Pipes and Cistern
1. The time required by the leak pipe alone to empty the tank
- If an inlet pipe takes 'x' minutes to fill a cistern,
- But due to a leak, it takes an additional 'y' minutes to fill the cistern,
- Then, the time it takes for the leak to completely empty the full cistern, when the inlet pipe is not working is
 minutes.
minutes.
Example If a tank generally takes 20 min to be filled by a pipe, but due to leak, it takes 10 extra min to be filled, then the amount of time in which the leak can empty the full tank is?
Sol: On comparing, we have x=20 and y=10. Therefore, the leak will take 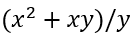 minutes.
minutes.
putting the values of x and y, we get (202+20x10)/10 = 60 minutes
2. Finding the capacity of the tank
A cistern has a leak which can empty it in 'a' hours. A pipe which admits 'b' liters of water per hour into the cistern is turned on, and now the cistern is emptied in 'c' hours. Then the capacity of the cistern is liters is (a x b x c)/(c-a)
Example : A tank has a leak which can empty it in 4 hours. A pipe which admits 20 liters of water per hour into the tank is turned on, and now the tank is emptied in 6 hours. What is the capacity of the tank?
Sol: By comparing with the shortcut formula, a=4, b=20, and c=6. Therefore, the capacity of the tank =(a x b x c)/(c-a)
putting the values of a, b and c , we get
(4x20x6)/(6-4) = 240 litre.
3. Pipes opened for different durations:
If two pipes A and B are opened for different time periods, then to solve the question we use
A’s amount of work +B’s amount of work=1.
(A's open time/ Alone fill time of A) + (B's open time/ Alone fill time of B) = 1
Example : Two pipes A and B can fill a cistern in 12 and 16 min respectively. Both pipes are opened together but 4 min before the cistern is full, one pipe A is closed. Find the time required to fill the cistern?
Sol: Let it takes x min by the pipes A and B to fill the cistern.
Therefore, the duration for which pipe was operating = (x-4) min. And pipe B was operating for x min.
Now, substituting in the formula given above, we get:
(x-4)/12 + x/16 = 1
(4x-16+3x)/48 = 1
x = 64/7 minute
therefore , it takes 64/7 minutes to fill a cistern
4. Rate of flow of the pipe is proportional to the diameter.
Example: There are three inlet pipes whose diameters are 1 cm, 2 cm, and 4 cm respectively. The rate of flow of water is directly proportional to the square of the diameter. The pipe with the largest diameter takes 16 min to fill a cistern. How much time it will take for all three pipes, working together, to fill the cistern.
Sol: Let the three pipes be A, B, and C respectively.
Therefore,
For pipe A, the rate of flow per min = k(1)2 = k
Similarly, the rate of flow per min of pipe B = k(2)2 =4k
And, the rate of flow per min of pipe C = k(4)2 =16k, where k is a proportionality constant.
It is given that the pipe C can alone fill the cistern in 16 min.
Hence, the capacity of cistern = the rate of flow of pipe C×time taken by the pipe C=16k×16=256k liters.
Now, when all three pipes operate together, the combined rate of flow per min = k+4k+16k=21k.
Therefore, the time required to fill the cistern = 256k/21k=256/21 minutes
Important Formulas
Type - 1: Basic Formula
- If M1 men can do W1 work in D1 days and M2 men can do W2 work in D2 days, then:

- If we include working hours T1 and T2 for two groups, then:
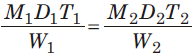
- If M1 men of E1 efficiency can do W1 work in D1 days with T1 working hours/day and M2 men of E2 efficiency can do W2 work in D2 days with T2 working hours/day, then:
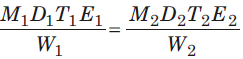
Let's look at some examples.

Example 1. A contractor adopts a work to complete it in 100 days. He employed 100 workers. But after 50 days it was found that only 1/3rd of the work has completed, How many more workers he should employ to complete the work in time.
(a) 100
(b) 125
(c) 150
(d) 175
Ans: Option (a) is correct.
Sol: 100 men in 50 days can do 1/3rd of the work.
No. of men required to complete 2/3rd of the work in 50 days will be:
Hence, x = 100
Example 2: If 25 men can do a piece of work in 36 days working 10 hours a day, then how many men are required to complete the work working 6 hours a day in 20 days?
(a) 65
(b) 75
(c) 84
(d) 92
Ans: Option (b) is correct.
Sol: M1 x D1 x H1 = M2 x D2 x H2
⇒ 25 x 36 x 10 = M2 x 20 x 6
⇒ M2 = 75 persons
Alternatively:
By percentage change graphic, when time is decreased by 2/3 ( i.e., 66.66%), the number of men is increased by 2 times (i.e., 200%)
Example 3: A contractor employed a certain number of workers to finish construction of a road in a certain scheduled time. Sometime later, when a part of work had been completed, he realised that the work would get delayed by three-fourth of the scheduled time, so he at once doubled the number of workers and thus he managed to finish the road on the scheduled time. How much work had been completed, before increasing the number of workers?
(a) 10%
(b) 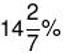
(c) 12 %
(d) 15 %
Ans: Option (b) is correct.
Sol: Let he initially employed x workers which works for D days and he estimated 100 days for the whole work and then he doubled the workers for (100 - D) days.
D * x + (100 - D) * 2x = 175x
D = 25 days
Note: 175 = 100 + (3/4) x 100, Since required number of days are 75% i.e (3/4) more than the estimated number of days.
Now, the work done in 25 days = 25x
Total work =175x
∴ Work done before increasing the number of workers =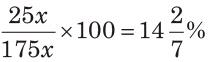
Type - 2: When 2 persons are working
If A can do a piece of work in x days and B can do it in y days then A and B working together will do the same work in 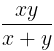 days.
days.
Let's look at some examples related to it.
Example 4: A and B can do a piece of work in 12 days, B and C in 15 days C and A in 20 days. How long would each take separately to do the same work?
(a) A = 20 days, B = 30 days, C = 50 days
(b) A = 30 days, B = 20 days, C = 60 days
(c) A = 20 days, B = 20 days, C = 50 days
(d) A = 30 days, B = 40 days, C = 30 days
Ans: Option (b) is correct.
Sol: A + B can do in 12 days, B + C can do in 15 days, and A+ C can do in 20 days.
2(A+ B + C) =
∴ A+ B + C can do the work in 5 x 2 =10 days. (less men more days)
Now,
⇒ A can do the work in =[As, A =(A+ B + C) - (B + C)]
⇒ B can do the work in =[As, B = (A+ B + C) - (A+ C)]
⇒ C can do the work in =
Type - 3: When 3 persons are working
If A, B, and C do a work in x, y, and z days respectively then all three working together can finish the work in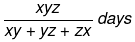
Let's see an example.
Example 5: A can complete a work in 10 days B in 20 days and C in 25 days. If they work together in how many days they can complete the work.
(a) 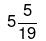
(b) 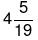
(c) 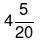
(d) 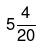
Ans: Option (a) is correct.
Sol: To find out how long it takes for A, B, and C to complete a work when they work together, you can use the concept of their individual work rates.
A can complete the work in 10 days, so his work rate is 1/10 of the work per day. B can complete the work in 20 days, so his work rate is 1/20 of the work per day. C can complete the work in 25 days, so his work rate is 1/25 of the work per day.
When they work together, their work rates add up:
Work rate of A + Work rate of B + Work rate of C = 1/10 + 1/20 + 1/25
To add these fractions, you can find a common denominator, which is 200: (20/200) + (10/200) + (8/200) = (20 + 10 + 8) / 200 = 38/200
Now, their combined work rate is 38/200 of the work per day.
To find out how many days it will take for them to complete the work together, take the reciprocal of their combined work rate: 1 / (38/200) = 200 / 38 = 100 / 19
So, when A, B, and C work together, they can complete the work in approximately 5.26 days or
Type - 4: How many days to the work alone?
If A and B together can do a work in x days and A alone can do it in y days then B alone can do it in xy/(y-x) days.
Let's solve an example on this.
Example 6: The rate at which tap M fills a tank is 60% more than that of tap N. If both the taps are opened simultaneously, they take 50 hours to fill the tank. The time taken by N alone to fill the tank is (in hours):
(a) 90 hours
(b) 110 hours
(c) 130 hours
(d) 150 hours
Ans: Option 'c' is correct.
Sol: Since the rate at which tap M fills the tank is 60% more than that of tap N, the rate at which tap M fills the tank is 1.6 times the rate of tap N. So, the rate at which tap M fills the tank is 1.6x units per hour.
When both taps are opened simultaneously, they can fill the tank in 50 hours.
So, the combined rate of both taps is 1 tank per 50 hours, or 1/50 tanks per hour.
The combined rate is the sum of the individual rates: x (rate of N) + 1.6x (rate of M) = 1/50Now, solve for x:
2.6x = 1/50x = (1/50) / 2.6
x = 1/50 * 1/2.6
x = 1/130
So, tap N fills 1/130 of the tank per hour.
Now, to find the time taken by N alone to fill the tank, take the reciprocal of its rate:
Time taken by N alone = 1 / (1/130)
Time taken by N alone = 130 hours
Therefore, it takes tap N 130 hours to fill the tank on its own.
Type - 5: Variation between Time and Work
- When the value of one quantity increases with respect to decrease in other or vice-versa, then they are said to be inversely proportional. It means that the two quantities behave opposite in nature.
- Efficiency is inversely proportional to the number of days (D) taken to complete the work. Means,
E ∝ 1/D or E = K/DWhere K is constant ∴ ED = constant
Similarly, E1D1 = E2D2 - These product methods are limited to the constant work, if the amount of work gets changed, then it does not work, then we have to take help from the Unitary method.
- In the unitary method, the value of a unit quantity is calculated first to calculate the value of other units. It has two types of variations:
(i) Direct Variation: In direct variation, increase or decrease in one quantity will cause an increase or decrease in another quantity. For instance, an increase in the number of goods will cost more price.
(ii) Inverse Variation: It is the inverse of direct variation. If we increase a quantity, then the value of another quantity gets decrease. - When more than one man works on a particular work, the rate of work is calculated as the strength of workers working at a particular time. So, the amount of work is defined in terms of men days or man-hours or man-days-hours.
Example 7: A takes 16 days to finish a job alone, while B takes 8 days to finish the same job. What is the ratio of their efficiency and who is less efficient?
(a) 1 : 2
(b) 1 : 3
(c) 2 : 3
(d) 3 : 4
Ans: Option (a) is correct.
Sol: Since A takes more time than B to finish the same job hence A is less efficient.
Efficiency of A = 100/16 = 6.25 %
Efficiency of B = 100/8 = 12.5 %
Ratio of efficiency of A and B,
Hence, B is twice efficient as A.
Note:
∴ Efficiency * Time taken = Constant workWhole work is always considered as 1, in terms of fraction and 100%, in terms of percentage.In general, the number of days or hours = (100 / Efficiency)
If you require a teacher's help to understand practise questions regarding topic "Time & Work", watch the video given below:
Let's practice few questions on Time & Work.
Practice Questions
Q 1: A can complete a work in 10 days, B in 12 days and C in 15 days. All of them began the work together, but A had to leave the work after 2 days of the start and B 3 days before the completion of the work. How long did the work last?
(a) 5
(b) 6
(c) 7
(d) 8
Ans: Option (c) is correct.
Sol: See the diagram and then interpret the language of the question
Since initially for 2 days all of them A,B and C work together so they complete he 50% work and for the last 3 days only C works which is equal to 20% work.
Thus, the remaining work = 30%[100 - (50 + 20)]
This 30% work was done by B and C in 2 days = (30/15)
Note:
Efficiency of A =10%
Efficiency of B = 8.33%
Efficiency of C = 6.66%
So, the total number of required days = 2 + 2 + 3 = 7 days.
Q 2: Arun and Satyam can complete a work individually in 12 days and 15 days respectively. Arun works only on Monday, Wednesday and Friday while Satyam does the work on Tuesday, Thursday and Saturday. Sunday is always off. But Arun and Satyam both work with half of their efficiencies on Friday and Saturday respectively. If Arun started the work on 1st January which falls on Monday followed by Satyam on the next day and so on (i.e., they work collectively on alternate days), then on which day work will be completed?
(a) Tuesday
(b) Thursday
(c) Friday
(d) Saturday
Ans: Option (b) is correct.
Sol: This pattern continued for total 2 weeks only till 75% work got completed.
Thus in 2 weeks they will complete 75% work.
Now 15% of the remaining (25% of the work) will be done in the third week on Monday and Tuesday. Again 10% work remained undone. Out of this 8.33 work will be done by Arun on Wednesday and remaining 1.66% work will be completed on Thursday by Satyam.
Hence the work will be completed on Thursday.
Q 3: In the ancient city of Portheus, the emperor has installed an overhead tank that is filled by two pumps X and Y. X can fill the tank in 12 hours while Y can fill the tank in 15 hours. There is a pipe Z which can empty the tank in 10 hours. Both the pumps are opened simultaneously. The supervisor of the tank, before going out on a work, asks his assistant to open Z when the tank is exactly 40% filled so that the tank is exactly filled up by the time he is back. If he starts X and Y at exactly 11:00 AM and he comes back at A : B. Then find the value of A + B.
(a) 40
(b) 41
(c) 42
(d) 43
Ans: Option (b) is correct.
Sol: Let the total capacity of the tank be 180 litres:
Efficiency of X = 15 l/hr.
Efficiency of Y = 12 l/hr.
Efficiency of Z = 18 l/hr.
Time taken to fill the tank to 40% of it's capacity (i.e., 72 litres) = 72/27 = 2 hours 40 minutes.
After 2 hours 40 minutes, Z starts working.
The rate at which the tank would be filled after this would be : 15 + 12 – 18 = 9 litres per hours.
The total quantity to be filled in order to fill up the tank = 180 – 72 = 108.
This will take 108/9 = 12 hours to complete. Hence, the supervisor comes back after: 12 hours + 2 hours 40 minutes = 14 hours 40 minutes.
Hence, he is supposed to come back at: 1:40 AM (the next day).
The value of A + B = 41.
Q 4: Three pipes, A, B and C, can fill a cistern in 12, 18 and 24 minutes, respectively, If all the pipes are opened together for 7 minutes, what will be the volume of the water that overflows as the percentage of the total volume of the cistern?
(a) 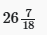
(b)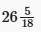
(c)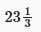
(d) 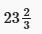
Ans: Option (a) is correct.
Sol:
Total work = 72
Work done by pipe A, B and C in 7 min = (6 + 4 + 3) × 7 = 91
Volume of the water that overflows = 91 – 72 = 19
Required percentage = (19/72) × 100 =
Q 5: A contract is to be completed in 72 days and 104 men are set to work, each working 8 hours a days. After 30 days, only 1/5th of the work is finished. How many additional men need to be employed so that the work may be completed on time. (If each man is now working 9 hours per day)?
(a) 153 men
(b) 155 men
(c) 158 men
(d) 161 men
Ans: Option (d) is correct.
Sol: Using the work equivalence method, we know that 1/5th of the work =104 x 30 x 8 man-hours.
Thus, the remaining work = 4 x 104 x 30 x 8.
Since this work has to be done in the remaining 42 days by working at 9 hours per day,
The number of men required would be given by: ( 4 x 104 x 30 x 8) ÷ (42 x 9) = 264.12 = 265 men.
This means that we would need to hire 161 additional men.
Q 6: Two pipes can fill a cistern in 14 and 16 hours respectively. The pipes are opened simultaneously and it is found that due to leakage in the bottom of the cistern, it takes 32 minutes extra for the cistern to be filled up. When the cistern is full, in what time will the leak empty it?
Sol: The 32 minutes extra represents the extra time taken by the pipes due to the leak.
Normal time for the pipes → n * (1/14 +1/16) = 1→ n =112 /15 = 7 hrs 28 minutes.
Thus, with 32 minutes extra, the pipes would take 8 hours to fill the tank.
Thus, 8(1/14 +1/16) -8 * (1/L) =1 → 8 /L
= 8(15 /112) -1
1/L=15 /112 -1/8
=1/112.
Thus, L =112 hours.
|
208 videos|272 docs|138 tests
|
FAQs on Overview: Time & Work - CSAT Preparation - UPSC
| 1. What is the basic concept of Time & Work in mathematics? |  |
| 2. How do you apply the Product Constancy Table in Time & Work problems? |  |
| 3. What is the concept of Negative Work in Time & Work problems? |  |
| 4. How does the Pipes and Cistern method work in Time & Work questions? |  |
| 5. What are some important formulas used in Time & Work calculations? |  |


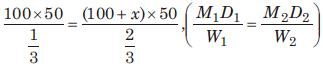
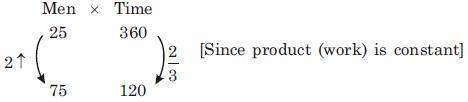

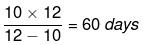

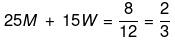
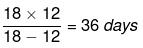
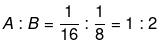
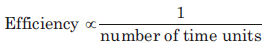
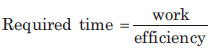
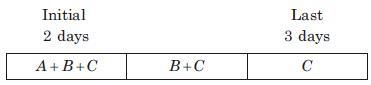

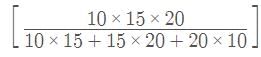 days
days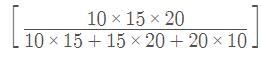 =
= 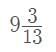 days
days