Tips and Tricks: Division | Improve Your Calculations: Vedic Maths (English) - Class 6 PDF Download
| Table of contents |

|
| Defining the Division terms |

|
| Special Methods of Division |

|
| Straight Division |

|
| Split Method |

|
Defining the Division terms
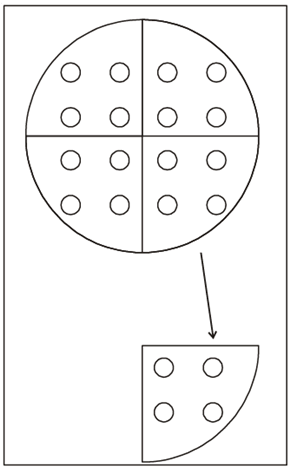 There are 16 balls to be distributed among 4 people How much each one will get is a problems of division.
There are 16 balls to be distributed among 4 people How much each one will get is a problems of division.
Let us use this example to understand the terms used in division:
- Divisor: Represent number of people we want to distribute them or the number that we want to divide by. Here the divisor is 4.
- Dividend: Represents number of balls to be divided 16 in this case.
- Quotient: Represents the number of balls in each part, 4 is this case.
- Remainder: What remains after dividing in equal parts, 0 in this case?
The remainder theorem follows from the division example above and is expressed mathematically as follows.
Divided = Divisor × Quotient + Remainder The remainder theorem can be used to check the Division sums in Vedic Mathematics as described in the following sections.
Different methods are used for dividing numbers based on whether the divisor is single digit numbers below a base, above a base or no special case.
Special Methods of Division
Number splitting
Simple Division of Divisor with single digits can be done using this method.
Example: The number 682 can be split into
6/82 and we get 3/41 because
6 and 82 are both easy to halve
Therefore 682/2 = 341
Example: 3648/2 becomes
36/48/2 = 18/24 = 1824
Example: 1599/3 we notice that 15 and 99 can be separately by 3 so
15/99/3 = 5/33 = 533
Example: 618/6 can also be mentally done
6/18/6 = 103 note the 0 here
Because the 18 takes up two places
Example: 1435/7
14/35/7 = 2/05 = 205
Example: 27483/3 becomes
27/48/3/3 = 9/16/1 = 9161
Division by 9
As we have seen before that the number 9 is special and there is very easy way to divide by 9.
Example 1: Find 25 ÷ 9
25/9 gives 2 remainder 7
The first figure of 25 is the answer?
And adding the figures of 25 gives the remainders 2 + 5 = 7 so 25 ÷ 9 = 2 remainder 7. It is easy to see why this works because every 10 contains 9 with 1 left over, so 2 tens contains 2 times with 2 left over. The answer is the same as the remainders 2. And that is why we add 2 to 5 to get remainder. It can happen that there is another nine in the remainder like in the next example.
Example 2: Find 66 ÷ 9
66/9 gives 6 + 6 = 12 or 7 or 3
We get 6 as quotient and remainder 12 and there is another nine in the remainder of 12, so we add the one extra nine to the 6 which becomes 7 and remainder is reduced to 3 (take 9 from 12) We can also get the final remainder 3, by adding the digits in 12. The unique property of number nine that it is one unit below ten leads to many of the very easy Vedic Methods.
This method can easily be extended to longer numbers.
Example 3: 3401 ÷ 9 = 377 remainder 8
Step 1: The 3 at the beginning of 3401 is brought straight into the answer.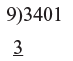 Step 2: This 3 is add to 4 in 3401 and 7 is put down
Step 2: This 3 is add to 4 in 3401 and 7 is put down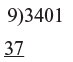 Step 3: This 7 is then added to the 0 in 3401 and 7 is put down.
Step 3: This 7 is then added to the 0 in 3401 and 7 is put down.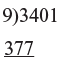 Step 4: This 7 is then added to give the remainder
Step 4: This 7 is then added to give the remainder
9) 340/1
377/8
Longer numbers in the divisor
The method can be easily extended to longer numbers. Suppose we want to divide the number 21 3423 by 99. This is very similar to division by 9 but because 99 has two 9’s we can get the answer in two digits at a time. Think of the number split into pairs.
21/34/23 where the last pair is part of the remainder.
Step 1: Then put down 21 as the first part of the answer Step 2: Then add 21 to the 34 and put down 55 as next part
Step 2: Then add 21 to the 34 and put down 55 as next part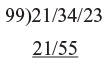 Step 3: Finally add the 55 to the last pair and put down 78 as the remainder
Step 3: Finally add the 55 to the last pair and put down 78 as the remainder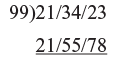 So the answer is 2155 remainder 78
So the answer is 2155 remainder 78
Example 1: 12/314 ÷ 98 = 1237
Step 1: This is the same as before but because 98 is 2 below 100 we double the last part of the answer before adding it to the next part of the sum. So we begin as before by bringing 12 down into the answer.
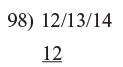 Step 2: Then we double 12 add 24 to 13 to get 37
Step 2: Then we double 12 add 24 to 13 to get 37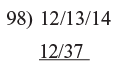 Step 3: Finally double 37 added 37 × 2 = 74 to 14
Step 3: Finally double 37 added 37 × 2 = 74 to 14
98)12/13/14
12/37/88 =1237 remainder 88.
It is similarly easy to divide by numbers near other base numbers 100, 1000 etc.
Example 2: Suppose we want to divide 236 by 88 (which is close to 100). We need to know how many times 88 can be taken from 235 and what the remainder is
Step 1: We separate the two figures on the right because 88 is close to 100 (Which has 2 zeros)
88) 2/36
Step 2: Then since 88 is 12 below 100 we put 12 below 88, as shown
88) 2/36
Step 3: We bring down the initial 2 into the answer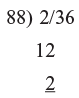 Step 4: This 2 is multiplies Haggled 12 and the 22 is placed under the 36 as Shown
Step 4: This 2 is multiplies Haggled 12 and the 22 is placed under the 36 as Shown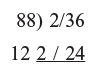 Step 5: We then simply add up the last two columns.
Step 5: We then simply add up the last two columns.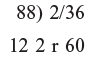 In a similar way we can divide by numbers like 97 and 999.
In a similar way we can divide by numbers like 97 and 999.
Sutra: Transpose and Apply
A very similar method, allows us to divide numbers, which are close to but above a base number.
Example: 1479 ÷ 123 = 12 remainder 13
Step 1: 123 is 23 more than base 100
Step 2: Divide 1479 in two columns therefore of 2digit each
Step 3: Write 14 down
Step 4: Multiply 1 by 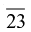 and write it below next two digits. Add in the Second column and put down 2.
and write it below next two digits. Add in the Second column and put down 2.
Step 5: Add multiply this 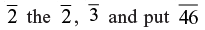 then add up last two Columns
then add up last two Columns
Straight Division
The general division method, also called Straight division, allows us to divide numbers of any size by numbers of any sine, in one line, Sri BharatiKrsnaTirthaji called this “the cowing gem of Vedic Mathematics”
Sutra: - ‘vertically and crosswise’ and ‘on the flag’
Example 1: Divide 234 by 54
The division, 54 is written with 4 raised up, on the flag, and a vertical line is drawn one figure from the right hand end to separate the answer, 4, from the remainder 28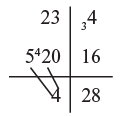 Step 1: 5 into 20 goes 4 remained 3 as shown
Step 1: 5 into 20 goes 4 remained 3 as shown
Step 2: Answer 4 multiplied by the flagged 4 gives 16 and this 16 taken from 34 leaves the remainder 28 as shown
Example 2: Divide: 507 by 72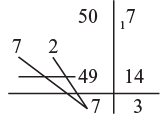 Step 1: 7 into 50 goes 7 remainder 1 as shown
Step 1: 7 into 50 goes 7 remainder 1 as shown
Step 2: 7 times the flagged 2 gives 14 which we take from 17 to have remainder of 3
Split Method
Split method can be done for division also. For example:
6234 ÷ 2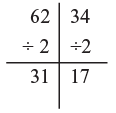 The 'split' may require more 'parts'.
The 'split' may require more 'parts'.
30155 ÷ 5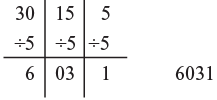 244506 ÷ 3
244506 ÷ 3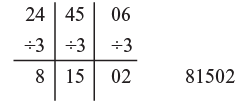
|
38 videos|31 docs|9 tests
|




















