Tips and Tricks: Fractions & Decimals | Quantitative Aptitude for SSC CGL PDF Download
Tips For Numbers Decimals Fractions
1. (a – b)2 = (a2 + b2 – 2ab)
2. (a + b)2 = (a2 + b2 + 2ab)
3. (a + b)(a – b) = (a2 – b2)
4. (a3 + b3) = (a + b)(a2 – ab + b2)
5. (a3 – b3) = (a – b)(a2 – ab + b2)
6. (a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca)
7. (a3 + b3 + c3 – 3abc) = (a + b + c)(a2 + b2 + c2 – ab – bc – ac)
Tricks and shortcuts for Decimal and fraction
Decimal Fractions
Fractions in which denominators are powers of 10 are known as decimal fractions.
Thus, 1/10 = 1 tenth = .1; 1/100 = 1 hundredth = .01;
88/100 = 88 hundredths = .88; 6/1000 = 6 thousandths = .006, etc.;
Conversion of a Decimal into Vulgar Fraction
Put 1 in the denominator under the decimal point and annex with it as many zeros as is the number of digits after the decimal point. Now, remove the decimal point and reduce the fraction to its lowest terms.
Thus, 0.25 = 25/100 = 1/4 ; 2.008 = 2008/1000 = 251/125.
Annexing Zeros and Removing Decimal Signs
Annexing zeros to the extreme right of a decimal fraction does not change its value. Thus, 0.8 = 0.80 = 0.800, etc.
If numerator and denominator of a fraction contain the same number of decimal places, then we remove the decimal sign.
Thus, 1.84/2.99 = 184/299 = 8/13.
Operations on Decimal Fractions
- Addition and Subtraction of Decimal Fractions: Arrange the provided numbers vertically, aligning their decimal points in a single column. This arrangement allows for the standard addition or subtraction of the numbers.
- Multiplication of a Decimal Fraction By a Power of 10: Shift the decimal point to the right by as many places as is the power of 10.
Thus, 5.9632 x 100 = 596.32; 0.073 x 10000 = 730. - Multiplication of Decimal Fractions: Multiply the provided numbers without considering the decimal point. After obtaining the product, place the decimal point in the result to have as many decimal places as the total sum of the decimal places in the original numbers.
Suppose we have to find the product (.2 x 0.02 x .002).
Now, 2 x 2 x 2 = 8. Sum of decimal places = (1 + 2 + 3) = 6.
.2 x .02 x .002 = .000008 - Dividing a Decimal Fraction By a Counting Number: Divide the given number by the specified counting number without taking the decimal point into account. Following the division, position the decimal point in the quotient to match the number of decimal places present in the original dividend.
Suppose we have to find the quotient (0.0204 Õ 17). Now, 204 Õ 17 = 12.
Dividend contains 4 places of decimal. So, 0.0204 Õ 17 = 0.0012 - Dividing a Decimal Fraction By a Decimal Fraction: Multiply both the dividend and the divisor by a suitable power of 10 to make divisor a whole number.
Now, proceed as above.
Thus, 0.00066/0.11 = 0.00066 x 100/0.11 x 100 = 0.066/11 = .006
Comparison of Fractions
Suppose some fractions are to be arranged in ascending or descending order of magnitude, then convert each one of the given fractions in the decimal form, and arrange them accordingly.
Let us to arrange the fractions 3/5, 6/7 and 7/9 in descending order.
Now, 3/5 = 0.6, 6/7 = 0.857, 7/9 = 0.777…
Since, 0.857 > 0.777… > 0.6. So, 6/7 > 7/9 > 3/5 .
Recurring Decimal
If in a decimal fraction, a figure or a set of figures is repeated continuously, then such a number is called a recurring decimal.
If a single figure is repeated, then it is expressed by putting a dot on it. If a set of figures is repeated, it is expressed by putting a bar on the set.
Thus, 1/3 = 0.333… = 0.3; 22/7 = 3.142857142857…. = 3.142857.
- Pure Recurring Decimal: A pure recurring decimal is a decimal fraction where the digits after the decimal point are repeated.
- Converting a Pure Recurring Decimal into Vulgar Fraction: Express a pure recurring decimal by writing its repeating digits once in the numerator and using a corresponding number of nines in the denominator. For example, 0.5 can be represented as 5/9, 0.53 as 53/99, and 0.067 as 67/999.
- Mixed Recurring Decimal: A mixed recurring decimal is characterized by a decimal fraction where some digits repeat while others do not. For instance, 0.1733333... can be simplified to 0.173.
Examples
Example 1: Evaluate 1082 using (a + b)2 formula.
(a) 11645
(b) 12547
(c) 11664
(d) 12745
Ans: (c)
Let’s write 108 as: 108 = 100 + 8
108 2 =(100 + 8) 2
Using the formula (a + b) 2 = a 2 + 2ab + b 2
108 2 = (100) 2 + 2(100)(8) + (8) 2
= 10000 + 1600 + 64
= 11664
Example 2: A recipe requires 3/4 cup of sugar to make 12 cookies. How much sugar would be needed to make 36 cookies?
(a) 2.25
(b) 2.5
(c) 3.5
(d) 4.5
Ans: (a)
To find the amount of sugar needed to make 36 cookies, we can set up a proportion based on the given information:
Sugar needed / Number of cookies = 3/4 cup / 12 cookies
Let’s solve for the unknown, which is the amount of sugar needed for 36 cookies:
Sugar needed / 36 = (3/4) cup / 12
Cross-multiplying gives us:
Sugar needed * 12 = 36 * (3/4)
Sugar needed * 12 = 108/4
Simplifying the right side:
Sugar needed * 12 = 27
Dividing both sides by 12:
Sugar needed = 27 / 12
Sugar needed = 2.25 cups
Therefore, to make 36 cookies, you would need 2.25 cups of sugar.
Example 3: If 47. 2506 = 4*A + 7/B + 2*C + 5/D + 6*E, then the value of 5*A + 3*B + 6*C + D + 3*E is:
(a) 53.6003
(b) 53.603
(c) 153.6003
(d) 213.003
Ans: (c)
4*A + 7/B + 2*C + 5/D + 6*E =47.2506
=> 4 * A + 7/B + 2 *C + 5/D + 6*E = 40 + 7 + 0.2 + 0.05 + 0.0006
Comparing the terms on both sides, we get :
4*A =40, 7/B = 7, 2*C = 0.2, 5/D = 0.05, 6*E = 0.0006
A = 10,
B = 1,
C = 0.1,
D = 100,
E = 0.0001.
5*A + 3*B + 6*C + D + 3*E =(5*10) + (3*1) + (6*0.1) +100 +(3*0.0001)
=50 + 3 + 0.6 + 100 + 0.003 = 153.6003.
Example 4: If 1.5x = 0.04y, then the value of 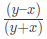 is:
is:
(a) 73/77
(b) 7.3/77
(c) 730/77
(d) 7300/77
Ans: (a)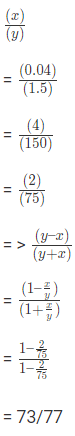
Example 5: Evaluate 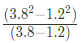
(a) 5.2
(b) 4.8
(c) 4
(d) 5
Ans: (d)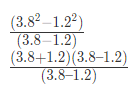
= 3.8 + 1.2 = 5
|
317 videos|290 docs|185 tests
|





















