Tips and Tricks: Harmonic Progressions | Quantitative Aptitude for SSC CGL PDF Download
HP tricks
One useful technique is to convert the HP into an AP of reciprocals. This can simplify calculations, as working with an AP might be more familiar and straightforward.
Harmonic Progression Tips and Tricks and Shortcuts
- For two numbers, if A, G and H are respectively the arithmetic, geometric and harmonic means, then A≥ G ≥ H
- Relationship between arithmetic, geometric, and harmonic means AM × HM = GM2
- Unless a = 1 and n = 1, the sum of a harmonic series will never be an integer. This is because at least one denominator of the progression is divisible by a prime number that does not divide any other denominator.
- Three consecutive numbers of a HP are:
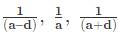
- Four consecutive numbers of a HP are:
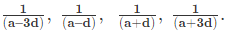
Type 1: Find nth term of series 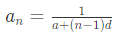
Example 1: Find the Middle term in this Harmonic series 4, a, 6
(a) 22/5
(b) 21/5
(c) 23/5
(d) 24/5
Ans: (d)
We know that, 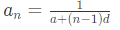
we know Inverse of HP is AP.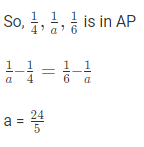
Example 2: Find the 8th term in the series 1/2, 1/4, 1/6 …….
(a) 1/20
(b) 1/14
(c) 1/16
(d) 1/18
Ans: (c)
We know that,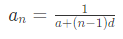
Convert the HP series in AP
We get 2, 4, 6,……
In the given series,
a (first term) = 2
d (common difference) = 2 …. (4 – 2)
Therefore, 8th term = t8 = a + (n - 1) d
t8 = 2 + (8– 1) 2
t8 = 2 + 7 x 2
t8 = 2 + 14
t8 = 16
Type 2: Find the Harmonic mean of the series 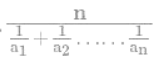
Example 1: Find the correct option for A, G, H for the elements 4 and 6 . where A is Arithmetic Mean, G is Geometric Mean & H is Harmonic Mean.
(a) A ≥ G ≥ H
(b) A < G > H
(c) A < G ≥ H
(d) A < G < H
Ans: (a)
Arithmetic mean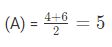
Geometric mean (G) = ( 4 × 6 )1/2 = 4.89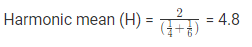
Hence it is shown that A ≥ G ≥ H
Example 2: If Harmonic Mean of two numbers is 8 and one of the number is 12 then Find Another Number.
(a) 2
(b) 4
(c) 6
(d) 8
Ans: (c)
We know that,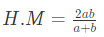
Let another number = b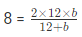
96 + 8b = 24b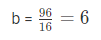
Another number = 6
Example 3: Find the harmonic mean (HM) of 8, 9, 6?
(a) 4.55
(b) 6.65
(c) 7.56
(d) 7.44
Ans: (d)
We know that,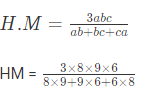
HM = 7.44
|
317 videos|294 docs|185 tests
|
FAQs on Tips and Tricks: Harmonic Progressions - Quantitative Aptitude for SSC CGL
| 1. What is a harmonic progression? |  |
| 2. How can harmonic progressions be useful in mathematics? |  |
| 3. What are some common examples of harmonic progressions? |  |
| 4. How can one determine the sum of a harmonic progression? |  |
| 5. Are there any shortcuts or tricks for working with harmonic progressions? |  |
















