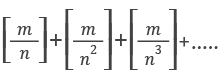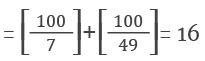Tips and Tricks: Number System | Quantitative Aptitude (Quant) - CAT PDF Download
| Table of contents |

|
| Introduction |

|
| 1. Number Properties |

|
| 2. Factorization Techniques |

|
| 3. Divisibility and Cyclicity |

|
| 4. Remainder Concepts |

|
| 5. HCF and LCM |

|
Introduction
The Number System is a crucial topic in the CAT Quantitative Section. It is extensive and includes numerous tricks and shortcut formulas that enable students to solve questions quickly.
The most frequently tested concepts in the CAT exam from this topic include:
1. Number properties
2. Factorization techniques
3. Divisibility rules
4. Remainder concepts
5. HCF and LCM
We will cover short tricks of each of the topics listed above and also include practice questions for better understanding.
1. Number Properties
(i) For calculating the number of zeroes at the end of the factorial of a number, you should divide the number by 5, the quotient obtained is again divided by 5 and so on till the last quotient obtained is smaller than 5. The sum of all the quotients is the number of 5s, which then becomes the number of zeroes in the given number.(ii) The digital root of a number is the sum of the digits, over and over again, till it becomes a single-digit number. For example, the digital root of 87984 will be 8 + 7 + 9 + 8 + 4 ⇒ 36 = 3 + 6 ⇒ 9.
(iii) When the concept of the Euler number is used and the dividend and divisor happen to be co-prime, the remainder questions become very easy.
(iv) The product of 3 consecutive natural numbers is divisible by 6.
(v) The product of 3 consecutive natural numbers, the first of which is an even number, is divisible by 24.
(vi) The sum of a two-digit number and a number formed by reversing its digits is divisible by 11.
E.g. 28 + 82 = 110, this is divisible by 11. At the same time, the difference between those numbers will be divisible by 9. e.g. 82 – 28 = 54, this is divisible by 9.
(vii) Σn = n(n+1)/2, Σn is the sum of the first n natural numbers.
(viii) Σn² = n(n+1)(n+2)/6, Σn² is the sum of the first n perfect squares.
(ix) Σn³ = n²(n+1)²/4 = (Σn)², Σn³ is the sum of the first n perfect cubes.
(x) xⁿ + yⁿ = (x + y) (xⁿ⁻¹ - xⁿ⁻²y + xⁿ⁻³y² - ... + yⁿ⁻¹) when n is odd.
Therefore, when n is odd, xⁿ + yⁿ is divisible by x + y.
e.g. 3³ + 2³ = 35 and is divisible by 5, which is (3 + 2).
(xi) xⁿ - yⁿ = (x + y) (xⁿ⁻¹ - xⁿ⁻²y + ... yⁿ⁻¹) when n is even.
Therefore, when n is even, xⁿ - yⁿ is divisible by x + y.
e.g. 7² - 3² = 40, is divisible by 10, which is (7 + 3).
(xii) xⁿ - yⁿ = (x - y) (xⁿ⁻¹ + xⁿ⁻²y + ... + yⁿ⁻¹) for both odd and even n.
Therefore, xⁿ - yⁿ is divisible by x - y.
For example, 9⁴ - 2⁴ = 6545, which is divisible by 7, which is (9 - 2).
Questions Based on Number Properties
Example 1: If N = (18n² + 9n + 8)/n; where N belongs to integer. How many integral solutions of N are possible?
Sol: The given expression can be broken as: 18n²/n + 9n/n + 8/n.
This gives us: 18n + 9 + 8/n. Now we can see that whatever the value of ‘n’, 18n + 9 will always give an integral value.Therefore, it now depends upon 8/n only ⇒ n can have any integral value, which is a factor of 8.
The integers which will satisfy this condition are ±1, ±2, ±4, ±8. Thus, in total, n can take 8 values.
Example 2: The digits of the number (4)24 are summed up continually till a single digit number is obtained. What is that number?
Sol: 43 = 64.
Digital sum of 64 is = 1. 424 = 43 × 43 × 43 …× 43 (8 times).
⇒Digital sums on both sides will be the same.
digital sum of 424 = digital sum of 1 × 1 × 1 × 1… (8 times) = 1
Example 3: If x and y are positive integers and x2 – y2 = 101, find the value of x2 + y2.
(a) 5050
(b) 5150
(c) 5101
(d) None of these
Sol: x2 – y2 = (x + y)(x – y) = 101.
But 101 is a prime number and cannot be written as product of two numbers unless one of the numbers is 1 and the other is 101 itself. Hence, x + y = 101 and x – y = 1.
After solving we get, x = 51, y = 50.
⇒ x2 + y2 = 512 + 502 = 5101.
2. Factorization Techniques
(i) Number of factors
If we have to find the number of factors of any number say N, then we should follow the below steps:
Step 1: Prime factorize N = pᵃ × qᵇ × rᶜ × ...
Step 2: The number of factors of N = (a+1)(b+1)(c+1)...
(ii) Sum of factors
To find the sum of all the factors of a number (say N), we follow the below two steps:
Step 1: Prime factorize N = pᵃ × qᵇ × rᶜ × ...
Step 2: Sum of factors = ( (p - 1)(a+1) / (p - 1) ) × ( (q(b+1) - 1) / (q - 1) ) × ( (r(c+1) - 1) / (r - 1) ) ...
(iii) Product of Factors
To find the product of all the factors of a number (say N), we follow the below three steps:
Step 1: Prime factorize N = pᵃ × qᵇ × rᶜ × ...
Step 2: Let the number of factors of N be x. Therefore, x = (a+1)(b+1)(c+1)...
Step 3: Product of factors = N(x/2)
Let us take an example to understand the working of the above formulas.
(iv) Number of odd and even factors
If a number N can be prime factorized as N = 2a × P₁b × P₂c, (Where P₁, P₂, P₃ and so on are distinct prime numbers apart from 2) then the
- Number of odd factors = (b+1) × (c+1)x ..
- Number of even factors = Total number of factors - Number of odd factors
Did You Know?
Euler's theorem
If M & N are co-prime to each other than remainder when Mϕ(N) is divided by N is 1.
Highest power of n in m! is
Example: Highest power of 7 in 100!
Questions Based on Factorization Techniques
Example 1: Find the number of factors, the sum of factors, and the product of factors of 1800.
Sol:
Prime factorization of 1800 = 2³ × 3² × 5²
Number of factors 1800 = (3+1)(2+1)(2+1) = 36
= ( (23+1- 1) / (2 - 1) ) × ( (32+1 1) / (3 - 1) ) × ( (52+1 - 1) / (5 - 1) )
= 15 × 4 × 31 = 1860
Product of Factors of 1800 = 1800(36/2) = 180018
Example 2: Find the number of Even and Odd factors of 1200.
Sol:
Prime factorization of 1200 = 24 × 31 × 52
We know the fact that all the factors of 1200 will be in the form of 2a × 3b × 5c.
Where a will range from 0 to 4, b from 0 to 1, and c from 0 to 2. However, it is quite evident that any factor which has 2 as one of the prime factors is always even. Similarly, your factors will not have 2 as its prime factor.
Therefore, for Odd factors, the exponent of 2 i.e., a has to be 0 always.
Or, the number of ways using 2 for making the combination is 1, i.e., 2⁰.
Also, the number of values that the exponent of 3 and 5, i.e., b and c can take are 2 and 3 respectively.
Hence the number of odd factors of 1200 = 1 × 2 × 3 = 6.
Extending the logic, we can say that for a factor to be Even, it must contain 2 at least once.
So, the number of values a, b, and c can take are 4, 2, and 3 respectively.
Therefore, the total number of even factors of 1200 = 4 × 2 × 3 = 24.
Example 3: Find the number of factors which are perfect squares of 10800.
Sol: Prime factorization of 10800 = 24 × 33 × 52
If we prime factorize any number which is a perfect square, we would observe that in all cases the exponent of all the prime factors of the number has to be even only.
For example, 36 is a perfect square 36 = 2² × 3². Here we can see that the exponent of both 2 and 3 are even.
Again, any factor of 10800 will be in the form of 2a× 3b × 5c. For the factors to be perfect squares, all the values a, b, and c have to be even only.
Or, the possible values which a can take = 0, 2, 4, i.e. 3 values only.
Similarly, b can take 0, 2, i.e. 2 values and c can take 0, 2, i.e. 2 values.
Therefore, the different combinations we can have = 3 × 2 × 2 = 12.Hence, 10800 has 12 factors which are perfect squares.
3. Divisibility and Cyclicity
Divisibility
(i) Divisibility by 2: Last digit divisible by 2(ii) Divisibility by 4: Last two digits divisible by 4
(iii) Divisibility by 8: Last three digits divisible by 8
(iv) Divisibility by 16: Last four digit divisible by 16
(v) Divisibility by 3: Sum of digits divisible by 3
(vi) Divisibility by 9: Sum of digits divisible by 9
(vii) Divisibility by 27: Sum of blocks of 3 (taken right to left) divisible by 27
(viii) Divisibility by 7: Remove the last digit, double it and subtract it from the truncated original number, check if the number is divisible by
(ix) Divisibility by 11: (sum of odd digits) - (sum of even digits) should be 0 or divisible by 11
Divisibility Properties
For composite divisors, check if the number is divisible by the factors individually.
- Hence to check if a number is divisible by 6 it must be divisible by 2 and 3.
- The equation an - bn is always divisible by a-b. If n is even it is divisible by a + b. If n is odd it is not divisible by a + b.
- The equation an + bn is divisible by a+b if n is odd. If n is even it is not divisible by a+b.
- Converting from decimal to base b. Let R1 + R2 .. be the remainder left after repeatedly dividing the number with b. Hence, the number in base b is given by R2 R1.
- Converting from base b to decimal - multiply each digit of the number with a power of b starting with the rightmost digit and b 0 .
- A decimal number is divisible by b-1 only if the sum of the digits of the number when written in base b are divisible by b-1.
Cyclicity
To find the last digit of a n find the cyclicity of a. For Ex. if a=2, we see that- 21 = 2
- 22 = 4
- 23 = 8
- 24 = 16
- 25 = 32
Hence, the last digit of 2 repeats after every 4th power. Hence cyclicity of 2 = 4. Hence if we have to find the last digit of an, The steps are:
- (a + b)(a — b) = (a2 — b2)
- (a + b)2 = (a2 + b2 + 2 ab)
- (a — b)2 = (a2 + b2 — 2ab)
- (a + b + c)2 = (a2 + b2 + 2(ab + be + ca))
- (a + b + c)2= (a2 + b2 + 2 (ab + bc + ca))
- (a3 + b3) = (a + b) (a2 — ab + b2)
- (a3 + b3) = (a + b) (a2 — ab + b2)
- (a3 + b3) = (a + b) (a2 — ab + b2)
- (a3 + b3 + c3 — 3abc) = (a + b) (a2 + b2 + c2 — ab — bc — ac)
- When a + b + c = 0, then a3 + b3 + c3 = 3abc
Questions Based on Divisibilty and Cyclicity
Example 1: What is the number of even factors of 36000 which are divisible by 9 but not by 36?
(a)20
(b) 4
(c) 10
(d) 12
Sol: 36000 = 2⁵ × 3² × 5³
Since we are talking of even factors, there must be at least one 2 in the required factors.
Since the number is divisible by 9, we must have both the threes.
We cannot have more than 1 two as it will make the number divisible by 36.
So we have 1 way of choosing 2, 1 way of choosing 3, 4 ways of choosing 5.
Thus the required number of factors are
1 × 1 × 4 = 4
Example 2: The number A39K2 is completely divisible by both 8 and 11. Here both A and K are single digit natural numbers.
Which of the following is a possible value of A + K?
(a) 8
(b) 10
(c) 12
(d) 14
Sol: The number is divisible by 11, so the difference between the sum of the digits at the odd places and the digits at the even places is either 0 or a multiple of 11.
Let the difference be a 0, so
11 + A = 3 + K
=> K - A = 8, the only possible value is 9,1
Now we have to check if it satisfies the divisibility by 8 test.
K = 9 makes the last 3 digits 992. This is divisible by 8.
Let’s check for other cases when the difference is 11
11 + A - 3 - K = 11 => A - K = 3
The possible values in this case are (9,6), (8,5), (7,4), (6,3), (5,2), (4,1)
Among these cases only (8,5) and (4,1) will be divisible by 8.So the possible values of sum are
13, 5 and 10
Now difference between the sum of odd and even places cannot be 22
11 + A - 3 - K = 22 => A - K = 14
Since both A and K are single digit natural numbers, this is not possible.
Thus the only possible values of sum are 5, 10 and 13.
In the given options only 10 is there. So it is the correct choice.
Example 3: If m and n are natural numbers such that n > 1, and mⁿ = 225 × 340, then m - n equals
(a) 209932
(b) 209937
(c) 209942
() 209947
Sol: We must bring the right-hand side in the form so that everything has the same power.
25 has factors 1, 5 and 25
The only common factor 40 and 25 have is 5 (other than 1 of course, which does not work)
So the right-hand side can be rewritten as (2⁵)⁵ × (3⁸)⁵
(32 × 81 × 81)⁵
(209952)⁵
Giving the value of m - n as 209952 - 5 = 209947
Therefore, Option D is the correct answer.
4. Remainder Concepts
(i) To find the number of zeroes in n! find the highest power of 5 in n!
(ii) If all possible permutations of n distinct digits are added together the sum = (n-1)! x (sum of n digits) x (11111... n times)
(iii) If the number can be represented as N = apx bqxcr... then number of factors the is (p+1) x (q+1)x (r+1)
(iv) Sum of the factors = 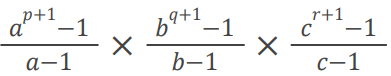
(v) If the number of factors are odd then N is a perfect square.
(vi) If there are n factors, then the number of pairs of factors would be n/2.
(vii) If N is a perfect square then number of pairs (including the square root) is (n+1)/2.
(viii) If the number can be expressed as N = 2p x aq x br ... where the power of 2 is p and a, b are prime numbers. Then the number of even factors of N = p (1+q) (1+r)... The number of odd factors of N = (1+q) (1+r)…
(ix) Number of positive integral solutions of the equation x2 + y2 = k is given by
Total number of factors of k/2 (If k is odd but not a perfect square)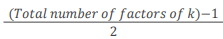 (If k is odd and a perfect square)
(If k is odd and a perfect square)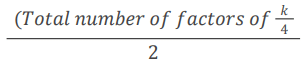 (If k is even and not a perfect square)
(If k is even and not a perfect square)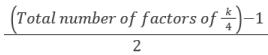 (If it is even and a perfect square)
(If it is even and a perfect square)
(x) Number of digits in ab = [ b logm (a) ] + 1; where m is the base of the number and [.] denotes the greatest integer function.
(xi) Even a number which is not a multiple of 4, can never be expressed as a difference of 2 perfect squares.
(xii)The sum of first n odd numbers is n2.
(xiii)The sum of first n even numbers is n(n+1).
(xiv) The product of the factors of N is given by Na/2, where a is the number of factors.
(xv) The last two digits of a2, (50 - a)2, (50 + a)2, (100 - a2). . . . . are the same.
(xvi) If the number is written as 210n.
(xvii) When n is odd, the last 2 digits are 24.
(xviii) When n is even, the last 2 digits are 76.
Did You Know?
1. Fermat's Theorem: Remainder of a(p-1) when divided by p is 1, where p is a prime.
2. Wilson's Theorem: Remainder when (p-1)! is divided by p is (p-1) where p is a prime
3. Remainder Theorem
If a, b, c are the prime factors of N such that N= ap x bqx cr Then the number o f numbers less than N and co-prime to N is ϕ(N)= N (1 - 1/a) (1 - 1/b) (1 - 1/c).
This function is known as the Euler's totient function.
Questions Based on Remainders
Example 1: What is the remainder when 123 × 124 × 125 is divided by 9.
Sol: Remainder obtained when 123 is divided by 9 = -3
Remainder obtained when 124 is divided by 9 = -2
Remainder obtained when 123 is divided by 9 = -1
Final remainder = (-3)(-2)(-1) = -6. The required positive remainder = 9-6 = 3.
Example 2: What is the remainder when the product 1998 × 1999 × 2000 is divided by 7?
(a) 0
(b) 1
(c) 2
(d) 4
Sol: The remainders when 1998, 1999, and 2000 are divided by 7 are 3, 4, and 5 respectively.
Hence the final remainder is the remainder when the product 3 × 4 × 5 = 60 is divided by 7.
Therefore, remainder = 4
Example 3: What is the remainder when 3444 + 4333 is divided by 5?
Sol: The dividend is in the form ax + by. We need to change it into the form an + bn.
3444 + 4333 = (34)111 + (43)111.
Now (34)111 + (43)111 will be divisible by 34 + 43 = 81 + 64 = 145.
Since the number is divisible by 145 it will certainly be divisible by 5.
Hence, the remainder is 0.
5. HCF and LCM
(i) A x B = H.C.F.(A,B) x L.C.M.(A,B)
(ii) HCF of fractions = 
(iii) LCM of fractions =
(iv) Remainders based on HCF and LCM
- The greatest number that will divide A, B, and C, leaving remainders p, q, and r, respectively, is the HCF of (A-p), (B-q), and (C-r).
- The lowest number that is divisible by A, B, and C, leaving the same remainder “r” in each case is LCM of (A, B and C) + r.
- The greatest number that will divide p, q and r leaving the same remainder in each case, then required number = HCF of the absolute values of (p-q), (q-r), and (r-p).
(v) HCF of the numbers of the type (am -1) and (an - 1)
HCF of the numbers of the type (am -1) and (an - 1)
Step 1: Take HCF of a and b
Step 2: The required HCF = 2HCF(a,b) - 1
Did You Know ?
1. Number of zeroes in an expression
- Zeroes are formed by a combination of 2 × 5.
- Hence, the number of zeroes will depend on the number of pairs of 2’s and 5’s that can be formed.
2. Finding the number of zeroes in a factorial value
- Method 1: Suppose you had to find the number of zeroes in 6!. 6! = 6 × 5 × 4 × 3 × 2 × 1 = (3 × 2) × (5) × (2 × 2) × (3) × (2) × (1).
Counting the number of 5 will give the answer.- Method 2 : For finding the zeroes in 6! we use
So we get 1 as the answer as all divisions after the first term in the series are in decimals which we ignore.
Questions Based on HCF and LCM
Example 1: Find the HCF of 2100– 1 and 2120– 1
(a) 220−1
(b) 210−1
(c) 240−1
(d) 1
Sol: 2100– 1 = (220)5- 1 ⇒ divisible by 220 - 1 (an- bn is always divisible by a - b)
Similarly, 2120– 1 = (220)6- 1 ⇒ divisible by 220 - 1 (an- bn is always divisible by a - b)
⇒ HCF = 220 - 1
Example 2: For how many ordered pairs (a, b) of natural numbers is the LCM of a and b is 23571113?
Sol: Let's solve for the powers of 2.
One of the numbers will have 23 in it, as the LCM has 23.
Now the other number can have the powers of 2 as 20, 21, 22, and 23. Therefore, number of pairs will be 4: (23, 20), (23, 21), (23, 22), and (23, 23) and the number of ordered pairs will be 2 × 4 - 1 = 7 (we cannot count the pair (23, 23) twice.
Similarly ordered pairs for powers of 5 = 2 × 8 - 1 = 15.
Number of ordered pairs for powers of 7 = 2 × 14 - 1 = 27.
Total ordered pairs (a, b) = 7 × 15 × 27 = 2835
Example 3: Find the lowest number which gives a remainder of 5 when divided by any of the numbers 6, 7, and 8.
Sol: The LCM of 6, 7 and 8 is 168. Hence, 168 is divisible by 6, 7 and 8.
Therefore, 168 + 5 = 173 will give a remainder of 5 when divided by these numbers.
|
196 videos|217 docs|103 tests
|
FAQs on Tips and Tricks: Number System - Quantitative Aptitude (Quant) - CAT
| 1. What is the difference between HCF and LCM? |  |
| 2. How can I identify prime and composite numbers? |  |
| 3. What are some important properties of prime numbers? |  |
| 4. What are the key theorems related to prime numbers? |  |
| 5. How does the concept of divisibility apply to HCF and LCM? |  |