Tips and Tricks: Squaring | Improve Your Calculations: Vedic Maths (English) - Class 6 PDF Download
| Table of contents |

|
| Square of numbers ending in 5 |

|
| Squaring numbers above 50 |

|
| Squaring numbers near base |

|
| Squaring numbers near sub-base |

|
| General method of squaring |

|
| Algebraic Squaring |

|
Square of numbers ending in 5
Sutra: ‘By one more than previous one”
Example: 75 × 75 or 752
As explained earlier in the chapter of multiplication we simply multiply 7 by the next number i.e. 8 to get 56 which forms first part of answer and the last part is simply 25 = (5)2. So, 75 × 75 = 5625
This method is applicable to numbers of any size.
Example 2: 6052
60 × 61 = 3660 and 52 = 25
∴ 6052 = 366025
Square of numbers with decimals ending in 5
Example 3: (7.5)2
7 × 8 = 56, (0.52) = 0.25
(7.5)2 = 56.25 (Similar to above example but with decimal)
Squaring numbers above 50
Example: 522
Step 1: First part is calculated as 52 + 2 = 25 + 2 = 27
Step 2: Last part is calculated as (2)2 = 04 (two digits)
∴ 522 = 2704
Squaring numbers below 50
Example: 482
Step 1: First part of answer calculated as: 52 – 2 = 25 – 2 = 23
Step 2: second part is calculated as: 22 = 04
∴ 482 = 2304
Squaring numbers near base
Example: 10042
Step 1: For first part add 1004and 04 to get 1008
Step 2: For second part 42 = 16 = 016 (as, base is 1000 a three digit no.)
∴ (1004)2 = 1008016
Squaring numbers near sub-base
Example: (302)2
Step 1: For first part = 3 (302 + 02) = 3 × 304 = 912 [Here sub – base is 300 so multiply by 3]
Step 2: For second part = 22 = 04
∴ (302)2 = 91204
General method of squaring
The Duplex
Sutra: “Single digit square, pair multiply and double” we will use the term duplex,` D’ as follows:
For 1 figure(or digit) Duplex is its square e.g. D(4) = 42 = 16
For 2 digits Duplex is twice of the product e.g. D(34) = 2 (3 x 4) = 24
For 3 digit number: e.g. (341)2
D(3) = 32 = 9
D (34) = 2 (3 × 4) = 24
D (341) = 2 (3 × 1 ) + 42 = 6 + 16 = 22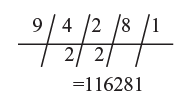
D (41 ) = 2 (4 × 1 ) = 8
D (1) = 12 = 1
∴ (341)2 = 116281
Algebraic Squaring
Above method is applicable for squaring algebraic expressions:
Example 1: (x + 5)2
D (x) = x2 D(x + 5) = 2 (x × 5) = 10x
D (5) = 52 = 25
∴ (x + 5)2 = x2 + 10x + 25
Example: (x – 3y)2
D (x)= x2
D(x – 3y) = 2 (x) × – 3y) = – 6xy
D(–3y ) = (–3y)2 = 9y2
∴ (x – 3y)2 = x2 – 6xy + 9y2
|
36 videos|31 docs|3 tests
|
|
36 videos|31 docs|3 tests
|

|
Explore Courses for Class 6 exam
|

|
















