Tools & Postulates of Quantum Mechanics: Assignment | Modern Physics PDF Download
Q.1. Consider the Gaussian probability distribution where -∞ < x < ∞ where A,a and λ are positive real constants.
where -∞ < x < ∞ where A,a and λ are positive real constants.
(a) Determine A such that f(x) is probability density
(b) Find 〈x〉 ,〈x2〉 and σ = Δx
(c) Sketch the graph of f(x)
(a)
(c)
Q.2. If |ϕ1〉 and |ϕ2〉 be two orthonormal state vectors such that A = |ϕ1〉 〈ϕ2| + |ϕ2〉 〈ϕ1| then
(a) Prove that A is Hermitian
(b) Find the value of A2.
For A to be a projection operator, A should be Hermitian and A2 should be equal to A. The Hermitian adjoint of |ϕ1〉 〈ϕ2| is |ϕ2〉 〈ϕ1| and that of |ϕ2〉 〈ϕ1| is |ϕ1〉 〈ϕ2|. So
Hence A is Hermitian.
Now,
Since |ϕ1〉 and 〈ϕ2| are orthonormal,
Q.3. The needle on a broken car speedometer is free to swing, and bounces perfectly of the pins at either end, so that if you give it a flick it is equally likely to come to rest at any angle between 0 and π
(a) What is the probability density, f (θ)?
(b) Compute 〈θ〉, 〈θ2〉 and σ = Δθ, for this distribution
f(θ) = A ,0 < θ < π
Q.4. (a) Find the Eigen State of momentum operator 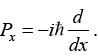 If eigen value is λ by relation Pxϕ = λ/ϕ where λ/ℏ = k.
If eigen value is λ by relation Pxϕ = λ/ϕ where λ/ℏ = k.
(b) Expand the wave function ψ(x) = A sin kx sin 2kx in basis of Eigen functions of momentum operator Px
Pxϕ = λ/ϕ where λ/ℏ = k.
Case 1: If l is positive
Case 2: If l is negative
(b) Expand the function ψ(x) = A sin kx sin 2kx as a linear combination of eigenfunctions of the momentum operator Px.
Q.5. Consider the function ψ(x, t) = Ae-λ|x|e-ωt -∞ < x < ∞, where λ and ω are are constant. Find the value of A such that ψ (x, t) is normalized.
(a) ψ(x, t) = Ae-λ|x|e-ωt
Q.6. Prove that operator  is Hermitian but Dx = d/dx is not Hermitian.
is Hermitian but Dx = d/dx is not Hermitian.
The given operator
is the same as Px . Let ψ1 (x) and ψ2 (x) be two arbitrary
functions.
Integrating by parts, this is equal to
For the wave function to be square integrable, it must go to zero as x goes to -∞ or +∞.Thus, the first term in the square bracket is zero. So,
From (i) and (ii), 〈ψ1|Pxψ2〉 = 〈Pxψ1|ψ2〉
Henceis Hermitian. Similar calculation with A = d/dx will give,
Hence, 〈ψ1|Aψ2〉 ≠ 〈Aψ1|ψ2〉 and so, A = d/dx is not Hermitian.
Q.7.
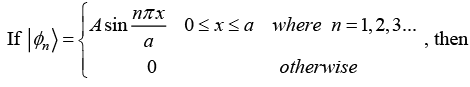
(a) Find the value of A such that |ϕn〉 is normalized
(b) 〈ϕm|ϕn〉 = δm,n
(c) If H operator is defined as 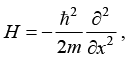 then prove that the matrix element
then prove that the matrix element
Q.8. Show that operator O = (1 + i) AB + (1 - i) BA is Hermitian if A and B is Hermitian.
[(1 + i) AB + (1 - i) BA]† = [(1 + i)AB]† + [(1 - i)BA]†
= (1+ i)* (AB)† + (1 - i)* (BA)†
= (1 - i)* B†A† + (1 + i)* A†B† if A and B is hermitian.
= (1 - i) BA + (1 + i)AB
(1 + i) AB + (1 - i)BA
Thus the given operator is Hermitian
Q.9. (a) If ϕ1(θ, ϕ) = A find the value of A such that ϕ1 (θ, ϕ) is normalized.
(b) Prove that 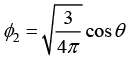 is orthogonal to ϕ1
is orthogonal to ϕ1
The wave function ϕ1 (θ, ϕ) = A is defined in spherical symmetry variable is solid angle
Q.10. Using Bohr-Somerfield theory, find the energy for a particle of mass m is confined in potential V(x) = k|x|.
Q.11.
(a) Find normalization constant A, B, C for ket |ϕ1〉 |ϕ2〉 |ϕ3〉
(b) Prove that |ϕ1〉, |ϕ2〉 and |ϕ3〉 are orthogonal
(c) Check whether |ϕ1〉, |ϕ2〉 and |ϕ3〉are linearly independent or not.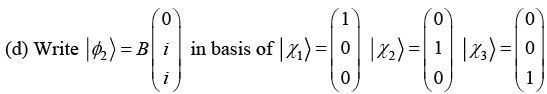
(e) 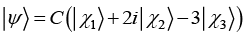 then find value of C such that |ψ〉 is normalized
then find value of C such that |ψ〉 is normalized
(f) If operator A is defined as 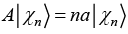 where n = 1, 2, 3... then find value of A|ψ〉
where n = 1, 2, 3... then find value of A|ψ〉
(g) If operator A is defined as 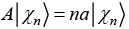 where n = 1, 2, 3... then find value of
where n = 1, 2, 3... then find value of 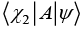
(h) If operator A is defined as 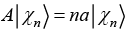 where n = 1, 2, 3... then find value of 〈ψ|A|ψ〉
where n = 1, 2, 3... then find value of 〈ψ|A|ψ〉
then 〈ϕ1| = A* (1 0 0), 〈ϕ2| = B* (0 -i -i), 〈ϕ2| = C* (0 -i -i)
c1 = 0 c2 + c3 = 0 and c2 - c3 = 0 ⇒ c1 = 0, c2 = 0, c3 = 0
So |ϕ1〉, |ϕ2〉 and |ϕ3〉 are linearly independent
Q.12. If Hamiltonian of system is 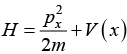 then Find commutation [H, x] and [[H, x], x]
then Find commutation [H, x] and [[H, x], x]
As, H = p2 / 2m + V(x)
Q.13. Let |θ1〉 and |θ2〉 be two eigenfunction of Hamiltonian operator with eigen value E0 and 4E0 respectively. The wave function of the particle at time t = 0 is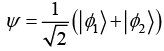 which is also eigen function of operator A with eigen value a0. The operator A is associated with observable a.
which is also eigen function of operator A with eigen value a0. The operator A is associated with observable a.
(a) If H is measured on state ψ at t = 0 what is measurement with what probability.
(b) If A is measured on state ψ at t = 0 what is probability to get eigen value a0.
(c) If A is measured on state ψ at t = t what is probability to get eigen value a0.
(d) Find error in measurement of energy ie ΔE
(e) Find ΔE.Δt
H|θ1〉 = E0|θ1〉 and H|θ2〉 = 4E0 |θ2〉
H is measured on state ψ at t = 0 what is measurement is eigen value E0 and 4E0
(b) A|ψ〉 = a0|ψ〉
Probability of getting a0 on state ψ at t = 0
Q.14. Consider the operator 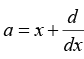 acting on smooth function of x. find the commutation [α , cos x]
acting on smooth function of x. find the commutation [α , cos x]
[a, cos x]ψ(x) = -sin xψ [a, cos x] = -sin x
Q.15. Consider the two lowest normalized energy eigenfunctions ψ0 (x) and y1 (x) of a one dimensional system. They satisfy ψ0 (x) = ψ*0 (x) and ψ1(x) = 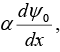 where α is a real constant. The expectation value of the momentum operator in the state ψ1 is
where α is a real constant. The expectation value of the momentum operator in the state ψ1 is
Integrate by parts
Q.16. (a) using Heisenberg uncertainty principle estimate the minimum possible energy of linear Harmonic oscillator of mass m. The potential for such a particle is v(x) = (mω2x2)/2/
(b) when an electron is accelerated through a potential difference V, its de Broglie Wave length is α/√V for non relativistic speed. If λ and V represent numerical values in Angstrom and Volt, find the numerical value of α.
(a) In order to have an uncertainty of Δpx, the value of the momentum itself should have at least a value comparable to Δpx. You cannot have an uncertainty of 5 units if the value never exceeds 2 units. So we assume that p ≈ Δpx. Similarly x ≈ Δx. The expression for energy is
From uncertainty principle,As we are looking for the lowest energy, let us write Δpx = ℏ/2Δx ,
For E to be minimum, dE/d(Δx) should be zero. This gives,
(b) As an electron is accelerated through a potential difference V, its potential energy is decreased by eV. The kinetic energy gained is equal to this value. So,eV = mv2 / 2 = p2 / (2m)
or,
de broglie wavelength is
For an electron, h2/2m = 1.5eV nm2.
If V is put in volts, the energy eV is the same as V electronvolts. Cancelling the unit eV from the numerator and the denominator,
So, α = 12.25.
Q.17. Consider a system whose initial state 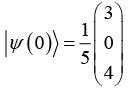 and Hamiltonian is defined as
and Hamiltonian is defined as 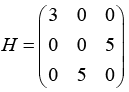
(a) If a measurement of energy is carried out what values would be obtained with what probabilities?
(b) Find the state of system at later time t,
(c) Find the average value of energy at time t = 0.
(d) Find the average value of energy at time t = t.
(a) A measurement of the energy yields the values E1 = -5 , E2 = 3 , E3 = 5 ; the respective (orthonormal) eigenvectors of these values are
The probabilities of finding the values E1 = -5 , E2 = 3 , E3 = 5 are given by
(b) To find |ψ(t)〉 we need to expand |ψ(0)〉 in terms of the eigenvectors
Hence,
(c) We can calculate the energy at time t = 0 in three quite different ways. The first method uses the bra-ket notation. Since 〈ψ(0)|ψ(0)〉 = 1, 〈ϕn)|ϕm〉 = δnm and sincewe have
The second method uses matrix algebra:
The energy at time t is
As expected E (t) = E (0) since
Q.18. A Particle of mass m is subjected to the potential energy 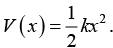 At a particular time it has wave function
At a particular time it has wave function 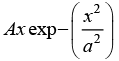 and identified as energy eigen function with definite total mechanical energy .find the value of a.
and identified as energy eigen function with definite total mechanical energy .find the value of a.
The operator corresponding to the total mechanical energy is
If particle has definite value of the total mechanical energy, its wave function should be an eigenfunction of H, that is,
Hψ(x) = λψ where λ is independent of x
If Hψ(x) has to have the same functional form as ψ(x), one should not have theterm. So,
or
|
37 videos|16 docs|19 tests
|
FAQs on Tools & Postulates of Quantum Mechanics: Assignment - Modern Physics
| 1. What are the fundamental tools of quantum mechanics? |  |
| 2. What are the postulates of quantum mechanics? |  |
| 3. How does the Schrödinger equation relate to quantum mechanics? |  |
| 4. What is the significance of wave functions in quantum mechanics? |  |
| 5. How do operators and observables relate to measurements in quantum mechanics? |  |

|
Explore Courses for Physics exam
|

|


















 is the same as Px . Let ψ1 (x) and ψ2 (x) be two arbitrary
is the same as Px . Let ψ1 (x) and ψ2 (x) be two arbitrary 





 is Hermitian. Similar calculation with A = d/dx will give,
is Hermitian. Similar calculation with A = d/dx will give,





























 H|θ1〉 = E0|θ1〉 and H|θ2〉 = 4E0 |θ2〉
H|θ1〉 = E0|θ1〉 and H|θ2〉 = 4E0 |θ2〉













 As we are looking for the lowest energy, let us write Δpx = ℏ/2Δx ,
As we are looking for the lowest energy, let us write Δpx = ℏ/2Δx , 









 we have
we have




 If particle has definite value of the total mechanical energy, its wave function should be an eigenfunction of H, that is,
If particle has definite value of the total mechanical energy, its wave function should be an eigenfunction of H, that is,

 term. So,
term. So, 


















