Top Puzzle 9: The Seven Bridge Problem | Puzzles for Interview - Interview Preparation PDF Download
Problem Statement
The Seven Bridges Problem, also known as the Königsberg Bridge Problem, is a mathematical puzzle that originated in the 18th century in the Prussian city of Königsberg (now Kaliningrad, Russia). The city was divided by the Pregel River, which had seven bridges connecting its various landmasses, including two large islands. The challenge was to find a path that crossed each of the seven bridges exactly once and returned to the starting point.
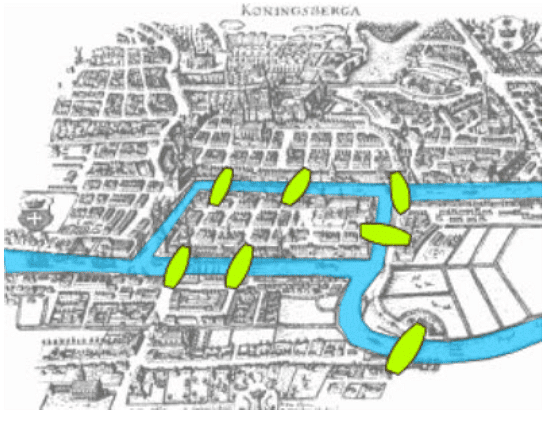
Solution
The Seven Bridges Problem was solved by Swiss mathematician Leonhard Euler in 1736. Instead of considering the bridges and landmasses themselves, Euler looked at the problem from an abstract point of view. He represented the landmasses as nodes (vertices) and the bridges as connections (edges) between the nodes. This allowed him to create a branch of mathematics known as graph theory.
Euler realized that for a walk to exist that crossed each bridge exactly once and returned to the starting point, each node must have an even number of edges. This is because, for each edge a person enters a node, they must also leave the node through a different edge. Having an even number of edges ensures that this is possible. This type of walk is called an Eulerian circuit.
In the case of the Seven Bridges Problem, Euler found that there were four nodes (landmasses) and seven edges (bridges). He discovered that each node had an odd number of edges. Therefore, it was impossible to find a walk that crossed each bridge exactly once and returned to the starting point.
Conclusion
The Seven Bridges Problem played a pivotal role in the development of graph theory and paved the way for further advancements in mathematics. Euler's innovative approach to solving the problem demonstrated the power of abstraction in problem-solving. His work on this problem established a new mathematical field and provided a framework for solving similar problems in the future.
The conclusion of the Seven Bridges Problem is that it is impossible to find a walk that crosses each bridge exactly once and returns to the starting point because each landmass (node) has an odd number of bridges (edges) connecting it to other landmasses. This counterintuitive result highlights the importance of logical reasoning and creative problem-solving in mathematics.
















