Topological Sorting | Algorithms - Computer Science Engineering (CSE) PDF Download
Introduction
Topological sorting for Directed Acyclic Graph (DAG) is a linear ordering of vertices such that for every directed edge u v, vertex u comes before v in the ordering. Topological Sorting for a graph is not possible if the graph is not a DAG.
For example, a topological sorting of the following graph is “5 4 2 3 1 0”. There can be more than one topological sorting for a graph. For example, another topological sorting of the following graph is “4 5 2 3 1 0”. The first vertex in topological sorting is always a vertex with in-degree as 0 (a vertex with no incoming edges).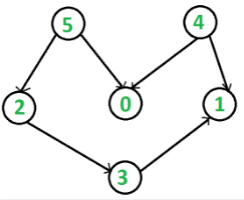
Topological Sorting vs Depth First Traversal (DFS)
In DFS, we print a vertex and then recursively call DFS for its adjacent vertices. In topological sorting, we need to print a vertex before its adjacent vertices. For example, in the given graph, the vertex ‘5’ should be printed before vertex ‘0’, but unlike DFS, the vertex ‘4’ should also be printed before vertex ‘0’. So Topological sorting is different from DFS. For example, a DFS of the shown graph is “5 2 3 1 0 4”, but it is not a topological sorting.
Algorithm to find Topological Sorting
We recommend to first see the implementation of DFS. We can modify DFS to find Topological Sorting of a graph. In DFS, we start from a vertex, we first print it and then recursively call DFS for its adjacent vertices. In topological sorting, we use a temporary stack. We don’t print the vertex immediately, we first recursively call topological sorting for all its adjacent vertices, then push it to a stack. Finally, print contents of the stack. Note that a vertex is pushed to stack only when all of its adjacent vertices (and their adjacent vertices and so on) are already in the stack.
Below image is an illustration of the above approach:
Following are the implementations of topological sorting. Please see the code for Depth First Traversal for a disconnected Graph and note the differences between the second code given there and the below code.
- C++


- Java


- Python


- C#


Output
Following is a Topological Sort of the given graph
5 4 2 3 1 0
Complexity Analysis
- Time Complexity: O(V+E).
The above algorithm is simply DFS with an extra stack. So time complexity is the same as DFS which is. - Auxiliary space: O(V).
The extra space is needed for the stack.
Note: Here, we can also use vector instead of the stack. If the vector is used then print the elements in reverse order to get the topological sorting.
|
81 videos|113 docs|33 tests
|





















