Transformation of Stress & Strain - 2 | Solid Mechanics - Mechanical Engineering PDF Download

Theories of Failures

When a structural element is subjected to a system of complex stress system, it is important to predict the mode of failure so that the design methodology may be based on a particular failure criterion.
Theories of failure are essentially a set of failure criteria developed for the ease of design.
In structural design of an element is said to have failed if it ceases to perform its function.

There are basically two types of mechanical failure

• Yielding: This is due to excessive inelastic deformation rendering the machine part unsuitable to perform its function. This mostly occurs in ductile materials.
• Fracture: In this case the component tears apart in two or more parts. This mostly occurs in brittle materials.

Failure: In order to design the cotter joint and find out the dimensions, failure, in different parts and different cross-sections are considered.

There are many instances when a ductile material may fail by fracture. This may occur if a material is subjected to

• Cyclic loading
• Long term static loading at elevated temperature
• Impact loading
• Work hardening
• Severe quenching

Factor of safety (F.O.S): The ratio of ultimate to allowable load or stress is known as factor of safety i.e. The factor of safety can be defined as the ratio of the material strength or failure stress to the allowable or working stress.
The factor of safety must be always greater than unity. It is easier to refer to the ratio of stresses since this applies to material properties.
F.O.S = failure stress / working or allowable stress;

Ductile and Brittle Materials

• A ductile material deforms significantly before fracturing.
• Ductility is measured by % elongation at the fracture point.
• Materials with 5% or more elongation are considered ductile
• The limiting strength of ductile materials is the stress at yield point.
• A brittle material yields very little before fracturing, the yield strength is approximately the same as the ultimate strength in tension.
• The ultimate strength in compression is much larger than the ultimate strength in tension.
• The limiting strength of brittle materials is the ultimate stress

Static Failure Theories: Predicting failure in members subjected to uni-axial stress is both simple and straight-forward. But, predicating the failure stresses for members subjected to bi-axial or tri-axial stresses is much more complicated. A large numbers of different theories have been formulated. The principal theories of failure for a member subjected to biaxial stress are as follows:

• Maximum Principal / Normal Stress Theory (Rankine’s Theory)
• Maximum Shear Stress Theory (Tresca Theory)
• Maximum Principal / Normal Strain Theory (Saint’s Theory)
• Maximum Strain Energy Theory (Haigh’s Theory)
• Maximum Distortion Energy Theory (Hencky & Von Mises Theory)

1. Maximum Principal Stress Theory (Rankine Theory)
   (i) If one of the principal stresses σ1 (maximum principal stress), σ2 (minimum principal stress) or σ3 exceeds the yield stress, yielding would occur.
   (ii) In a two dimensional loading situation for a ductile material where tensile and compressive yield stress are nearly of same magnitude.
   σ₁ = ±σy
   σ₂ = ±σy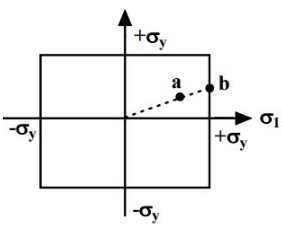
   (iii) Yielding occurs when the state of stress is at the boundary of the rectangle.
   (iv) At a point a, the stresses are still within the elastic limit but at b, σ1 reaches σy although σ2 is still less than σy.
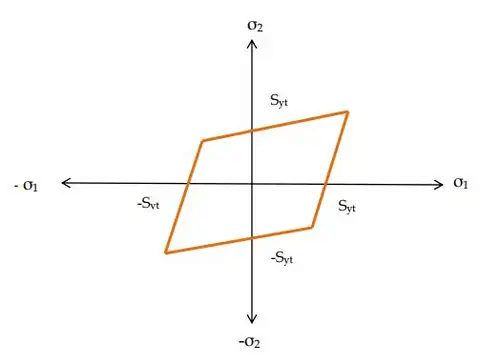
   (v) Yielding will then begin at point b.
2. Maximum Principal Strain Theory (St. Venant’s theory)
   (i) Yielding will occur when the maximum principal strain just exceeds the strain at the tensile yield point in either simple tension or compression. If ε1 and ε2 are maximum and minimum principal strains corresponding to σ1 and σ2, in the limiting case:
   ε₁ = 1 / E(σ₁ - vσ₂)|σ₁| ≥ |σ₂|
   ε₂ = 1 / E(σ₂ - vσ₁)|σ₂| ≥ |σ₁|
   It implies:
   Eε₁ = σ₁ - vσ₂ = ±σ₀
   Eε_2 = σ_2 - vσ₁ = ±σ₀
   (ii) Boundary of a yield surface in Maximum Strain Energy Theory is given below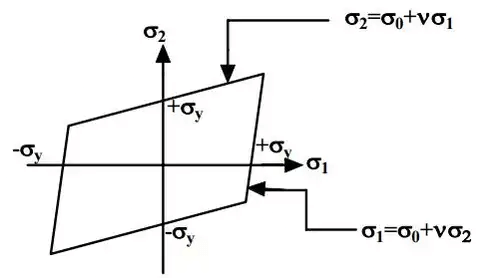
   
3. Maximum Shear Stress Theory (Tresca Theory)
   (i) Yielding would occur when the maximum shear stress just exceeds the shear stress at the tensile yield point. At the tensile yield point σ2 = σ3 = 0 and thus maximum shear stress is σy / 2.
   This gives us six conditions for a three-dimensional stress situation:
   σ₁ - σ₂ = ±σ_y
   σ₂ - σ₃ = ±σ_y
   σ₃ - σ₁= ±σ_y
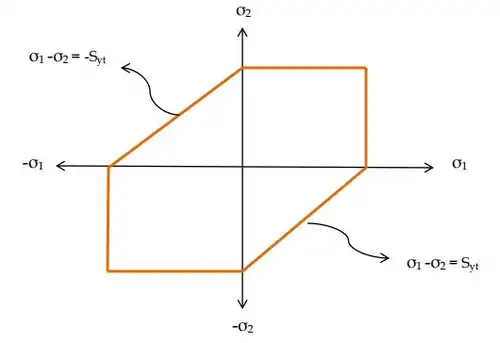
   (ii) Yield surface corresponding to maximum shear stress theory in biaxial stress situation is given below :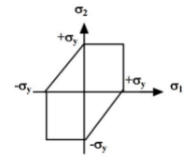
   
4. Maximum strain energy theory ( Beltrami’s theory)
   (i) Failure would occur when the total strain energy absorbed at a point per unit volume exceeds the strain energy absorbed per unit volume at the tensile yield point. This may be given
   1 / 2(σ₁ε₁ + σ₂ε₂ + σ₃ε₃) = 1 / 2σ_yε_y
   Substituting, ε₁, ε₂ , ε₃ and εy in terms of stresses we have
   σ₁² + σ₂² + σ₃² - 2ν (σ₁σ₂ + σ₂σ₃ + σ₃σ₁) = σ_y²
   (σ₁ / σ_y)² + (σ₂ + σ_y)²  - 2v(σ₁σ² / σ_y²) = 1
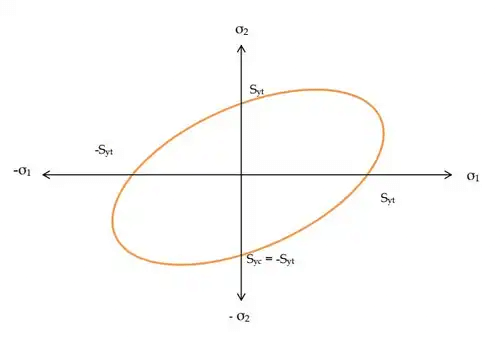
   (ii) Above equation results in Elliptical yield surface which can be viewed as: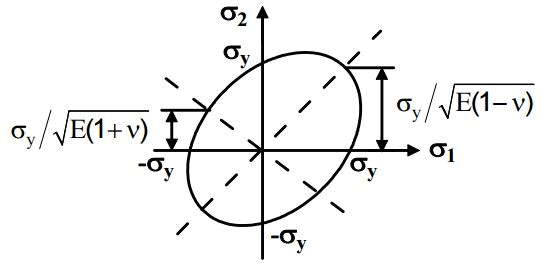
   
5. Distortion energy theory (Von Mises yield criterion)
   (i) Yielding would occur when total distortion energy absorbed per unit volume due to applied loads exceeds the distortion energy absorbed per unit volume at the tensile yield point. Total strain energy E_T and strain energy for volume change E_V can be given as:
   ET = 1/2(σ₁ε₁ + σ₂ε₂ + σ₃ε₃) and E_V = 3/2σ_avε_av
   Substituting strains in terms of stresses the distortion energy can be given as:
   E_d = E_T - E_V = 2(1 + V)6E(σ₁² + σ₂² + σ₃² - σ₁σ₂ - σ₂σ₃ - σ₃σ₁)
   At the tensile yield point, σ1 = σy , σ2 = σ3 = 0 which gives,
   E_dy = (2(1 + v) / 6E)σ²_y
   The failure criterion is thus obtained by equating Ed and Edy, which gives
    (σ₁ - σ₂)²+(σ₂ - σ₃)²+(σ₃ - σ₁)² = 2σ²_y
   In a 2-D situation if σ3 = 0, so the equation reduces to,
   (σ₁ / σ_y)² + (σ₂ / σ_y)² - (σ₁ / σ_y)(σ₂ / σ_y) = 1
   (ii) This is an equation of ellipse and yield equation is an ellipse.
   (iii) This theory is widely accepted for ductile materials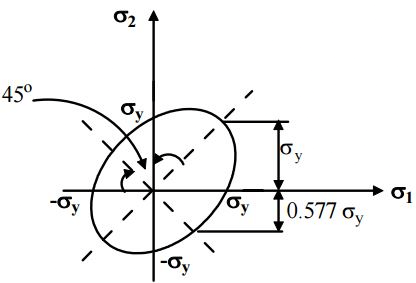
    

Shape of safe boundaries for theories of failure 

Graphical representation or safe boundaries are used to check whether the given dimensions of a component are safe or not under given loading conditions.
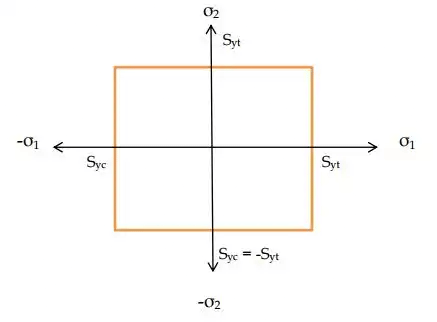
As per theories of failure for ductile material, Ultimate tensile strength (S_ut) = Yield strength (S_yt)

1. Maximum Principal Stress Theory: Square
    
2. Maximum Shear Stress Theory: Hexagon
   
3. Maximum Principal Strain Theory: Rhombus
4. Total Strain Energy Theory: Ellipse
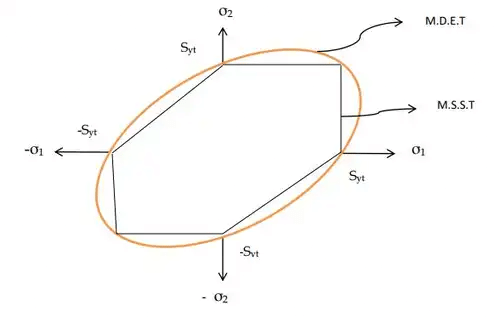
5. Maximum Distortion Energy Theory: Ellipse
   

Note:

• All the theories of the failure will give the same result when uniaxial state of stress. Examples:
  (a) Bar subjected to uniaxial load.
  (b) Beam subjected to pure bending.
• All the theories of the failure will give the same result when one of the principal stresses is very large as compared to the other principal stresses.
• For pure shear state of stress, all the theories of failure will give the different result.
  (a) MDET and MSST will be used under pure shear state of stress.
  (b) MDET will be preferred over MSST.
• MSST and MDET are not valid for the hydrostatic state of stress condition.
• TSET and MPST will be used for the hydrostatic state of stress condition. TSET will be preferred over MPST.