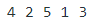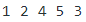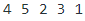Tree Transversal | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
Introduction
Unlike linear data structures (Array, Linked List, Queues, Stacks, etc) which have only one logical way to traverse them, trees can be traversed in different ways. The following are the generally used methods for traversing trees:
Example
Inorder Traversal (Practice)
Algorithm Inorder(tree)
- Traverse the left subtree, i.e., call Inorder(left->subtree)
- Visit the root.
- Traverse the right subtree, i.e., call Inorder(right->subtree)
Uses of Inorder Traversal
In the case of binary search trees (BST), Inorder traversal gives nodes in non-decreasing order. To get nodes of BST in non-increasing order, a variation of Inorder traversal where Inorder traversal is reversed can be used.
Example: In order traversal for the above-given figure is 4 2 5 1 3.
// C program for different tree traversals
#include <stdio.h>
#include <stdlib.h>
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct node {
int data;
struct node* left;
struct node* right;
};
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newNode(int data)
{
struct node* node
= (struct node*)malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
/* Given a binary tree, print its nodes in inorder*/
void printInorder(struct node* node)
{
if (node == NULL)
return;
/* first recur on left child */
printInorder(node->left);
/* then print the data of node */
printf("%d ", node->data);
/* now recur on right child */
printInorder(node->right);
}
/* Driver code*/
int main()
{
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
// Function call
printf("\nInorder traversal of binary tree is \n");
printInorder(root);
getchar();
return 0;
}
Output
Inorder traversal of binary tree is
Time Complexity: O(N)
Auxiliary Space: If we don’t consider the size of the stack for function calls then O(1) otherwise O(h) where h is the height of the tree.
Preorder Traversal (Practice)
Algorithm Preorder(tree)
- Visit the root.
- Traverse the left subtree, i.e., call Preorder(left->subtree)
- Traverse the right subtree, i.e., call Preorder(right->subtree)
Uses of Preorder
Preorder traversal is used to create a copy of the tree. Preorder traversal is also used to get prefix expressions on an expression tree.
Example: Preorder traversal for the above-given figure is 1 2 4 5 3.
// C program for different tree traversals
#include <stdio.h>
#include <stdlib.h>
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct node {
int data;
struct node* left;
struct node* right;
};
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newNode(int data)
{
struct node* node
= (struct node*)malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
/* Given a binary tree, print its nodes in preorder*/
void printPreorder(struct node* node)
{
if (node == NULL)
return;
/* first print data of node */
printf("%d ", node->data);
/* then recur on left subtree */
printPreorder(node->left);
/* now recur on right subtree */
printPreorder(node->right);
}
/* Driver code*/
int main()
{
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
// Function call
printf("\nPreorder traversal of binary tree is \n");
printPreorder(root);
getchar();
return 0;
}
Output
Preorder traversal of binary tree is
Time Complexity: O(N)
Auxiliary Space: If we don’t consider the size of the stack for function calls then O(1) otherwise O(h) where h is the height of the tree.
Postorder Traversal (Practice)
Algorithm Postorder(tree)
- Traverse the left subtree, i.e., call Postorder(left->subtree)
- Traverse the right subtree, i.e., call Postorder(right->subtree)
- Visit the root
Uses of Postorder
Postorder traversal is used to delete the tree. Please see the question for the deletion of a tree for details. Postorder traversal is also useful to get the postfix expression of an expression tree
Example: Postorder traversal for the above-given figure is 4 5 2 3 1
Below is the implementation of the above traversal methods:
// C program for different tree traversals
#include <stdio.h>
#include <stdlib.h>
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct node {
int data;
struct node* left;
struct node* right;
};
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newNode(int data)
{
struct node* node
= (struct node*)malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
/* Given a binary tree, print its nodes according to the
"bottom-up" postorder traversal. */
void printPostorder(struct node* node)
{
if (node == NULL)
return;
// first recur on left subtree
printPostorder(node->left);
// then recur on right subtree
printPostorder(node->right);
// now deal with the node
printf("%d ", node->data);
}
/* Driver code*/
int main()
{
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
// Function call
printf("\nPostorder traversal of binary tree is \n");
printPostorder(root);
getchar();
return 0;
}
Output
Postorder traversal of binary tree is
Time Complexity: O(N)
Auxiliary Space: If we don’t consider the size of the stack for function calls then O(1) otherwise O(h) where h is the height of the tree.
Note: The height of the skewed tree is n (no. of elements) so the worst space complexity is O(N) and the height is (Log N) for the balanced tree so the best space complexity is O(Log N).
Let us see different corner cases
Complexity function T(n) — for all problems where tree traversal is involved — can be defined as: T(n) = T(k) + T(n – k – 1) + c
Where k is the number of nodes on one side of the root and n-k-1 on the other side.
Let’s do an analysis of boundary conditions:
Case 1: Skewed tree (One of the subtrees is empty and another subtree is non-empty )
k is 0 in this case.
T(n) = T(0) + T(n-1) + c
T(n) = 2T(0) + T(n-2) + 2c
T(n) = 3T(0) + T(n-3) + 3c
T(n) = 4T(0) + T(n-4) + 4c
…………………………………………
………………………………………….
T(n) = (n-1)T(0) + T(1) + (n-1)c
T(n) = nT(0) + (n)c
Value of T(0) will be some constant say d. (traversing an empty tree will take some constants time)
T(n) = n(c+d)
T(n) = Θ(n) (Theta of n)
Case 2: Both left and right subtrees have an equal number of nodes.
T(n) = 2T(|_n/2_|) + c
This recursive function is in the standard form (T(n) = aT(n/b) + (-)(n) ) for master method. If we solve it by master method we get (-)(n)
|
158 docs|30 tests
|