Addition & Subtraction of Vectors (Triangular & Parallelogram Laws) - Graphical Method | Physics for JAMB PDF Download
Addition of Vectors ( Graphical Method)
- Vectors can only be added if they are of the same type.
- For instance, a displacement vector cannot be combined with a force vector, but it can be added to another displacement vector.
- The graphical method for adding vectors helps visualize both the individual vectors and their resultant.
- This method uses specific laws to guide the process of vector addition:
1. Triangle Law of Vector Addition
2. Parallelogram Law of Vector Addition
3. Polygon Law of Vector Addition
1. Triangle Law of Vector Addition
If two vectors are acting on a body at the same time and are represented in both magnitude and direction by two sides of a triangle in sequence, then their resultant vector (in terms of both magnitude and direction) is represented by the third side of the triangle taken in the reverse order.
This method is specifically applicable for vector addition.
Steps for adding two vector representing same physical quantity by triangle law:
- Position the vectors so that the tail of one vector coincides with the head of the other.
- Join tail of first to head of the other by a line with arrow at head of the second.
- This new vector is the sum of two vectors. (also called resultant)
(i) (ii)
(iii)
Q1. A boy travels 10 m due to North and then 7m due to East. Find the displacement and direction of body.
Sol: Let the boy start moving from point O as shown in the figure.
where, OA = 10 m, due North
AB = 7 m, due East
 According to triangle law of vector addition, OB is the resultant displacement.
According to triangle law of vector addition, OB is the resultant displacement.
The magnitude of the resultant displacement,

Since, the resultant displacement makes an angle θ with the North direction. Then,
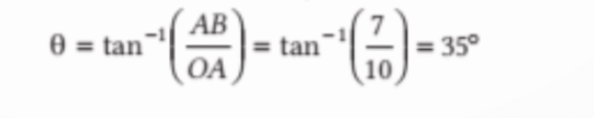
2. Parallelogram Law of Vector Addition
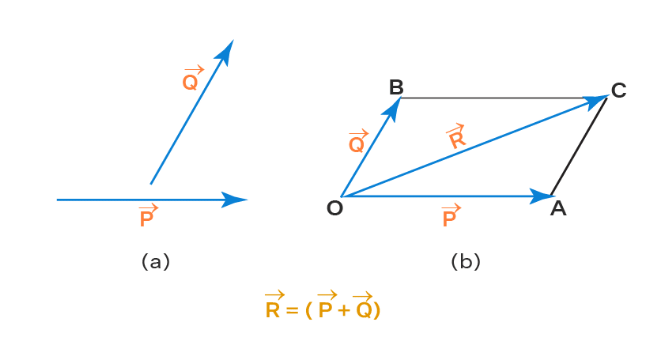
This law states that if two vectors are positioned as adjacent sides of a parallelogram with their tails connected, the sum of these two vectors will be represented by the diagonal of the parallelogram, starting from the same point as the two vectors.
Consider the vectors P and Q in the figure below. To find their sum:
- Draw the vectors P and Q such that their tails touch each other.
- Complete the parallelogram by drawing the other two sides.
- The diagonal of the parallelogram that has the same tail as the vectors P and Q represents the sum of the two vectors i.e., P + Q = R.
Note: Angle between 2 vectors is the angle between their positive directions.
Suppose angle between these two vectors is θ, and

(AD)2 = (AE)2 +(DE)2
= (AB + BE)2 + (DE)2
= (a +b cosθ)2 + (b sinθ)2
= a2 + b2 cos2θ + 2ab cosθ + b2 sin2θ
= a2 + b2 + 2ab cosθ
Thus, AD =
or
Angle α with vector a is
tan α = =
Important points :
- Only vectors of the same type, representing the same physical quantity, can be added together, and the resultant will also be a vector of the same type.
- As R = [A2 + B2 + 2AB cosθ]1/2 so R will be maximum when, cosθ = 1 (i.e., θ = 0º) i.e. vectors are like or parallel, yielding Rmax = A + B.
-
and angle between them θ then R =
-
and angle between them π -θ then R =
- The resultant will be minimum if, cosθ = -1 (i.e., θ = 180º), i.e. vectors are antiparallel, indicating Rmin = A -B.
- If the vectors A and B are orthogonal, i.e., θ = 90º,
- Minimum number of unequal coplanar vectors whose sum can be zero is three.
- The resultant of three non-coplanar vectors can never be zero, or minimum number of non coplanar vectors whose sum can be zero is four.
Q2. A body is simultaneously given two velocities of 30 m/s due East and 40 m/s due North, respectively. Find the resultant velocity.
Sol: Let the body be starting from point O as shown.

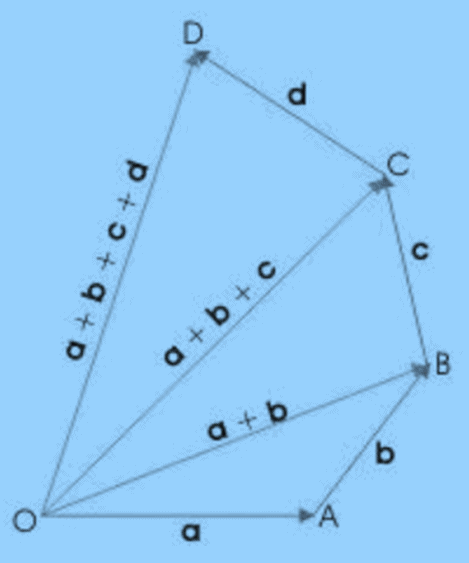
3. Polygon Law of Vector Addition
This law is used for adding more than two vectors. This is extension of triangle law of addition. We keep on arranging vectors such that tail of next vector lies on head of former.
When we connect the tail of first vector to head of last we get resultant of all the vectors.
Properties of Addition of Vectors:
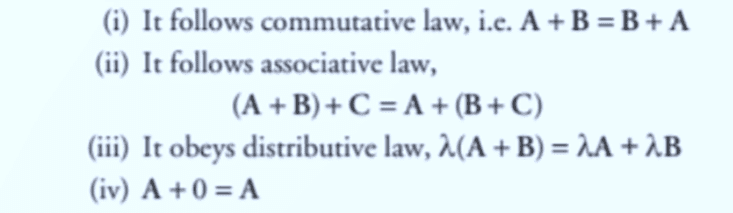
Subtraction of Vectors (Graphical Method)
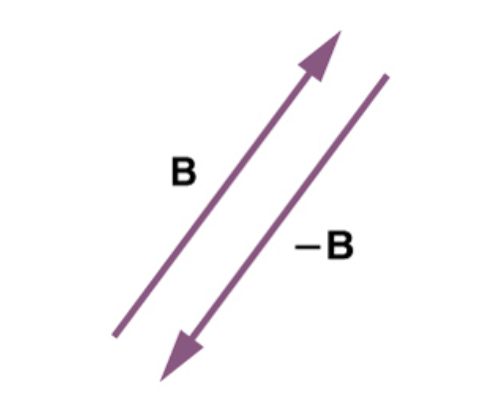
- Negative of a vector say
is a vector of the same magnitude as vector but pointing in a direction opposite to that of
.
- Thus,
can be expressed as
or
is the vector addition of
and
.
- Suppose angle between two vectors is θ. Then angle between
 and
and will be 180° -θ as shown in figure.
- Magnitude of
will be thus given by
- S =
=
- or S =
...(i)
- For direction of
we will either calculate angle α or β, where,
- tanα =
=
...(ii)
- or tanβ =
=
...(iii)
Properties of Subtraction of Vectors:

Q3. Two vectors of 10 units & 5 units make an angle of 120° with each other. Find the magnitude & angle of resultant with vector of 10 unit magnitude.
Sol: =
⇒ α = 30°
[Here shows what is angle between both vectors = 120° and not 60°]
Note: or can also be found by making triangles as shown in the figure. (a) and (b)
Or
Q4. Two vectors of equal magnitude 2 are at an angle of 60° to each other. Find the magnitude of their sum & difference.
Sol:
Q5. Find and
in the diagram shown in figure. Given A = 4 units and B = 3 units.
Sol: Addition :
R =
= =
units
tanα = =
= 0.472
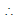 a = tan-1(0.472) = 25.3°
a = tan-1(0.472) = 25.3°
Thus, resultant of and
is
units at angle 25.3° from
in the direction shown in figure.
Subtraction : S =
= =
and tanθ =
= = 1.04
∴ α = tan-1 (1.04) = 46.1°
Thus, is
units at 46.1° from
in the direction shown in figure.
|
259 videos|253 docs|230 tests
|
FAQs on Addition & Subtraction of Vectors (Triangular & Parallelogram Laws) - Graphical Method - Physics for JAMB
| 1. What is the Triangle Law of Vector Addition? |  |
| 2. How does the Parallelogram Law of Vector Addition work? |  |
| 3. What is the Polygon Law of Vector Addition? |  |
| 4. How can vectors be subtracted graphically? |  |
| 5. What are the applications of vector addition and subtraction in real life? |  |

















