Trigonometry - Examples (with Solutions), Geometry, Quantitative Aptitude CAT Notes | EduRev
Quantitative Aptitude for GMAT
GMAT : Trigonometry - Examples (with Solutions), Geometry, Quantitative Aptitude CAT Notes | EduRev
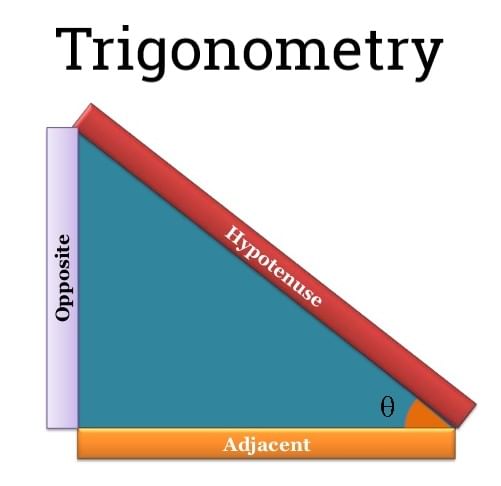
Angles and their relationship
Angles are measured in many units’ viz. degrees, minutes, seconds, radians, gradients.
Where 1 degree = 60 minutes, 1 minute = 60 seconds,
π radians = 180° = 200g
⇒ 1 radian = 180°/π and 1 degree = π/ 180 radians.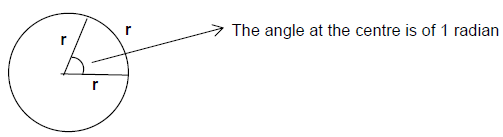
Basic Trigonometric Ratios
In a right triangle ABC, if θ be the angle between AC & BC.
If θ is one of the angle other then right angle, then the side opposite to the angle is perpendicular (P) and the
sides containing the angle are taken as Base ( B) and the hypotenuse (H). In this type of triangles, we can
have six types of ratios. These ratios are called trigonometric ratios.
Important Formulae
Range of Values of Ratios
If 0 ≤ θ ≤ 360o, then the values for different trigonometric ratios will be as follows.
1. - 1 ≤ Sin θ ≤ 1
2. - 1 ≤ cos θ ≤ 1
3. - ∞ ≤ tan θ ≤ ∞
4. - ∞ ≤ cot θ ≤ ∞
5. - ∞ ≤ Sec θ ≤ -1 & 1 ≤ Sec θ ≤ ∞
6. - ∞ ≤ Cosec θ ≤ - 1 & 1 ≤ Cosec θ ≤ ∞
Sign of Trigonometric ratios
We divide the angle at a point (i.e. 360°) into 4 parts called quadrants. In the first quadrant all the
trigonometric ratios are positive
SOME MORE RESULTS:
Ex.1 Simplify .
Sol.
Ex.2 If cot A 
, find the value of 3 cos A + 4 sin A, where A is in the first quadrant.
Sol.
Ex.3 Find the value of
Sol.
= 1 + 1 - 1 = 1
Values of trigonometric Ratio for some special angles:
Properties of triangle
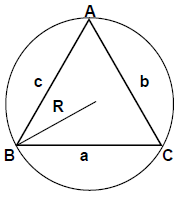
Sine Rule
In any triangle ABC if AB, BC, AC be represented by c, a, b respectively
Cosine Rule
In a triangle ABC of having sides of any size, we have the following rule;
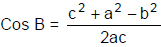
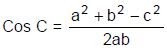
Area of triangle
Up next >
Introduction to Basic Trigonometry, Quantitative Aptitude
- Video | 08:45 min
Test: Heights And Distances - 1
- Test | 10 ques | 20 min
Introduction to Trigonometry : 2, Quantitative Aptitude
- Video | 05:56 min
< Previous
- Test: Trigonometry- 2
- Test | 10 ques | 20 min
- Test: Trigonometry- 1
- Test | 10 ques | 20 min
- Basic Trigonometry Concepts
- Doc | 3 pages
- Short Review of Trigonometry
- Doc | 5 pages
Dynamic Test
Content Category
Related Searches
mock tests for examination
,Geometry
,Geometry
,Previous Year Questions with Solutions
,Quantitative Aptitude CAT Notes | EduRev
,MCQs
,Semester Notes
,Summary
,Extra Questions
,past year papers
,Sample Paper
,Trigonometry - Examples (with Solutions)
,Objective type Questions
,Quantitative Aptitude CAT Notes | EduRev
,Quantitative Aptitude CAT Notes | EduRev
,Viva Questions
,Exam
,video lectures
,Free
,Geometry
,Important questions
,ppt
,shortcuts and tricks
,study material
,practice quizzes
,Trigonometry - Examples (with Solutions)
,Trigonometry - Examples (with Solutions)
;
