Types of Fractions | Mathematics for Digital SAT PDF Download

Fractions

• Fractions are an essential part of mathematics, used to represent the parts of a whole object. A fraction comprises of two terms: the numerator and the denominator. There are three primary types of fractions based on the numerator and denominator: proper fractions, improper fractions, and mixed fractions.
• Apart from these three types, there are three more types of fractions based on their comparison with other fractions, namely like fractions, unlike fractions, and equivalent fractions. In total, there are six types of fractions.
• Proper fractions have a numerator that is smaller than the denominator, while improper fractions have a numerator greater than the denominator. Mixed fractions are a combination of a natural number and a fraction. Like fractions have the same denominator, whereas unlike fractions have different denominators. Equivalent fractions have the same value but can have different numerators and denominators.

In real-life scenarios, we often encounter measured quantities that are not whole numbers, and fractions help us deal with parts and portions of whole things.

Proper Fraction

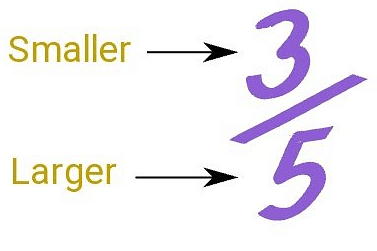
For Example: 1/3, 2/5, and 3/8 are all proper fractions because the numerator is less than the denominator. In these fractions, the value of the fraction is less than 1, which means that the fraction represents a part of a whole object or a quantity that is smaller than the whole.

Since the numerator of a proper fraction is less than the denominator, the value of the fraction is always less than 1. 

Improper Fraction

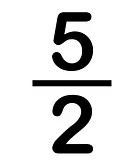i.e., Numerator > Denominator

For Example: An example of an improper fraction is 17/5, where the numerator (17) is greater than the denominator (5).

Remember:

• All the natural numbers can be represented in the form of fractions, where the denominator is always equal to 1.
• The simplification of improper fraction results in the value which is equal or greater than 1, but not less than 1.

Mixed Fraction

Remember:

• Mixed fractions can always be converted into a fraction.
• An improper fraction can be converted into a mixed fraction.
• A mixed fraction is always greater than 1.

Like Fractions

The simplification of such fractions is easy, as all the denominators here are the same. Suppose we need to add all the above like fractions, then;
1/2 + 3/2 + 5/2 + 7/2 = (1+3+5+7)/2 = 16/2 = 8

Unlike Fractions

Simplication for such fractions is a little lengthy method since we need to factorise the denominator first and then simplify them (in case of addition and subtraction).
Suppose, we have to add 1/2 and 1/3. Then first we will find the LCM of 2 and 3 which is equal to 6.
Now we need to multiply 1/2 by 3 and 1/3 by 2, both in numerator and denominator.
The fractions become 3/6 and 2/6.
Now if we add 3/6 and 2/6, we get;
3/6+2/6 = 5/6

Equivalent Fractions

1/2 and 2/4 are equivalent.
1/3 and 3/9 are equivalent.