Types of Matrices | Business Mathematics and Statistics - B Com PDF Download
What are Types of Matrices?
This article describes some of the important types of matrices that are used in mathematics, engineering, and science. Here is the list of the most commonly used types of matrices in linear algebra:
- Row Matrix & Column Matrix
- Rectangular Matrix & Square Matrix
- Identity Matrix
- Zero Matrix
- Diagonal Matrix
- Singular Matrix & Nonsingular Matrix
- Hermitian Matrix & Skew-Hermitian Matrix
- Upper & Lower Triangular Matrices
- Symmetric Matrix and Skew Symmetric Matrix
- Orthogonal Matrix
We can use these different types of matrices to organize data by age group, person, company, month, and so on. We can then use this information to make decisions and solve a lot of math problems.
Identifying Types of Matrices
Matrices are in all sorts of sizes, but usually, their shapes remain the same. The size of a matrix is called its order which is the total number of rows and columns in a given matrix. In the below-given image, we can see how the dimension of a matrix is calculated. In this section, let's learn to identify the types of matrices based on their dimension:
In this section, let's learn to identify the types of matrices based on their dimension:
Row and Column Matrix
Matrices with only one row and any number of columns are known as row matrices and matrices with one column and any number of rows are called column matrices. Let's look at two examples below:
Rectangular and Square Matrix
Any matrix that does not have an equal number of rows and columns is called a rectangular matrix and a rectangular matrix can be denoted by Bm × n. Any matrix that has an equal number of rows and columns is called a square matrix and a square matrix can be denoted by Bn × n. Let's look at the examples below:

Identity and Zero Matrices
Let's look at the identity matrix and zero matrix.
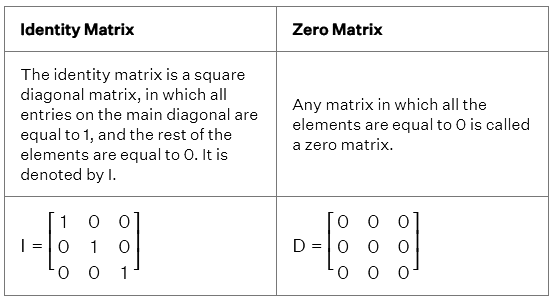
Other Types of Matrices
Apart from the most commonly used matrices, there are other types of matrices that are used in advanced mathematics and computer technologies. Following are some of the other types of matrices:
Singular and Non-singular Matrix
Any square matrix whose determinant is equal to 0 is called a singular matrix and any matrix whose determinant is not equal to 0 is called a non-singular matrix. The determinant of a matrix can be found by using determinant formula. Let's look at two examples below:

Diagonal Matrix
A square matrix in which all the elements are 0 except for those elements that are in the diagonal is called a diagonal matrix. Let's take a look at the examples of different kinds of diagonal matrices: A scalar matrix is a special type of square diagonal matrix, where all the diagonal elements are equal.

Upper and Lower Triangular Matrix
An upper triangular matrix is a square matrix where all the elements that are present below the diagonal elements are 0. A lower triangular matrix is a square matrix where all the elements that are present above the diagonal elements are 0. Let's look at the examples below:

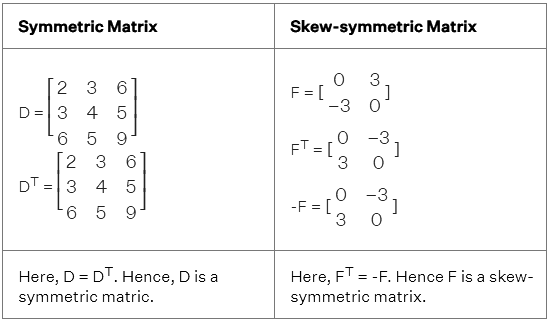
Symmetric and Skew Symmetric Matrix
A square matrix D of size n×n is considered to be symmetric if and only if DT= D. A square matrix F of size n×n is considered to be skew-symmetric if and only if FT= - F. Let's consider the examples of two matrices D and F:
Hermitian and Skew Hermitian Matrices
There is a small difference between the symmetric and hermitian matrices.
- A matrix is said to be hermitian if and only it is equal to the transpose of its conjugate matrix.
Example:
- A matrix is said to be skew hermitian if and only if it is equal to the negative of its conjugate matrix.
Example:
Boolean Matrix
A matrix is considered to be a boolean matrix when all its elements are either 1s and 0s. Let's consider the example of the matrix B to understand this better:
Stochastic Matrices
A stochastic matrix is a type of matrix whose all entries represent probability. A square matrix C is considered to be left stochastic when all of its entries are non-negative and when the entries in each column sum to 1. Similarly, a matrix with all its entries as non-negative such that entries in each row sum to 1 is called a right stochastic matrix. Consider the example of a left stochastic matrix C here:
Orthogonal Matrix
A square matrix B is considered to be an orthogonal matrix, when B × BT = I, where I is an identity matrix and BT is the transpose of matrix B. Take an example of the matrix B: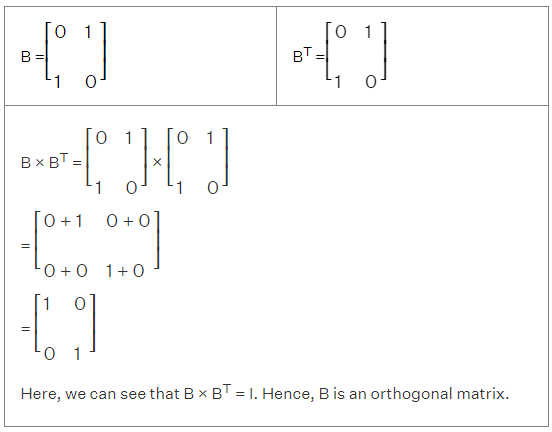
Special Matrices
Apart from what we have learned so far, there are some special types of matrices:
Idempotent Matrix
A square matrix A is said to be an idempotent matrix if and only if An = A, for every n ≥ 2. For example, A2 = A, A3 = A, and so on. To check whether a square matrix A is idempotent, it is sufficient to check whether A2 = A.
Nilpotent Matrix
A square matrix A of order n is nilpotent if and only if Ak = O for some k ≤ n. For example, A =
 is a nilpotent matrix as A2 = O, where O is null matrix of order 2.
is a nilpotent matrix as A2 = O, where O is null matrix of order 2.Involutory Matrix
A square matrix A is called an involutory matrix if and only A-1 = A. For example, an identity matrix is involutory as it is equal to its inverse.
Important Notes on Types of Matrices:
- Matrices with only one row and any number of columns are known as row matrices.
- Matrices with one column and any number of rows are called column matrices.
- Constant matrices are matrices in which all the elements are constants for any given dimension/order of the matrix.
|
115 videos|142 docs
|
FAQs on Types of Matrices - Business Mathematics and Statistics - B Com
| 1. What are the different types of matrices based on their dimensions? |  |
| 2. How can matrices be categorized based on their properties? |  |
| 3. What is the difference between a square matrix and a rectangular matrix? |  |
| 4. What are the characteristics of an identity matrix? |  |
| 5. How can a matrix be classified as diagonal, upper triangular, and lower triangular? |  |

|
Explore Courses for B Com exam
|

|




















