Types of Numbers | Quantitative Reasoning for GRE PDF Download
An arithmetic value that is expressed using a word, a symbol or a figure that represents a quantity is called a number. Numbers are used in counting and calculations.
Types of Numbers
The different types of numbers depend on the properties that they have. For example, natural numbers are counting numbers that start from 1, whereas, whole numbers start from 0, prime numbers are only divisible by 1 and the number itself, and so on. Let us learn more about the different types of numbers in the following sections.
1. Natural Numbers
The group of numbers starting from 1 and including 1, 2, 3, 4, 5, and so on. Zero, negative numbers, and decimals are not included in this group.2. Whole Numbers
All Natural Numbers plus the number 0 are called as Whole Numbers.
3. Integers
All Whole Numbers and their negatives are included in this group.The integers are represented by the symbol ‘Z’.
Z= {……-8,-7,-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8,……}
Integers come in three types:
~ Zero (0)
~ Positive Integers (Natural numbers)
~ Negative Integers (Additive inverse of Natural Number)
4. Rational Numbers
Any number that can be expressed as a ratio of two integers is called a rational number.
This group contains decimal that either do not exist (as in 6 which is 6/1), or terminate (as in 3.4 which is 34/10), or repeat with a pattern (as in 2.333... which is 7/3).
5. Irrational Numbers
- Any number that can not be expressed as the ratio of two integers is called an irrational number (imaginary or complex numbers are not included in irrational numbers).
- These numbers have decimals that never terminate and never repeat with a pattern.
- The common examples of irrational numbers are pi(π=3⋅14159265…), √2, √3, √5, Euler’s number (e = 2⋅718281…..), 2.010010001….,etc.
6. Real Numbers
This group is made up of all the Rational and Irrational Numbers. The ordinary number line encountered when studying algebra holds real numbers.
7. Imaginary Numbers
An imaginary number is one of the form bi where b is a real number and i is the imaginary element derived from i2 = (-1). Imaginary numbers were defined to enable the solutions of equations requiring the square roots of negative number
8. Complex Numbers
A Complex Number is a combination of a real number and an imaginary number in the form a + bi. a is called the real part and b is called the imaginary part.
Examples include 3 + 6i
Note:
A number in the formis written in the form of a complex number by a+lb multiplying both numerator and denominator by the conjugate of a + ib, i.e. a - ib. Hence,
which is in the form p + iq
9. Prime Numbers
All the numbers that have only two divisors, 1 and the number itself, are called prime numbers. Hence, a prime number can only be written as the product of 1 and itself. The numbers 2, 3, 5, 7, 11, 37, etc. are prime numbers.
Note:
1 is not a prime number.
Example:
Ques 1: If x2 - y2 = 101, find the value of x2 + y2, given that x and y are natural numbers.
Ans: x2 - y2 = (x + y)(x - y) = 101. But 101 is a prime number and cannot be written as product of two numbers unless one of the numbers is 1 and the other is 101 itself.
Hence, x + y = 101 and x - y = 1. -> x = 51, y = 50.
-> x2 + y2 = 512 + 502 = 5101.
Ques 2: What numbers have exactly three divisors?
Ans: The squares of prime numbers have exactly three divisors, i.e. 1, the prime number, and the square itself.
To find whether a number N is prime or not
Find the root R (approximate) of the number N, i.e. R = √N. Divide N by every prime number less than or equal to R. If N is divisible by at least one of those prime numbers it is not a prime number. If N is not divisible by any of those prime numbers, it is a prime number.
10. Odd and Even Numbers
All the numbers divisible by 2 are called even numbers whereas all the numbers not divisible by 2 are called odd numbers. 2, 4, 6, 8 etc. are even numbers and 1, 3, 5, 7.. etc. are odd numbers.
Remember!
• Odd + Odd = Even
• Even + Even = Even
• Odd + Even = Odd
• (Odd)Even = Odd
• (Even)Odd = Even
• Even x Odd = Even
• Even x Even = Even
• Odd x Odd = Odd
• (Odd)Even x (Even)Odd = Even
• (Odd)Even + (Even)Odd = Odd
|
93 videos|77 docs|104 tests
|
FAQs on Types of Numbers - Quantitative Reasoning for GRE
| 1. What are natural numbers? |  |
| 2. What are whole numbers? |  |
| 3. What are integers? |  |
| 4. What are rational numbers? |  |
| 5. What are irrational numbers? |  |

|
Explore Courses for GRE exam
|

|
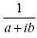 is written in the form of a complex number by a+lb multiplying both numerator and denominator by the conjugate of a + ib, i.e. a - ib. Hence,
is written in the form of a complex number by a+lb multiplying both numerator and denominator by the conjugate of a + ib, i.e. a - ib. Hence, which is in the form p + iq
which is in the form p + iq

















