Types of Relations | Algebra - Mathematics PDF Download
Relation
A connection between the elements of two or more sets is Relation. The sets must be non-empty. A subset of the Cartesian product also forms a relation R. A relation may be represented either by Roster method or by Set-builder method.
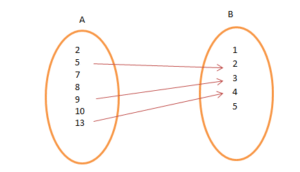
Let A and B be two sets such that A = {2, 5, 7, 8, 10, 13} and B = {1, 2, 3, 4, 5}. Then,
R = {(x, y): x = 4y – 3, x ∈ A and y ∈ B} (Set-builder form)
R = {(5, 2), (10, 3), (13, 4)} (Roster form)
Types of Relations or Relationship
Let us study about the various types of relations.
Empty Relation
If no element of set X is related or mapped to any element of X, then the relation R in A is an empty relation, i.e, R = Φ. Think of an example of set A consisting of only 100 hens in a poultry farm. Is there any possibility of finding a relation R of getting any elephant in the farm? No! R is a void or empty relation since there are only 100 hens and no elephant.
Universal Relation
A relation R in a set, say A is a universal relation if each element of A is related to every element of A, i.e., R = A × A. Also called Full relation. Suppose A is a set of all natural numbers and B is a set of all whole numbers. The relation between A and B is universal as every element of A is in set B. Empty relation and Universal relation are sometimes called trivial relation.
Identity Relation
In Identity relation, every element of set A is related to itself only. I = {(a, a), ∈ A}. For example, If we throw two dice, we get 36 possible outcomes, (1, 1), (1, 2), … , (6, 6). If we define a relation as R: {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}, it is an identity relation.
Inverse Relation
Let R be a relation from set A to set B i.e., R ∈ A × B. The relation R-1 is said to be an Inverse relation if R-1 from set B to A is denoted by R-1 = {(b, a): (a, b) ∈ R}. Considering the case of throwing of two dice if R = {(1, 2), (2, 3)}, R-1 = {(2, 1), (3, 2)}. Here, the domain of R is the range of R-1 and vice-versa.
Reflexive Relation
If every element of set A maps to itself, the relation is Reflexive Relation. For every a ∈ A, (a, a) ∈ R.
Symmetric Relation
A relation R on a set A is said to be symmetric if (a, b) ∈ R then (b, a) ∈ R, for all a & b ∈ A.
Transitive Relation
A relation in a set A is transitive if, (a, b) ∈ R, (b, c) ∈ R, then (a, c) ∈ R, for all a, b, c ∈ A
Equivalence Relation
A relation is said to be equivalence if and only if it is Reflexive, Symmetric, and Transitive. For example, if we throw two dices A & B and note down all the possible outcome.
Define a relation R= {(a, b): a ∈ A, b ∈ B}, we find that {(1, 1), (2, 2), …, (6, 6) ∈ R} (reflexive). If {(a, b) = (1, 2) ∈ R} then, {(b, a) = (2, 1) ∈ R} (symmetry). ). If {(a, b) = (1, 2) ∈ R} and {(b, c) = (2, 3) ∈ R} then {(a, c) = (1, 3) ∈ R} (transitive)
Solved Example for You
Problem: Three friends A, B, and C live near each other at a distance of 5 km from one another. We define a relation R between the distances of their houses. Is R an equivalence relation?
Solution: For an equivalence Relation, R must be reflexive, symmetric and transitive.
- R is not reflexive as A cannot be 5 km away to itself.
- The relation, R is symmetric as the distance between A & B is 5 km which is the same as the distance between B & A.
- R is transitive as the distance between A & B is 5 km, the distance between B & C is 5 km and the distance between A & C is also 5 km.
Therefore, this relation is not equivalent.
|
181 videos|58 docs
|
FAQs on Types of Relations - Algebra - Mathematics
| 1. What is a relation in mathematics? |  |
| 2. What are the different types of relations in mathematics? |  |
| 3. How can we represent relations mathematically? |  |
| 4. What is the difference between a function and a relation? |  |
| 5. How can we determine if a relation is reflexive, symmetric, or transitive? |  |
















