Types of Unitary Method | SSC CGL Tier 2 - Study Material, Online Tests, Previous Year PDF Download
| Table of contents |

|
| Introduction |

|
| What is Unitary Method? |

|
| Types of Unitary Method |

|
| Unitary Method in Ratio and Proportion |

|
| Real-Life Applications of Unitary Method |

|
Introduction
The unitary method is a technique used to determine the value of a single unit based on the value of multiple units, and vice versa. This method is widely applied in various mathematical calculations, including those involving ratio and proportion, algebra, geometry, and more.
Utilizing the unitary method allows us to find missing values. For instance, if the cost of 1 packet of juice is $5, we can employ the unitary method to ascertain the cost of 5 such packets, which would amount to $25. This lesson will provide a detailed understanding of this concept.
What is Unitary Method?
Let's review the definition of the unitary method: "It is a technique where the value of a single unit is determined from the value of multiple units, and vice versa."
To illustrate this method, consider the following scenario: Emma visited an ice cream parlor and purchased 5 ice creams, paying $125 to the shopkeeper. The next day, she returned to the same parlor and ordered 3 ice creams. Calculating the cost for 3 ice creams might seem challenging at first, but we can simplify this problem using the unitary method.
Steps to Use Unitary Method
First, let us make a note of the information we have. There are 5 ice-creams. 5 ice-creams cost $125.
- Step 1: Let’s find the cost of 1 ice cream. In order to do that, divide the total cost of ice-creams by the total number of ice-creams. The cost of 1 ice-cream = Total cost of ice-creams/Total number of ice-creams = 125/5 = 25. Therefore, the cost of 1 ice cream is $25.
- Step 2: To find the cost of 3 ice-creams, multiply the cost of 1 ice cream by the number of ice-creams. The cost of 3 ice-creams is cost of 1 ice-cream × number of ice-creams = 25 × 3 = $75. Finally, we have the cost of 3 ice-creams i.e. $75.
In the unitary method, the value of many things is given and we need to either find the value of more or fewer things. In order to do that, we must first find the value of one thing by division and then find the value of more or fewer things by multiplication. 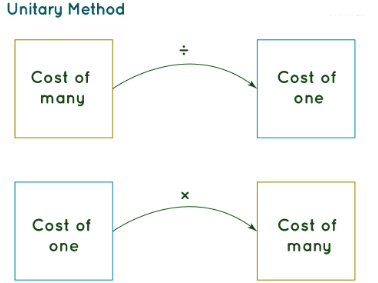
This diagram of the unitary method depicts that if we have to find the cost of 1 item from the given cost of many items, we apply division operation. While, if we have to find the cost of many items from the cost of 1 item, we apply multiplication operation.
Types of Unitary Method
Within the unitary method, our initial focus is consistently on determining the value of one unit or a single quantity. Subsequently, we extend this calculation to ascertain the values of additional or reduced quantities. This nomenclature, the unitary method, originates from this sequential approach. Two distinct types of unitary methods exist, each leading to different variations, as outlined below:
- Direct Variation
- Indirect Variation
Direct Variation in Unitary Method
This category delineates the straightforward correlation between two quantities. Put simply, when one quantity rises, the other also ascends, and conversely, when one quantity diminishes, the other also decreases. For instance, when the speed of a car elevates, it traverses a greater distance within a set timeframe. Thus, speed and distance exemplify a direct variation, showcasing their interdependence.
Indirect Variation in Unitary Method
This category characterizes the inverse correlation between two quantities. To put it plainly, when one quantity rises, the other falls, and conversely, when one quantity declines, the other rises. For instance, augmenting the speed of a car leads to covering a fixed distance in a shorter duration. Speed and time exemplify an indirect variation, illustrating their interrelationship.
Unitary Method in Ratio and Proportion
Unitary method in maths is also used to find the ratio between two quantities. Consider the following situation. A contractor employed two men, Ryan and David, to work in his factory and paid them daily wages. Ryan is paid $150 and David is paid $110 for each day's work. Ryan saves $800 per month and David saves $500 per month. Can you find the ratio of their monthly expenditure?
- Let’s find their monthly income by using the unitary method. Ryan’s wages for one day= $150. Ryan’s wages for one month= $(150 × 30) = $4500. Similarly, David’s wages for one month= $(110 × 30) = $3300.
- Now find their monthly expenditure. Ryan’s monthly expenditure = $4500 - $800 = $3700. David’s monthly expenditure = $3300 - $500 = $2800.
- The ratio of their monthly expenditure is given by, Ryan’s monthly expenditure/David’s monthly expenditure=3700/2800=37/28.
Proportion is defined as the relationship between two ratios. So, with the help of the unitary method, we can also find the missing value in the given proportion of two quantities. For example, if the cost and number of balloons sold by two different sellers are defined in a proportion as 3:4::15:x. Here we can find the missing value of x by using the concept of the unitary method. If the cost of 4 balloons is $3, then the number of balloons bought in $15 is 3/4 = 15/x, which is the same as, 3x=60. So, the number of balloons is 20.
Let's move on to solve some more real-life problems based on the unitary method.
Real-Life Applications of Unitary Method
The unitary method proves highly beneficial in resolving diverse problems encountered in our everyday experiences. Below are a few practical applications of the unitary method in real-life scenarios:
- To find the speed of an object for a given distance, if the speed and distance are given in different quantities.
- To find the number of people required to complete a given amount of work.
- To find the area of a square of a given length if the ratio of its area and side is given.
- To find the cost of a specific number of objects, if the cost and number of objects are given in different quantities.
- To find the percentage of a quantity.
Important Notes:
- The value of many quantities is found by multiplying the value of one quantity by the number of quantities.
- The value of one quantity is found by dividing the value of many quantities by the number of quantities.
Unitary Method Word Problems
Example 1: Ron goes to a stationery shop to buy some notebooks. The shopkeeper informs him that 2 notebooks would cost $90. Can you find the cost of 5 notebooks with the help of the unitary method?
Sol:
In this example, the number of books corresponds to the “unit” and the cost of the books corresponds to the “value”. Let's solve it step-wise.
Step 1: First, we will find the cost of 1 notebook. Cost of 1 notebook= Total cost of books/Total number of books= 90/2= $45.
Step 2: Now, we will find the cost of 5 notebooks. Cost of 5 notebooks= Cost of 1 book × Number of books= 45 × 5= 225.
Therefore, the cost of 5 notebooks is $225.
Example 2: Rachel can type 540 words in half an hour. How many words will she be able to type in 20 minutes with the same efficiency?
Sol:
The number of words typed in half an hour i.e. 30 min = 540. Therefore, by using the unitary method we can find the number of words typed in a minute.
Number of words typed in 1 min = 540/30=18.
Number of words typed in 20 min = 20 × 18 = 360.
Hence, Rachel will be able to type 360 words in 20 minutes.
|
1365 videos|1312 docs|1010 tests
|
FAQs on Types of Unitary Method - SSC CGL Tier 2 - Study Material, Online Tests, Previous Year
| 1. What is the concept of Unitary Method? |  |
| 2. What are the types of Unitary Method? |  |
| 3. How is Unitary Method used in Ratio and Proportion? |  |
| 4. Can you provide some real-life applications of Unitary Method? |  |
| 5. How can I practice and improve my skills in using the Unitary Method? |  |
|
1365 videos|1312 docs|1010 tests
|

|
Explore Courses for SSC CGL exam
|

|
















