Uniform Motion | Basic Physics for IIT JAM PDF Download
Linear motion, also called uniform motion or rectilinear motion, motion in one spatial dimension.
According to Newton’s first law (also known as the principle of inertia), a body with no net force acting on it will either remain at rest or continue to move with uniform speed in a straight line, according to its initial condition of motion. In fact, in classical Newtonian mechanics, there is no important distinction between rest and uniform motion in a straight line; they may be regarded as the same state of motion seen by different observers, one moving at the same velocity as the particle, the other moving at constant velocity with respect to the particle.
A body in motion may be said to have momentum equal to the product of its mass and its velocity. It also has a kind of energy that is entirely due to its motion, called kinetic energy. The kinetic energy of a body of mass m in motion with velocity v is given by K = (1/2)mv2.
Falling bodies and uniformly accelerated motion:
During the 14th century, the French scholar Nicole Oresme studied the mathematical properties of uniformly accelerated motion. He had little interest in whether that kind of motion could be observed in the realm of actual human existence, but he did discover that, if a particle is uniformly accelerated, its speed increases in direct proportion to time, and the distance it traverses is proportional to the square of the time spent accelerating. Two centuries later, Galileo repeated these same mathematical discoveries (perhaps independently) and, just as important, determined that this kind of motion is actually executed by balls rolling down inclined planes. As the incline of the plane increases, the acceleration increases, but the motion continues to be uniformly accelerated. From this observation, Galileo deduced that a body falling freely in the vertical direction would also have uniform acceleration. Even more remarkably, he demonstrated that, in the absence of air resistance, all bodies would fall with the same constant acceleration regardless of their mass. If the constant acceleration of any body dropped near the surface of Earth is expressed as g, the behaviour of a body dropped from rest at height z0 and time t = 0 may be summarized by the following: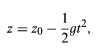 (4)
(4)
v = gt (5)
a= g (6)
where z is the height of the body above the surface, v is its speed, and a is its acceleration. These equations of motion hold true until the body actually strikes the surface. The value of g is approximately 9.8 metres per second squared (m/s2).
A body of mass m at a height z0 above the surface may be said to possess a kind of energy purely by virtue of its position. This kind of energy (energy of position) is called potential energy. The gravitational potential energy is given by
U = mgzo (7)
Technically, it is more correct to say that this potential energy is a property of the Earth-body system rather than a property of the body itself, but this pedantic distinction can be ignored.
As the body falls to height z less than z0, its potential energy U converts to kinetic energy K = 1/2mv2. Thus, the speed v of the body at any height z is given by solving the equation.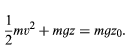 (8)
(8)
Equation (8) is an expression of the law of conservation of energy. It says that the sum of kinetic energy, 1/2mv2, and potential energy, mgz, at any point during the fall, is equal to the total initial energy, mgz0, before the fall began. Exactly the same dependence of speed on height could be deduced from the kinematic equations (4), (5), and (6) above.
In order to reach the initial height z0, the body had to be given its initial potential energy by some external agency, such as a person lifting it. The process by which a body or a system obtains mechanical energy from outside of itself is called work. The increase of the energy of the body is equal to the work done on it. Work is equal to force times distance.
The force exerted by Earth’s gravity on a body of mass m may be deduced from the observation that the body, if released, will fall with acceleration g. Since force is equal to mass times acceleration, the force of gravity is given by F = mg. To lift the body to height z0, an equal and opposite (i.e., upward) force must be exerted through a distance z0. Thus, the work done is
W = Fz0 = mgzo (9)
which is equal to the potential energy that results.
If work is done by applying a force to a body that is not being acted upon by an opposing force, the body is accelerated. In this case, the work endows the body with kinetic energy rather than potential energy. The energy that the body gains is equal to the work done on it in either case. It should be noted that work, potential energy, and kinetic energy, all being aspects of the same quantity, must all have the dimensions ml2/t2.
|
210 videos|156 docs|94 tests
|
FAQs on Uniform Motion - Basic Physics for IIT JAM
| 1. What is uniform motion in physics? |  |
| 2. How is uniform motion different from non-uniform motion? |  |
| 3. How can we calculate the average speed in uniform motion? |  |
| 4. Is it possible for an object to have a constant velocity but changing speed in uniform motion? |  |
| 5. Can an object be in uniform motion if it is moving in a curved path? |  |

|
Explore Courses for Physics exam
|

|


















