Units and Measurements, Chapter Notes, Class 11, Physics (IIT-JEE & AIPMT) PDF Download
System of Units and Fundamental Units - Units and Measurements, Class 11, Physics
Units and Measurements
1. PHYSICAL QUANTITY
The quantites which can be measured by an instrument and by means of which we can describe the laws of physics are called physical quantities.
Types of physical quantities :

1.1 Fundamental
Although the number of physical quantities that we measure is very large, we need only a limited number of units for expressing all the physical quantities since they are interrelated with one another. So, certain physical quantities have been chosen arbitrarily and their units are used for expressing all the physical quantities, such quantities are known as Fundamental, Absolute or Base Quantities (such as length, time and mass in mechanics)
(i) All other quantites may be expressed in terms of fundamental quantities.
(ii) They are independent of each other and cannot be obtained from one another.
An international body named General Conference on Weights and Measures chose seven physical quantities as fundamental :
(1) length (2) mass (3) time
(4) electric current, (5) thermodynamic temperature (6) amount of substance
(7) luminous intensity.
Note : These are also called as absolute or base quantities.
In mechanics, we treat length, mass and time as the three basic or fundamental quantities.
1.2 Derived : Physical quantities which can be expressed as combination of base quantities are called as derived quantities.
For example : Speed, velocity, acceleration, force, momentum, pressure, energy etc.
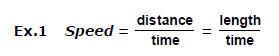
1.3 Supplementary : Beside the seven fundamental physical quantities two supplementary quantities are also defined, they are :
(1) Plane angle (2) Solid angle.
Note : The supplementary quantities have only units but no dimensions.
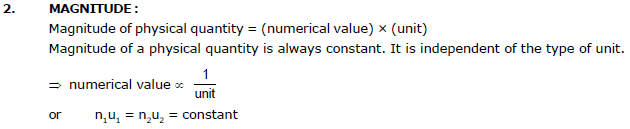
Ex.2 Length of a metal rod bar is unchanged whether it is measured as 2 metre or 200 cm.
Observe the change in the Numerical value (from 2 to 200) as unit is changed from metre to cm.
3. UNIT :
Measurement of any physical quantity is expressed in terms of an internationally accepted certain basic reference standard called unit.
The units for the fundamental or base quantities are called fundamental or base unit. Other physical quantities are expressed as combination of these base units and hence, called derived units.
A complete set of units, both fundamental and derived is called a system of unit.
3.1. Principle systems of Unit
There are various system in use over the world : CGS, FPS, SI (MKS) etc
Table 1 : Units of some physical quantities in different systems.

3.2 Supplementary units :
(1) Plane angle : radian (rad)
(2) Solid angle : steradian (sr)
* The SI system is at present widely used throughout the world. In IIT JEE only SI system is followed.
3.3 Definitions of some important SI Units
(i) Metre : 1 m = 1,650, 763.73 wavelengths in vaccum, of radiation corresponding to organ-red light of krypton-86.
(ii) Second : 1 s = 9,192, 631,770 time periods of a particular from Ceasium - 133 atom.
(iii) Kilogram : 1kg = mass of 1 litre volume of water at 4°C
(iv) Ampere : It is the current which when flows through two infinitely long straight conductors of negligible cross-section placed at a distance of one metre in vacuum produces a force of 2 × 10-7 N/m between them.
(v) Kelvin : 1 K = 1/273.16 part of the thermodynamic temperature of triple point of water.
(vi) Mole : It is the amount of substance of a system which contains as many elementary particles (atoms, molecules, ions etc.) as there are atoms in 12g of carbon - 12.
(vii) Candela : It is luminous intensity in a perpendicular direction of a surface of 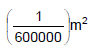 of a black body at the temperature of freezing point under a pressure of 1.013 × 105 N/m2.
of a black body at the temperature of freezing point under a pressure of 1.013 × 105 N/m2.
(viii) Radian : It is the plane angle between two radiia of a circle which cut-off on the circumference, an arc equal in length to the radius.
(ix) Steradian : The steradian is the solid angle which having its vertex at the centre of the sphere, cut-off an area of the surface of sphere equal to that of a square with sides of length equal to the radius of the sphere.

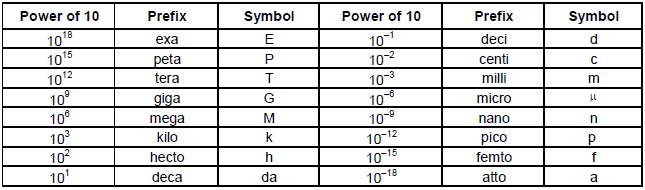
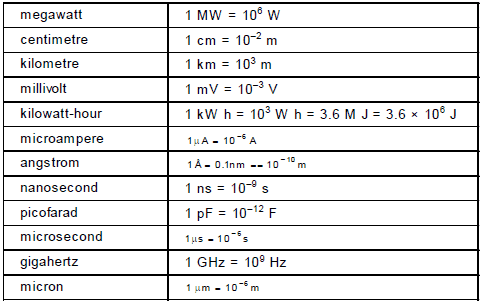
4. S.I Prefixes
The magnitudes of physical quantities vary order a wide range. The CGPM recommended standard prefixes for magnitude too large or too small to be expressed more compactly for certain power of 10.
5. General Guidelines for using Symbols for SI Units, Some other Units, and SI prefixes
(a) Symbols for units of physical quantities are printed/written in Roman (upright type), and not in italics
For example : 1 N is correct but 1 N is incorrect
(b) (i) Unit is never written with capital initial letter even if it is named after a scientist.
For example : SI unit of force is newton (correct) Newton (incorrect)
(ii) For a unit named after a scientist, the symbol is a capital letter.
But for other units, the symbol is NOT a capital letter.
For example :
force → newton (N)
energy → joule (J)
electric current → ampere (A)
temperature → kelvin (K)
frequency → hertz (Hz)
For example :
length → meter (m)
mass → kilogram (kg)
luminous intensity → candela (cd)
time → second (s)
Note : The single exception is L, for the unit litre.
(c) Symbols for units do not contain any final full stop all the end of recommended letter and remain unaltered in the plural, using only singular form of the unit.
For example :

(d) Use of solidus ( / ) is recommended only for indicating a division of one letter unit symbol by another unit symbol. Not more than one solidus is used.
For example :
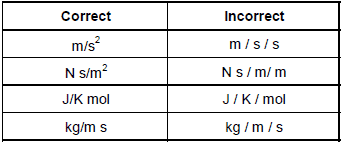
(e) Prefix symbols are printed in roman (upright) type without spacing between the prefix symbol and the unit symbol. Thus certain approved prefixes written very close to the unit symbol are used to indicate decimal fractions or multiples of a SI unit, when it is inconveniently small or large.
For example
The unit 'fermi', equal to a femtometre or 10-15 m has been used as the convenient length unit in nuclear studies.
(f) When a prefix is placed before the symbol of a unit, the combination of prefix and symbol is considered as a new symbol, for the unit, which can be raised to a positive or negative power without using brackets. These can be combined with other unit symbols to form compound unit.
For example :
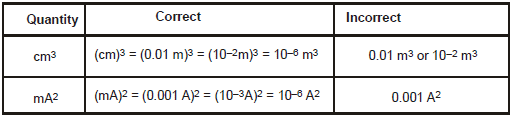
(g) A prefix is never used alone. It is always attached to a unit symbol and written or fixed before the unit symbol.
For example :
103/m3 = 1000/m3 or 1000 m-3, but not k/m3 or k m-3.
(h) Prefix symbol is written very close to the unit symbol without spacing between them, while unit symbols are written separately with spacing with units are multiplied together.
For example :

(i) The use of double profixes is avoided when single prefixes are available.
For example :

(j) The use of a combination of unit and the symbols for unit is avoided when the physical quantity is expressed by combining two or more units.

5.1. Characteristics of base units or standards :
(A) Well defined (B) Accessibility (C) Invariability (D) Convenience in use
5.2 Some special types of units :
1. 1 Micron (1μ) = 10-4 cm = 10-6 m (length)
2. 1 Angstrom (1 Å) = 10-8 cm = 10-10m (length)
3. 1 fermi (1f) = 10-13 cm = 10-15 m (length)
4. 1 inch = 2.54 cm (length)
5. 1 mile = 5280 feet = 1.609 km (length)
6. 1 atmosphere = 105 N/m2 = 76 torr = 76 mm of Hg pressure (pressure)
7. 1 litre = 10-3 m3 = 1000 cm3 (volume)
8. 1 carat = 0.0002 kg (weight)
9. 1 pound (Ib) = 0.4536 kg (weight)
===============================================
Dimensions (Formulae and Equations) - Units and Measurements, Class 11, Physics
6. Dimensions
Dimensions of a physical quantity are the power to which the fundamental quantities must be raised to represent the given physical quantity.
For example, density 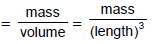
or density = (mass) (length)-3 ...(i)
Thus, the dimensions of density are 1 in mass and -3 in length. The dimensions of all other fundamental quantities are zero.
For convenience, the fundamental quantities are represented by one letter symbols. Generally mass is denoted by M, length by L, time by T and electric current by A.
The thermodynamic temperature, the amount of substance and the luminous intensity are denoted by the symbols of their units K, mol and cd respectively. The physical quantity that is expressed in terms of the base quantities is enclosed in square brackets.θ
[sinθ] = [cosθ] = [tanθ] = [ex] = [M0L0T0]
7. DIMENSIONAL FORMULA
It is an expression which shows how and which of the fundalmental units are required to represent the unit of physical quantity.
Different quantities with units. symbol and dimensional formula.


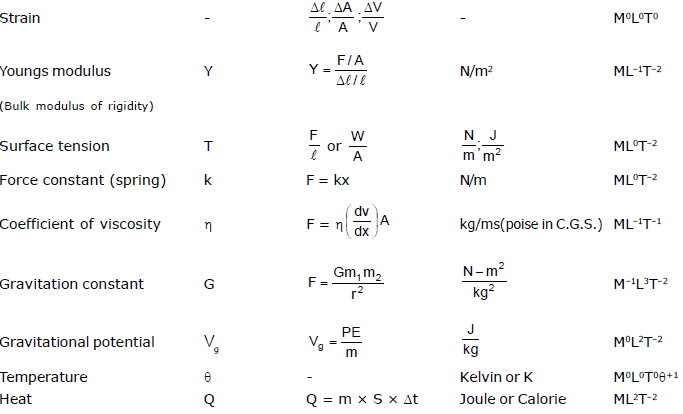


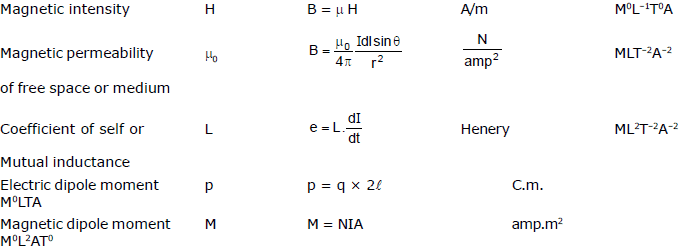
8. Use of Dimensions
Theory of dimensions have following main uses :
8.1 Conversion of units :
This is based on the fact that the product of the numerical value (n) and its corresponding unit (u) is a constant, i.e.,
n[u] = constant
or n1[u1] = n2 [u2]
Suppose the dimensions of a physical quantity are a in mass, b in length and c in time. If the fundamental units in one system are M1, L1 and T1 and in the other system are M2, L2 and T2 respectively. Then we can write.
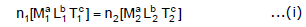
Here n1 and n2 are the numerical values in two system of units respectively. Using Eq. (i), we can convert the numerical value of a physical quantity from one system of units into the other system.
Ex.4 The value of gravitation constant is G = 6.67 × 10-11 Nm2/kg2 in SI units. Convert it into CGS system of units.
Sol. The dimensional formula of G is [M-1 L3 T-2].
Using equation number (i), i.e.,
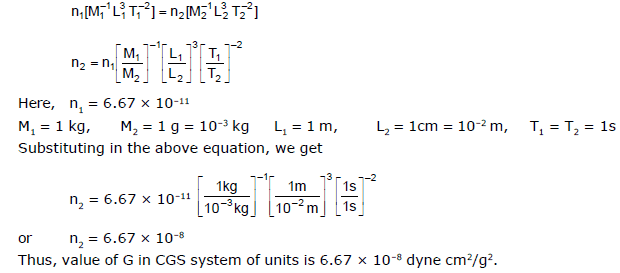
8.2 To check the dimensional correctness of a given physical equation :
Every physical equation should be dimensionally balanced. This is called the 'Principle of Homogeneity'. The dimensions of each term on both sides of an equation must be the same. On this basis we can judge whether a given equation is correct or not. But a dimensionally correct equation may or may not be physically correct.
Ex.5 Show that the expression of the time period T of a simple pendulum of length l given by T = 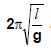 is dimensionally correct.
is dimensionally correct.
Sol.
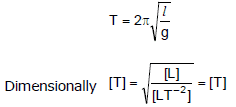
As in the above equation, the dimensions of both sides are same. The given formula is dimensionally correct.
8.3 Principle of Homogeneity of Dimensions.
This principle states that the dimensions of all the terms in a physical expression should be same. For example, in the physical expression  the dimensions of s, ut and
the dimensions of s, ut and  at2 all are same.
at2 all are same.
Note : The physical quantities separated by the symbols +, -, =, >, < etc., have the same dimensions.
Ex.6 The velocity v of a particle depends upon the time t according to the equation 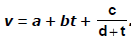 . Write the dimensions of a, b, c and d.
. Write the dimensions of a, b, c and d.
Sol.
From principle of homogeneity
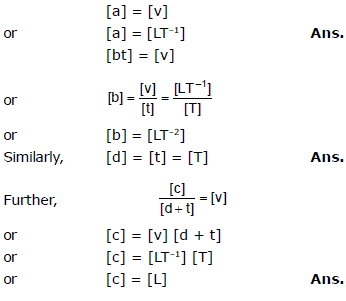
8.4 To establish the relation among various physical quantities :
If we know the factors on which a given physical quantity may depend, we can find a formula relating the quantity with those factors. Let us take an example.
Ex.7 The frequency (f) of a stretched string depends upon the tension F (dimensions of force), length l of the string and the mass per unit length m of string. Derive the formula for frequency.
Sol. Suppose, that the frequency f depends on the tension raised to the power a, length raised to the power b and mass per unit length raised to the power c. Then.
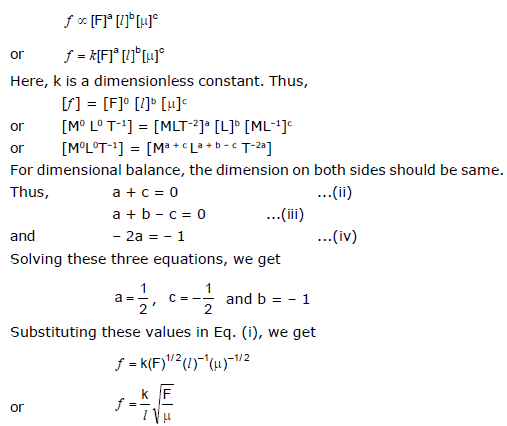
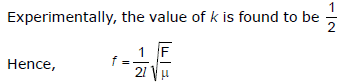
8.5 Limitations of Dimensional Analysis
The method of dimensions has the following limitations :
(i) By this method the value of dimensionless constant can not be calculated.
(ii) By this method the equation containing trigonometrical, exponential and logarithmic terms cannot be analysed.
(iii) If a physical quantity depends on more than three factors, then relation among them cannot be established because we can have only three equations by equalising the powers of M, L and T.
====================================================
BASIC MATHEMATICS
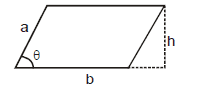
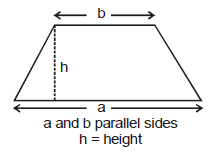
9. MENSURATION FORMULAS :
r : radius ; d = diameter ;
V = Volume S.A = surface area
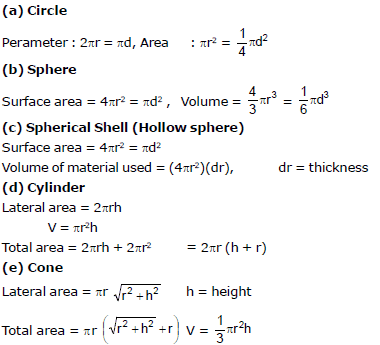
(f) Ellipse

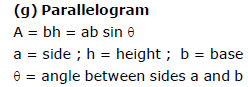
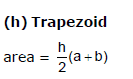

10. Logarithms :
(i) e ≈ 2.7183
(ii) If ex = y, then x = loge y = ln y
(iii) If 10x = y, then x = log10y
(iv) log10y = 0.4343 loge y = 2.303 log10y
(v) log (ab) = log (a) + log (b)
(vi)  = log(a) - log (b)
= log(a) - log (b)
(vii) log an = n log (a)
11. Trigonometric Properties :
(i) Measurement of angle & relationship between degrees & radian
In navigation and astronomy, angles are measured in degrees, but in calculus it is best to use units called radians because of they simplify later calculations.
Let ACB be a central angle in circle of radius r, as in figure.
Then the angle ACB or q is defined in radius as -
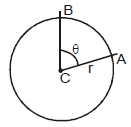
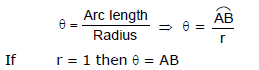
The radian measure for a circle of unit radius of angle ABC is defined to be the length of the circular arc AB. since the circumference of the cirlce is 2π and one complete revolution of a circle is 360°, the relation between radians and degrees is given by the following equation.
π radians = 180°
ANGLE CONVERSION FORMULAS≈
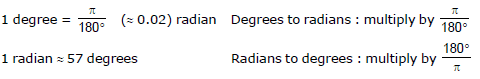
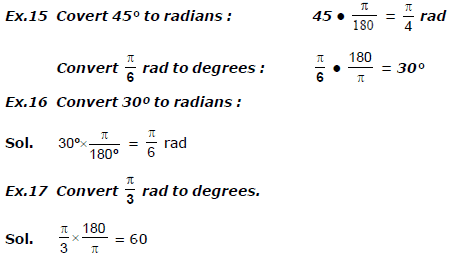

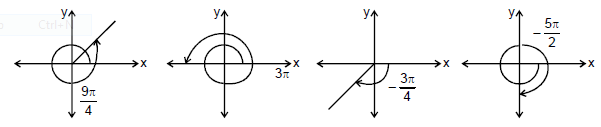
(ii) Measurement of positive & Negative Angles :


An angle in the xy-plane is said to be in standard position if its vertex lies at the origin and its initial ray lies along the positive x-axis (Fig). Angles measured counterclockwise from the positive x-axis are assigned positive measures; angles measured clockwise are assigned negative measures.

VALUES OF TRIGONOMETRIC FUNCTIONS
If the circle in (Fig. above) has radius r = 1, the equations defining sinθ and cosθ become
cosθ = x, sinθ = y
We can then calculate the values of the cosine and sine directly from the coordinates of P.

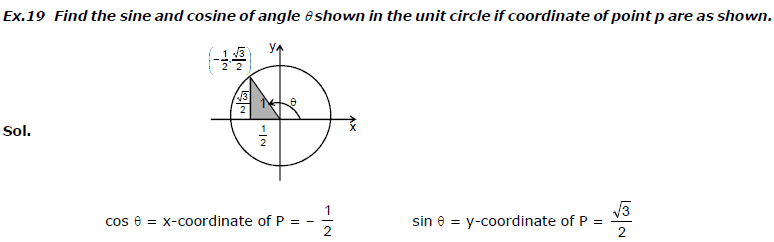
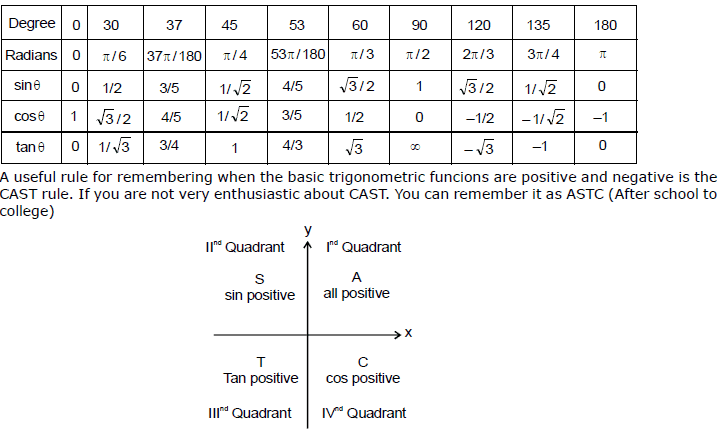
12. Values of sinθ, cosθ and tanθ for some standard angles.

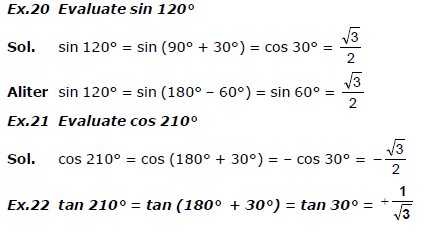
13. iMPORTANT FORMULAS
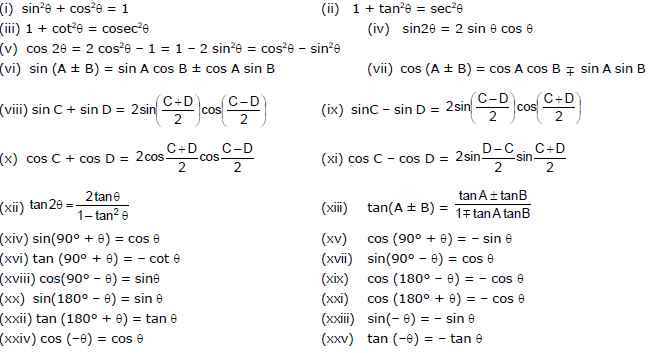
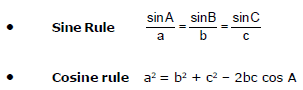
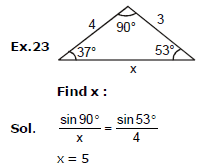
14. small angle approximation
It is a useful simplification which is only approximately true for finite angles. It involves linerarization of the trigonometric functions so that, when the angle q is measured in radians.
sinθ  θ
θ
cosθ  1 or cosθ
1 or cosθ  1 -
1 - 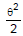 for the second - order approximation
for the second - order approximation
tanθ  q
q
Geometric justification
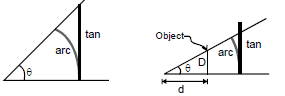
Small angle approximation. The value of the small angle X in radians is approximately equal to its tangent.
- When one angle of a right triangle is small, is hypotenuse in approximately equal in length to the leg adjacent to the small angle, so the cosine is approximately 1.
The short leg is approximately equal to the arc from the long leg to the hypotenuse, so the sine and tangent are both approximated by the value of the angle in radians.
15. BINOMIAL THEOREM :
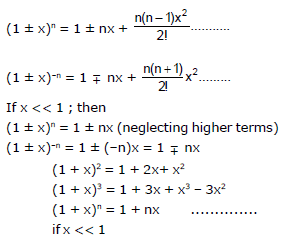
Note : (1) When n is a positive integer, then expansion will have (n + 1) terms
(2) When n is a negative integer, expansion will have infinite terms.
(3) When n is a fraction expansion will have infinite terms.
Ex. 24 Calculate (1001)1/3.
Sol.
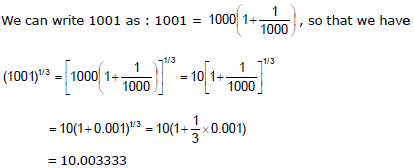
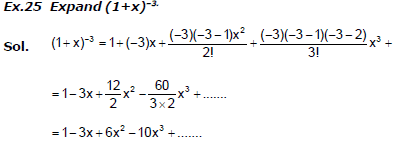
16. Graphs :
Following graphs and their corresponding equations are frequently used in Physics.
(i) y = mx, represents a straight line passing through origin. Here, m = tanθ is also called the slope of line, where θ is the angle which the line makes with positive x-axis, when drawn in anticlockwise direction from the positive x-axis towards the line.


The two possible cases are shown in figure 1.1 (i) θ< 90°. Therefore, tanθ or slope of line is positive. In fig. 1.1 (ii), 90° < θ < 180°. Therefore, tanθ or slope of line is negative.
Note : That y = mx of y ∞ x also means that value of y becomes 2 time if x is doubled. Or it becomes  if x becomes
if x becomes  and c the intercept on y-axis.
and c the intercept on y-axis.



In figure (i) : slope and intercept both are positive.
In figure (ii) : slope is negative but intercept is positive and
In figure (iii) : slope is positive but intercept is negative.
Note : That in y = mx + c, y does not become two times if x is doubled
Ex.26 v = u + at 
.
Ex.27 ρ = mv

Ex.28 Draw the graph for the equation : 2y = 3x + 2

Sol. 2y = 3x + 2 ⇒ y = 
m =  > 0 ⇒ θ < 90°
> 0 ⇒ θ < 90°
c = +1 > 0
⇒ The line will pass through (0, 1)
Ex.29 Draw the graph for the equation : 2y + 4x + 2 = 0
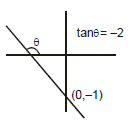
Sol. 2y + 4x + 2 = 0 ⇒ y = - 2x - 1
m = - 2 < 0 i.e., θ > 90°
c = - 1 i.e.,
line will pass through (0, -1)
 : (i) If c = 0 line will pass through origin.
: (i) If c = 0 line will pass through origin.
(ii) y = c will be a line parallel to x axis.

(iii) x = c will be a line perpendicular to y axis

(ii) Parabola
A general quadratic equation represents a parabola.
y = ax2 + bx + c a ¹ 0
if a > 0 ; It will be a opening upwards parabola.
if a < 0 ; It will be a opening downwards parabola.
if c = 0 ; It will pass through origin.
y ∞ x2 or y = 2x2, etc. represents a parabola passing through origin as shown in figure shown.
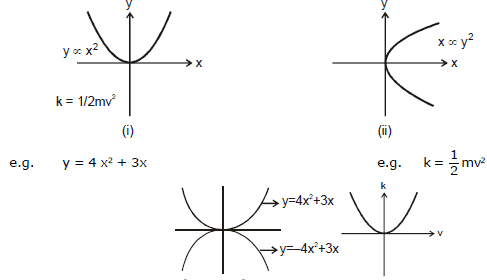
Note : That in the parabola y = 2x2 or y ∞ x2, if x is doubled, y will beome four times.
Graph x ∞ y2 or x = 4 y2 is again a parabola passing through origin as shown in figure shown. In this cae if y is doubled, x will become four times.
y = x2 + 4 or x = y2 - 6 will represent a parabola but not passing through origin. In the first equation
(y = x2 + 4), if x doubled, y will not become four times.
17. Similar Triangle
Two given triangle are said to be similar if
(1) All respective angle are same
or
(2) All respective side ratio are same.

As example, ABC, PQR are two triangle as shown in figure.
If they are similar triangle then
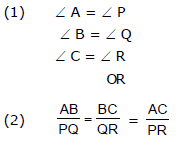
FAQs on Units and Measurements, Chapter Notes, Class 11, Physics (IIT-JEE & AIPMT)
| 1. What are the SI base units? |  |
| 2. What is the difference between accuracy and precision? |  |
| 3. How do you convert units within the SI system? |  |
| 4. What are some common prefixes used in the SI system? |  |
| 5. Why is it important to use standard units of measurement? |  |



















