Van der Waals equation and the theorem of corresponding states | Physical Chemistry PDF Download
Introduction
According to van der Waals, the theorem of corresponding states, it tells that all fluids, when compared at the same reduced temperature and reduced pressure, have approximately the same compressibility factor and all deviate from ideal gas behaviour to about the same degree.
Van der Waals equation
The ideal gas law treats gas molecules as point particles that interact with their containers but not each other, meaning they neither take up space nor change kinetic energy during collisions (i.e. all collisions are perfectly elastic). The ideal gas law states that volume (V) occupied by n moles of any gas has a pressure (P) at temperature (T) in kelvins given by the following relationship, where R is the gas constant: PV = n RT
To account for the volume that a real gas molecule takes up, the van der Waals equation replaces V in the ideal gas law with (Vm-b), where Vm is the molar volume of the gas and b is the volume that is occupied by one mole of the molecules. This leads to P(Vm - b) = RT
The second modification made to the ideal gas law accounts for the fact that gas molecules do in fact interact with each other (they usually experience attraction at low pressures and repulsion at high pressures) and that real gases, therefore, show different compressibility than ideal gases. Van der Waals provided for intermolecular interaction by adding to the observed pressure P in the equation of state a term
[P + a * (1/Vm^2)] [ (Vm - b)] = RT
Where a is a constant whose value depends on the gas. The van der Waals equation is therefore written as
[P + a*(n^2/V^2)] [ (V - nb)] = RT.
Where Vm is the molar volume of the gas, R is the universal gas constant, T is temperature, P is pressure, and V is volume. When the molar volume Vm is large, b becomes negligible in comparison with Vm, a/Vm2 becomes negligible with respect to P, and the van der Waals equation reduces to the ideal gas law, PVm = RT.
Theorem of corresponding states
The principle of Corresponding States (PCS) was stated by van der Waals and reads: “Substances behave alike at the same reduced states.”
Reduced properties: Reduced properties are used to define corresponding states. Reduced properties provide a measure of the “departure” of the conditions of the substance from its own critical conditions and are defined as follows:
Pr = P/Pc, Tr = T/Tc and Vr = V/Vc P, T and V are temperature, pressure and volume. Subscript c stands for critical point and r stands for reduced temperature and pressure. If Pr = Tr = Vr = 1, the substance is at its critical condition. If we are beyond critical conditions, Tr > 1, Pr > 1 and Vr > 1. By the same token, if all the conditions are subcritical, Tr < 1, Pr < 1 and Vr < 1. Critical conditions become the scaling factor by which substances can be compared among each other in terms of their “departure from criticality” or reduced properties.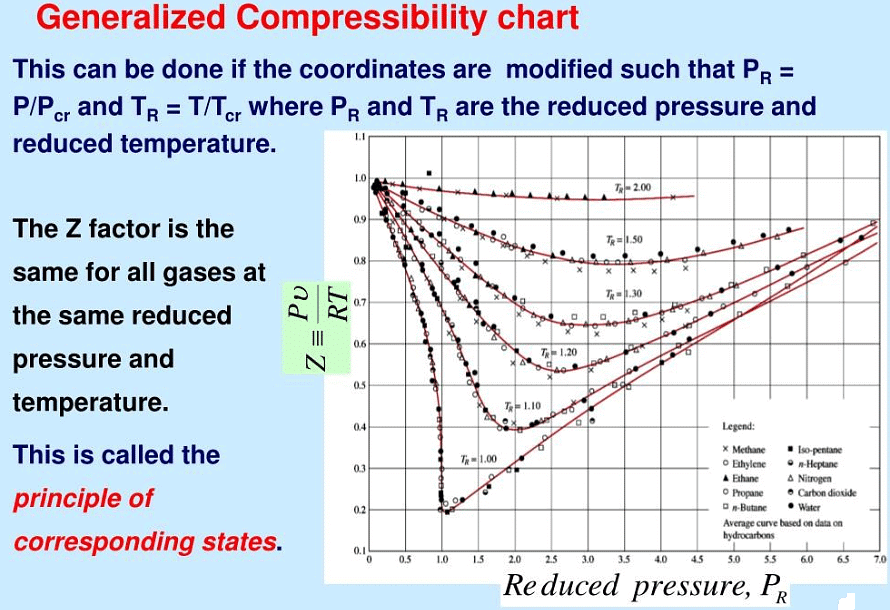
Compressibility factor at the critical point
The compressibility factor at the critical point, is defined as
Zc = Pc * Vc * Molar mass/ RTc , where the subscript c indicates the critical point, is predicted to be a constant independent of substance by many equations of state; the Van der Waals equation e.g. predicts a value of 3/8 = 0.375
The PCS says that all gases behave alike at the same reduced conditions. That is, if two gases have the same “relative departure” from criticality (i.e., they are at the same reduced conditions), the corresponding state principle demands that they behave alike. In this case, the two conditions “correspond” to one another, and we are to expect those gases to have the same properties.
Explanation
The Corresponding State Principle can be derived from van der walls EOS.
[P+ a*(n^2/V^2)] [ (V - nb)] = RT
Above equation reduces to reduced van der Walls EOS, [Pr*3/Vr^2] [3Vr - 1] = 8Tr
Above equation is the reduced form of van der Walls [vdW]EOS. This equation is “universal”. It does depend about which fluids we are talking about. Just give it the reduced conditions “Pr, Tr” and it will give you back Vr — regardless of the fluid. Hence, if you compute Vr for a certain fluid by entering Pr and Tr for that fluid into vdW reduced EOS, you will compute the same Vr, for any other fluid at the same conditions of Pr and Tr.
|
83 videos|142 docs|67 tests
|

|
Explore Courses for Chemistry exam
|

|

















