Variation of a functional - Calculus of Variations, CSIR-NET Mathematical Sciences | Mathematics for IIT JAM, GATE, CSIR NET, UGC NET PDF Download
II. First variation of functionals
The derivative of a function being zero is a necessary condition for the extremum of that function in ordinary calculus. Let us now tackle the question of the equivalent of a derivative for functionals because it plays the same crucial role in calculus of variations as does the derivative of the ordinary calculus in minimization of functions. Let us begin with a simple but a very important concept called a Gâteaux variation.
Gâteaux variation
The functional δJ (x) is called the Gâteaux variation of J at x w hen the limit that is defined as follows exists.
 where h is any vector in a vector space, X .
where h is any vector in a vector space, X .
Let us look at the meaning of h and ε geometrically. Note that x, h ∈X . Now, since x is the unknown function to be found so as to minimize (or maximize) a functional, we want to see what happens to the functional J ( x) when we perturb this function slightly. For this, we take another function h and multiply it by a small number ε . We add εh to x and look at the value of J (x + εh) . That is, we look at the perturbed value of the functional due to perturbation ε h . This is the shaded area shown in Fig. 1 where the function x is indicated by a thick solid line, h by a thin solid line, and x + ε h by a thick dashed line. Next, we think of the situation of ε tending to zero. As ε → 0 , we consider the limit of the shaded area divided by ε . If this limit exists, such a limit is called the Gâteaux variation of J (x) at x for an arbitrary but fixed vector h . Note that, we denote it as δJ (x;h) by including h in defining Gâteaux variation.
Figure 1. Pictorial depiction of variation ε h of a function x
Although the most important developments in calculus of variations happened in 17th and 18th centuries, this formalistic concept of variation was put forth by a French mathematician Gâteaux around the time of the first world war. So, one can say that intuitive and creative thinking leads to new developments and rigorous thinking makes them mathematically sound and completely unambiguous. To reinforce our understanding of the Gâteaux variation defined as above, let us relate it to the concept of a directional derivative in multi-variable calculus.
A directional derivative of the function f(x1,x2,xn) denoted in a compact form as  in the direction of a given vector
in the direction of a given vector is given by
is given by
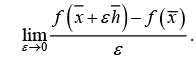
Here the “vector” is the usual notion that you know and not the extended notion of a “vector” in a vector space. We are using the over-bar to indicate that the denoted quantity consists of several elements in an array as in a column (or row) vector. You know how to take the derivative of a function 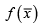 with respect to any of its variables, say xi , 1 ≤ i≤n. It is simply a partial derivative of
with respect to any of its variables, say xi , 1 ≤ i≤n. It is simply a partial derivative of 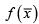 with respect to xi . You also know that this partial derivative indicates the rate of change of
with respect to xi . You also know that this partial derivative indicates the rate of change of 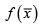 in the direction of xi . What if you want to know the rate of change of
in the direction of xi . What if you want to know the rate of change of 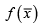 in some arbitrary direction denoted by
in some arbitrary direction denoted by 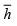 ? This is exactly what a directional derivative gives. Now, relate the concept of the directional derivative to Gâteaux variation because we want to know how the value of the functional changes in a “direction” of another element h in the vector space. Thus, the Gateaux variation extends the concept of the directional derivative of finite multi-variable calculus to infinite dimensional vector spaces, i.e., calculus of functionals.
? This is exactly what a directional derivative gives. Now, relate the concept of the directional derivative to Gâteaux variation because we want to know how the value of the functional changes in a “direction” of another element h in the vector space. Thus, the Gateaux variation extends the concept of the directional derivative of finite multi-variable calculus to infinite dimensional vector spaces, i.e., calculus of functionals.
Gâteaux differentiability
If Gateaux variation exists for all h ∈X then J is said to be Gateaux differentiable.
Operationally useful definition of Gâteaux variation
Gateaux variation can be thought of as the following ordinary derivative evaluated at ε = 0 .
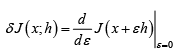
This helps calculate the Gâteaux variation easily by taking an ordinary derivative instead of evaluating the limit as in the earlier formal definition. Note that this definition follows from the earlier definition and the concept of how an ordinary derivative is defined in ordinary calculus if we think of the functional as a simple function of ε .
Gâteaux variation and the necessary condition for minimization of a functional
Gâteaux variation provides a necessary condition for a minimum of a functional.
Consider where J ( x ) , x ∈ D, is an open subset of a normed vector space X and x* ∈ D and any fixed vector h ∈X
If x* is a minimum, then
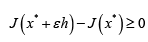
must hold for all sufficiently small ε
Now,
for ε≥0
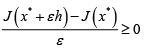
and for ε≤0
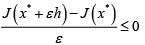
If we let ε→0,
and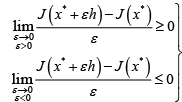
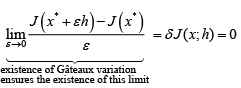
This simple derivation proves that the Gâteaux variation being zero is the necessary condition for the minimum of a functional. Likewise we can show (by simply reversing the inequality signs in the above derivation) that the same necessary condition applies to maximum of a functional.
Now, we can state this as a theorem since it is a very important result.
Theorem: necessary condition for a minimum of a functional
δ J x* ;h = 0 for all h∈ X
Based on the foregoing, we note that the Gâteaux variation is very useful in the minimization of a functional but the existence of Gateaux variation is a weak requirement on a functional since this variation does not use a norm in X . Thus, it is not directly related to the continuity of a functional. For this purpose, another differential called Fréchet differential has been put forth.
Frechet differential
If the above condition holds and dJ ( x; h ) is a linear, continuous functional of h , then J is said to be Fréchet differentiable at x with “increment” h .
dJ x; h ) is called the Fréchet differential.
If J is differentiable at each x ∈ D we say that J is Fréchet differentiable in D .
Some properties of Fréchet differential
i) J (x +h)= J (x) + dJ (x; h) + E (x; h) ║h║ for any small non-zero h ∈X has a limit zero at the zero vector in X . That is,
Based on this, sometimes the Fréchet differential is also defined as follows.
ii) dJ ( x; a1h1 + a2 h2 )= a1dJ ( x; h1) + a2 dJ ( x; h2 ) must hold for any numbers a1 ,a2 ∈ K and any h1 ,h2 ∈ X .
This is simply the linearity requirement on the Fréchet differential.
iii) dJ ( x; h ) ≤ constant h for all h∈ X
This is the continuity requirement on the Fréchet differential.
This is to say that the Fréchet differential is a linear functional of h . Note that it also introduces a new definition: Fréchet derivative, which is simply the coefficient of h in the Fréchet differential.
Relationship between Gâteaux variation and Fréchet differential
If a functional J is Fréchet differentiable at x then the Gateaux variation of J at x exists and is equal to the Fréchet differential. That is,
δ J x;h = dJ (x;h ) for all h∈ X
Here is why:
Due to the linearity property of dJ ( x; h ) , we can write
dJ (x;εh) =ε dJ (x; h)
Substituting the above result into property (i) of the Fréchet differential noted earlier, we get
J x +εh − J (x)−ε dJ (x;h) = E(x,ε h) ║h║ |ε| forany h∈ X
A small rearrangement of terms yields
When limit ε → 0 is taken, the above equation gives what we need to prove:
Note that the latter part of property (i) is once again used above.
Operations using Gateaux variation
Consider a simple general functional of the form shown below.
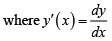
Note our sudden change of using x . It is no longer a member (element, vector) of a normed vector space X . It is now an independent variable and defines the domain of y (x) , which is a member of a normed vector space. Now, y(x) is the unknown function using which the functional is defined. We need to have our wits about you to see which symbol is used in what way!
If we want to calculate the Gâteaux variation of the above functional, instead of using the formal definition that needs an evaluation of the limit we should use the alternate operationally useful definition—taking the ordinary derivative of J ( y + εh ) with respect to ε and evaluating at ε = 0 . In fact, there is an easier route that is almost like a thumb-rule. Let us find that by using the derivative approach for the above simple functional.
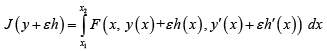
Recalling that 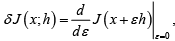 we can write
we can write
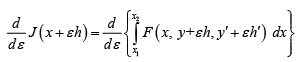
Please note that the order of differentiation and integration have been switched above. It is a legitimate operation. By using chain-rule of differentiation for the integrand of the above functional, we can further simplify it to obtain
What we have obtained above is a general result in that for any functional, be it of the form J (x, y, y′, y′′, y′′′,L) , we can write the variation as follows.
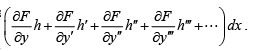
Note that in taking partial derivatives with respect to y and its derivatives we treat them as independent. It is a thumb-rule that enables us to write the variation rather easily by inspection and using rules of partial differentiation of ordinary calculus.
We have now laid the necessary mathematical foundation for deriving the Euler-Lagrange equations that are the necessary conditions for the extremum of a function. Note that the Gâteaux variation still has an arbitrary function h . When we get rid of this, we get the EulerLagrange equations. For that we need to talk about fundamental lemmas of calculus of variations.
|
558 videos|198 docs
|
FAQs on Variation of a functional - Calculus of Variations, CSIR-NET Mathematical Sciences - Mathematics for IIT JAM, GATE, CSIR NET, UGC NET
| 1. What is the calculus of variations? |  |
| 2. How is the calculus of variations related to the variation of a functional? |  |
| 3. What is the significance of the variation of a functional in the calculus of variations? |  |
| 4. What are some applications of the calculus of variations? |  |
| 5. How does the calculus of variations relate to the CSIR-NET Mathematical Sciences exam? |  |





















