Variational Principle - Approximate Methods of Quantum Mechanics, Physical Chemistry, CSIR-NET - Government Jobs PDF Download
The Variational Method
The variational method is the other main approximate method used in quantum mechanics. Compared to perturbation theory, the variational method can be more robust in situations where it's hard to determine a good unperturbed Hamiltonian (i.e., one which makes the perturbation small but is still solvable). On the other hand, in cases where there is a good unperturbed Hamiltonian, perturbation theory can be more efficient than the variational method.
The basic idea of the variational method is to guess a ``trial'' wavefunction for the problem, which consists of some adjustable parameters called ``variational parameters.'' These parameters are adjusted until the energy of the trial wavefunction is minimized. The resulting trial wavefunction and its corresponding energy are variational method approximations to the exact wavefunction and energy.
Why would it make sense that the best approximate trial wavefunction is the one with the lowest energy? This results from the Variational Theorem, which states that the energy of any trial wavefunction E is always an upper bound to the exact ground state energy ε0. This can be proven easily. Let the trial wavefunction be denoted  . Any trial function can formally be expanded as a linear combination of the exact eigenfunctions ψi. Of course, in practice, we don't know the ψi, since we're assuming that we're applying the variational method to a problem we can't solve analytically. Nevertheless, that doesn't prevent us from using the exact eigenfunctions in our proof, since they certainly exist and form a complete set, even if we don't happen to know them. So, the trial wavefunction can be written
. Any trial function can formally be expanded as a linear combination of the exact eigenfunctions ψi. Of course, in practice, we don't know the ψi, since we're assuming that we're applying the variational method to a problem we can't solve analytically. Nevertheless, that doesn't prevent us from using the exact eigenfunctions in our proof, since they certainly exist and form a complete set, even if we don't happen to know them. So, the trial wavefunction can be written
 (146)
(146)
and the approximate energy corresponding to this wavefunction is
 (147)
(147)
Substituting the expansion over the exact wavefuntions,
 (148)
(148)
Since the functions ψj are the exact eigenfunctions of  , we can use
, we can use 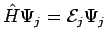 to obtain
to obtain
 (149)
(149)
Now using the fact that eigenfunctions of a Hermitian operator form an orthonormal set (or can be made to do so),
 (150)
(150)
We now subtract the exact ground state energy ε0 from both sides to obtain
 (151)
(151)
Since every term on the right-hand side is greater than or equal to zero, the left-hand side must also be greater than or equal to zero, or
![\begin{displaymath}
E[\Phi] \geq {\cal E}_0.
\end{displaymath}](https://cn.edurev.in/ApplicationImages/Temp/6d19ae51-178c-4f77-9ce3-c847a70b0d53_lg.png) (152)
(152)
In other words, the energy of any approximate wavefunction is always greater than or equal to the exact ground state energy ε0. This explains the strategy of the variational method: since the energy of any approximate trial function is always above the true energy, then any variations in the trial function which lower its energy are necessarily making the approximate energy closer to the exact answer. (The trial wavefunction is also a better approximation to the true ground state wavefunction as the energy is lowered, although not necessarily in every possible sense unless the limit  is reached).
is reached).
One example of the variational method would be using the Gaussian function 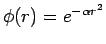 as a trial function for the hydrogen atom ground state. This problem could be solved by the variational method by obtaining the energy of φ(r) as a function of the variational parameter
as a trial function for the hydrogen atom ground state. This problem could be solved by the variational method by obtaining the energy of φ(r) as a function of the variational parameter 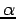 , and then minimizing E(α) to find the optimum value αmin. The variational theorem's approximate wavefunction and energy for the hydrogen atom would then be
, and then minimizing E(α) to find the optimum value αmin. The variational theorem's approximate wavefunction and energy for the hydrogen atom would then be 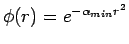 and E(αmin).
and E(αmin).
Frequently, the trial function is written as a linear combination of basis functions, such as
 (153)
(153)
This leads to the linear variation method, and the variational parameters are the expansion coefficients Ci. The energy for this approximate wavefunction is just
 (154)
(154)
which can be simplified using the notation
 (155), (156)
(155), (156)
to yield
 (157)
(157)
Differentiating this energy with respect to the expansion coefficients Ci yields a non-trivial solution only if the following ``secular determinant'' equals 0.
 (158)
(158)
If an orthonormal basis is used, the secular equation is greatly simplified because Sij is 1 for i=j and 0 for i≠j . In this case, the secular determinant is
 (159)
(159)
In either case, the secular determinant for N basis functions gives an N-th order polynomial in E which is solved for N different roots, each of which approximates a different eigenvalue.
The variational method lies behind Hartree-Fock theory and the configuration interaction method for the electronic structure of atoms and molecules.
FAQs on Variational Principle - Approximate Methods of Quantum Mechanics, Physical Chemistry, CSIR-NET - Government Jobs
| 1. What is the variational principle in quantum mechanics? |  |
| 2. How are approximate methods used in quantum mechanics? |  |
| 3. What is the role of the variational principle in physical chemistry? |  |
| 4. How can the variational principle be applied to CSIR-NET exam questions? |  |
| 5. Are there government job opportunities for individuals with expertise in quantum mechanics and approximate methods? |  |





















