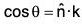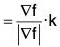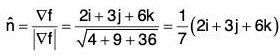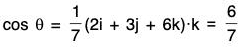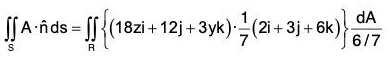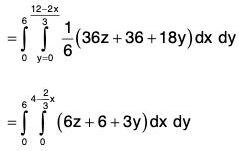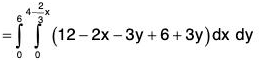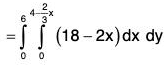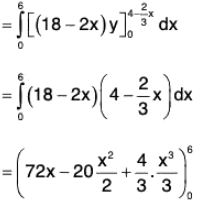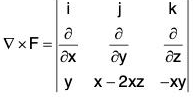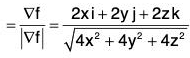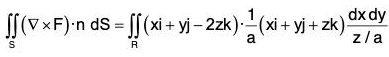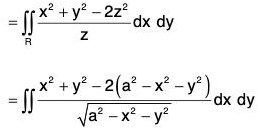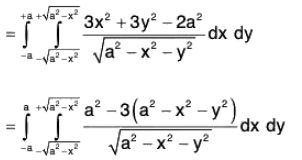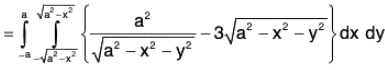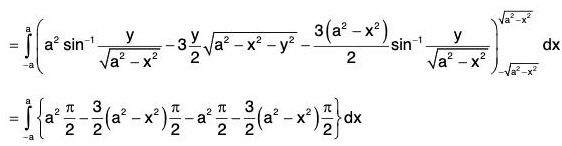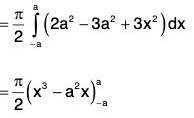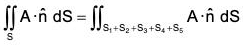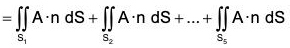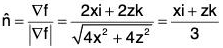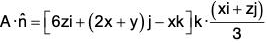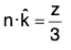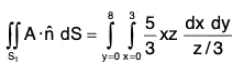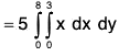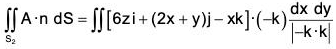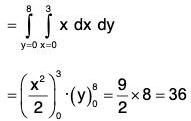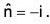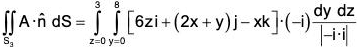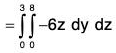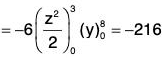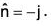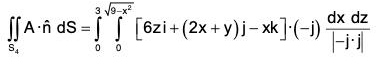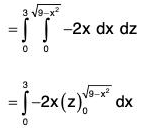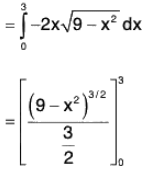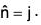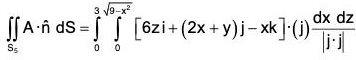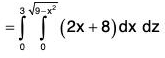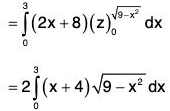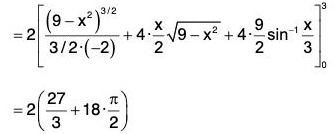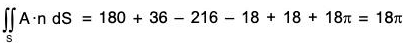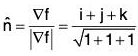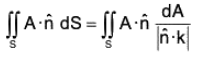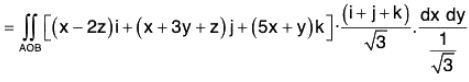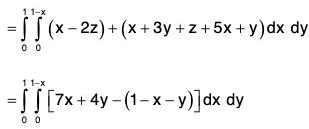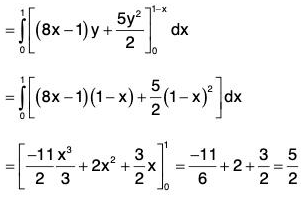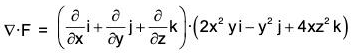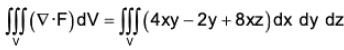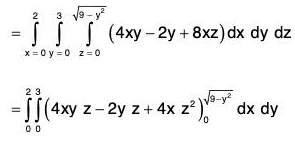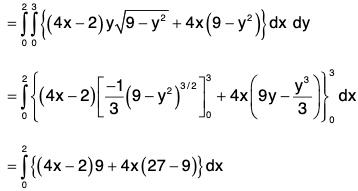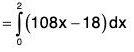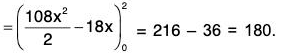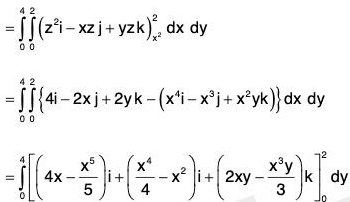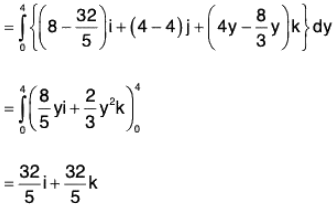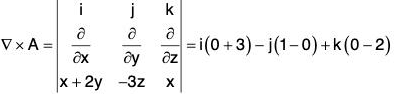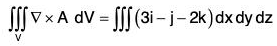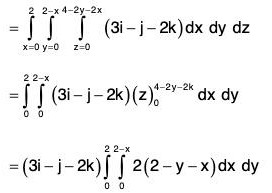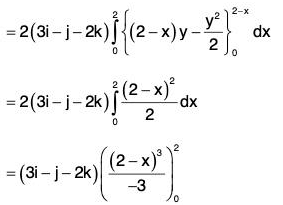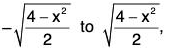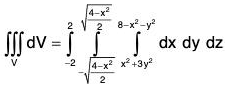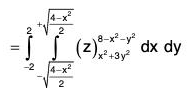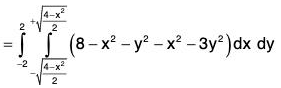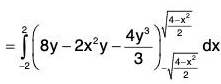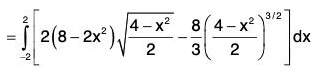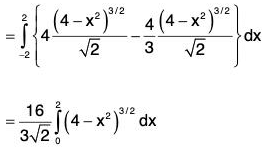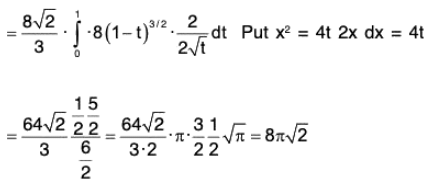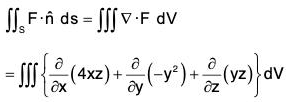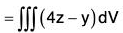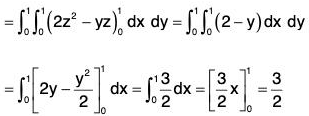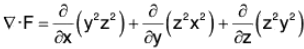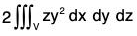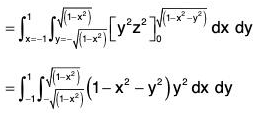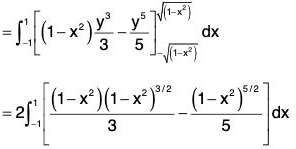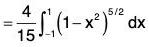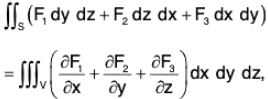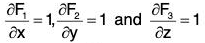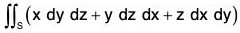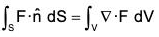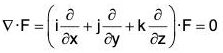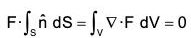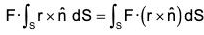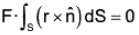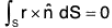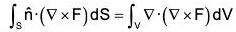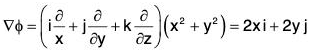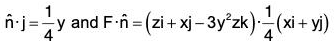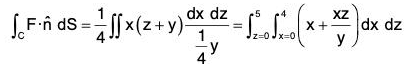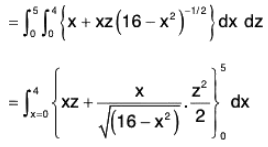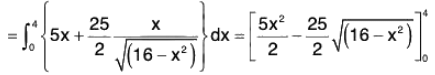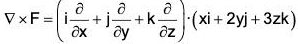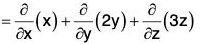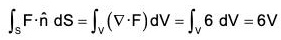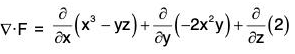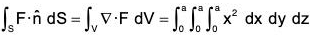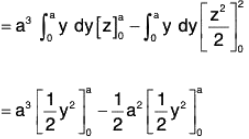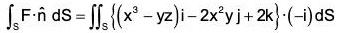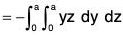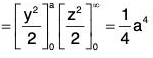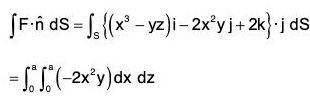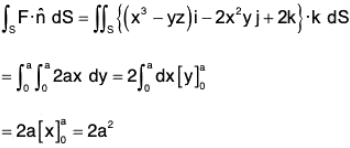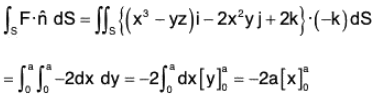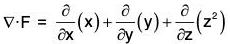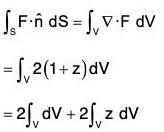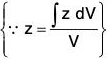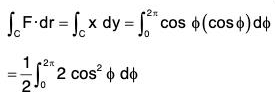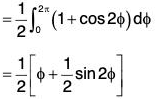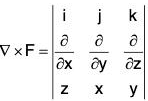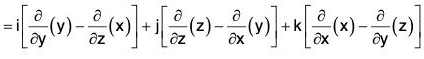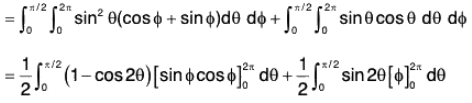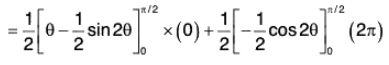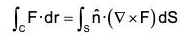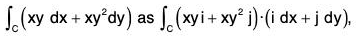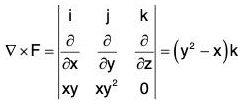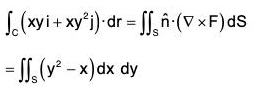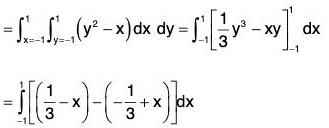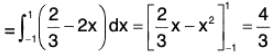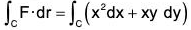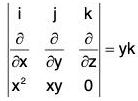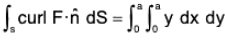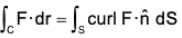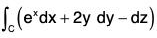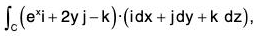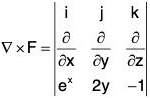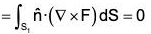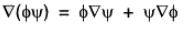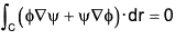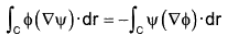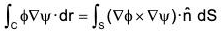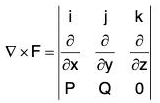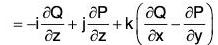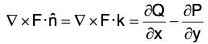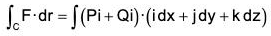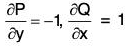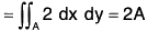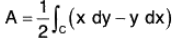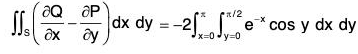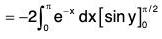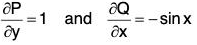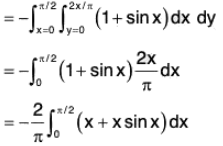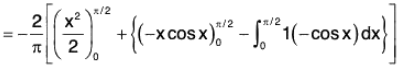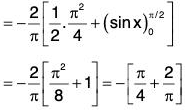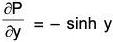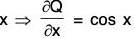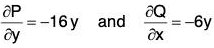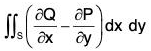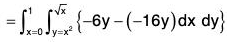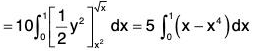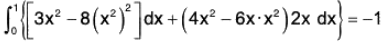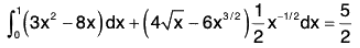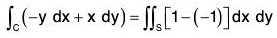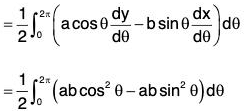Vector Calculus - (Part - 2) | Mathematics for Competitive Exams PDF Download
| Table of contents |

|
| Surface Area And Surface Integrals |

|
| Volume Integral |

|
| Gauss's Divergence Theorem |

|
| Stoke's Theorem |

|
| Green's Theorem |

|
Surface Area And Surface Integrals
A smooth surface S is called Orientable or two sided if it is possible to define a field n of unit normal vectors on S that varies continuously with position. Spheres and their smooth closed surface in space are orientable. By convention, we choose n on a closed surface to point outward.
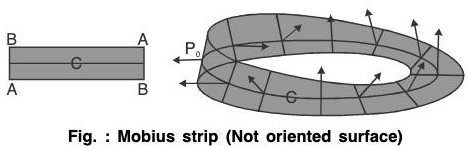
The surface together with its normal field is called oriented surface. Unit normal is at any point of it is called the positive direction at the point.
Let f(x, y, z) = c be any oriented surface S and R be its projection (Shadow) on coordinate plane (say xy-plane)
The angle between S and R is given by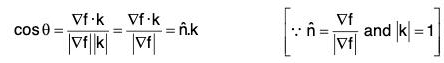
{z-axis is normal to xy-plane}
area of the surface f(x, y, z) = c over a closed and bounded plane region R is
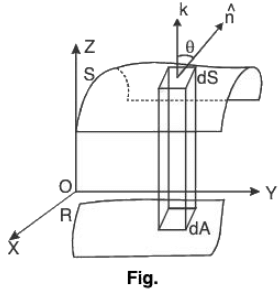 dS cos θ = dA
dS cos θ = dA
⇒ 
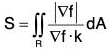
Surface Integral
If R be the projection (shadow) on xy-plane of surface S defined by equation f(x, y, z) = c and g is a continuous function defined at the points of S, then the integral of g over S is the integral.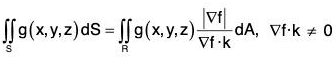
Suppose that F is a continuous vector field defined over an oriented surface S and that 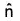 is unit normal to the surface S. The surface integral of the normal component of F, i.e. F.
is unit normal to the surface S. The surface integral of the normal component of F, i.e. F. 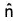 , is the flux of F across A in the positive direction and is given by
, is the flux of F across A in the positive direction and is given by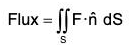
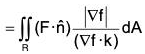
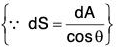

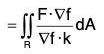 (∇ f.k ≠ 0)
(∇ f.k ≠ 0)
Remark :
(a) To find the surface integral of a vector function or flux means the same thing.
(b) If S is a surface defined by a function z = f(x, y) that has continuous first order partial derivatives throughout a region R in the xy-plane then
Let φ(x, y, z) = f(x, y) - z be the level surface
(a) Unit normal to φ(x, y, z) is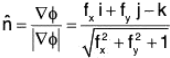
(b) Area of surface S is
Example : Evaluate 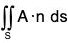 where A = 18zi + 12j + 3yk and S is the part of the plane 2x + 3y + 6z = 12 which is located in the first octant.
where A = 18zi + 12j + 3yk and S is the part of the plane 2x + 3y + 6z = 12 which is located in the first octant.
We know that ds = dA/cosθ
where θ is angle between the normal to surface S and normal to its projection in xy-plane
∴
S : f(x, y, z) = 2x + 3y + 6z - 12
∴
Now
= 432 - 360 + 96
= 72 + 96 = 168
Example : Evaluate : 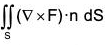 where F = yi + (x - 2xz)j - xyk and S is the surface of the sphere x2 + y2 + z2 = a2 above the xy-plane.
where F = yi + (x - 2xz)j - xyk and S is the surface of the sphere x2 + y2 + z2 = a2 above the xy-plane.
F = yi + (x - 2xz)j - xyk
= i (-x + 2x) - j (-y - 0) + k(1 - 2z - 1)
= xi + yj - 2zk ...(i)
Let S be the surface given by f(x, y, z) = x2 + y2 + z2 - a2 above xy-plane.
Thus, the projection on xy-plane is the circle x2 + y2 = a2. Also= unit normal to surface S
= (1/a)(xi + yj + zk) ...(ii)
and...(iii)
Now
= π/2(a3 - a3 + a3 - a3) = 0
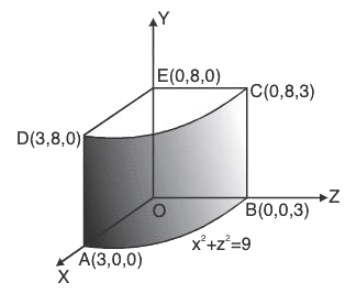
Example : Evaluate : 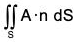 over the entire surface S of the region bounded by the cylinder x2 + z2 = 9, x = 0, y = 0, z = 0 and y = 8 where A = 6zi + (2x + y)j - xk.
over the entire surface S of the region bounded by the cylinder x2 + z2 = 9, x = 0, y = 0, z = 0 and y = 8 where A = 6zi + (2x + y)j - xk.
Here the entire surface S consists of 5 surfaces, namely. S1 : lateral surface of the cylinder ABCD, S2 : AOED, S3 : OBCE, S4 : OAB, S5 : CDE.
Thus,
= l1 + l2 + l3 + l4 + l5(say)
S1 : ABCD : The curved surface S1 is f = x2 + z2 = 9. The unit outward normal to S1 is
∴
= 1/3(6xz - xz) = (5/3)xz
and
∴
= (5 x 9 x 8)/2 = 180
S2 : AOED : The surface S2 is xy-plane i.e. z = 0. Unit outward normal to the surface is
∴
S3 : OBCE : Surface S3 is yz-plane i.e. x = 0. Unit outward normal to S3 is
∴
S4 : OAB : The section OAB is in xz-plane i.e. y = 0. The unit outward normal to S4 is
∴
= (2/3)(-27) = -18
S5 : CDE : The section S. is parallel to xz-plane, y = 8. The unit outward normal to S5 is
= 18(1+π)
Thus, the required surface integral is
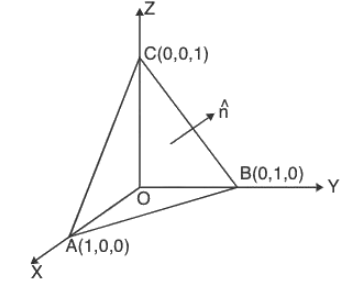
Example : Find the flux of the vector field A = (x - 2z)i + (x + 3y + z)j + (5x + y)k through the upper side of the triangle ABC with vertices at the points A(1, 0, 0), B(0, 1, 0) and C(0, 0, 1).
Equation of the plane containing the given triangle ABC is f(x, y, z) ≡ x + y + z - 1
Unit normal h to ABC is= (1/√3) (i + j + k)
Flux of A =
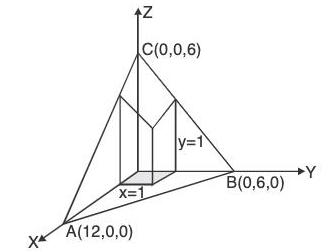
Example : Find the surface area of the plane 2z + x + 2y = 12 cut off by x = 0, y = 0, x = 1, Y = 1.
Let φ(x, y, z) = ((12 - x - 2y)/2)-z = 0 be the level surface.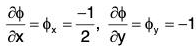
∴ 
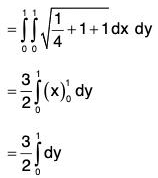
= (3/2)(y)10
= 3/2
Volume Integral
Let V be a region is space enclosed by a closed surface S. Let F be a vector point function, and φ be a scalar point function, then the triple integrals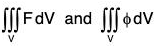 are known as volume integral or space integrals.
are known as volume integral or space integrals.
In component form 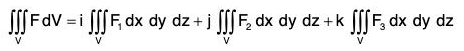
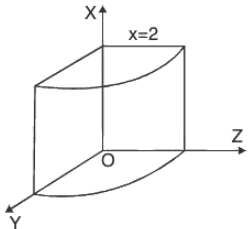
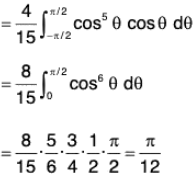
Example : If V is the region of first octant bounded by y2 + z2 = 9 and the plane x = 2 and F = 2x2 yi - y2 j + 4xz2k. Then evaluate 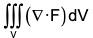
= 4xy - 2y + 8xz
Example : If F = 2z i + xj + yk. Evaluate 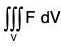 where V is the region bounded by the surfaces x = 0, y = 0, x = 2, y = 4, z = x2, z = 2.
where V is the region bounded by the surfaces x = 0, y = 0, x = 2, y = 4, z = x2, z = 2.
= 32/15(3i + 5k)
Example : Evaluate 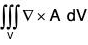 where A = (x + 2y)i - 3z j + xk and V is the closed region in the first octant bounded by the plane 2x + 2y + z = 4
where A = (x + 2y)i - 3z j + xk and V is the closed region in the first octant bounded by the plane 2x + 2y + z = 4
= 3i - j - 2k
= (8/3)(3i - j - 2k)
Example : Find the volume enclosed between the two surfaces S1 : z = 8 - x2 - y2 and S2 : z = x2 + 3Y2.
Eliminating z from the two surfaces S1 and S2, we get
8 - x2 - y2 = x2 + 3y2
⇒ x2 + 2y2 = 4
Thus, the two surface intersect on the elliptic cylinder.
So the solid region between S1 and S2 is covered when z varies from x2 + 3y2 to 8 - x2 - y2.
y varies from
x varies from - 2 to 2.
∴
Gauss's Divergence Theorem
Statement : The normal surface integral of a function F over the boundary of a closed region is equal to the volume integral of div F taking throughout the region.
If F is a continuously differentiable vector point function in a region V enclosed by the closed surface S, then :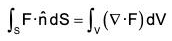 ...(1)
...(1)
where 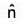 is the unit outward drawn normal vector to the surface S.
is the unit outward drawn normal vector to the surface S.
The Cartesian form of (1) is as follows :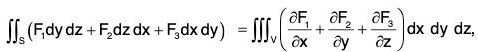 ...(2)
...(2)
where F1, F2 and F3 are scalar components of F along the axes.
Remark : The volume integral is reduced into surface integral with the help of this theorem. Conversely, the surface integral can also be reduced into volume integral.
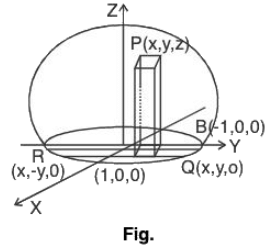
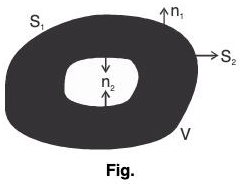
Proof. Let V be the region wrt the axes such that if any straight line is drawn parallel to any axis, then that will meet the surface S in two points only.
In fig., A3 is the projection of region V on the plane XOY. Let the coordinates of any point R in the plane A3 be (x, y, 0).
Let any line through R meets the surfaces at the points P and Q.
Therefore z-co-ordinate of Q by ψ(x, y) and that of P be φ(x, y).
Since RP > RQ, therefore φ(x, y) > ψ(x, y)
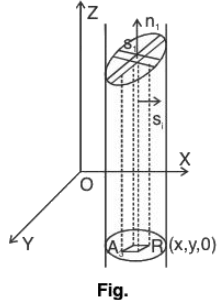
Now 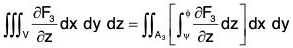
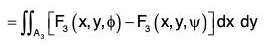
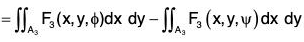 ...(3)
...(3)
Let S1 and S2 be the sub-parts of the surface S.
Let 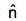 be the outwards drawn unit normal vector at any point on the surface S.
be the outwards drawn unit normal vector at any point on the surface S.
Therefore dx dy = dS cos θ = 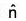 .k dS,
.k dS,
where θ is the angle of the normal with x-axis.
∴ 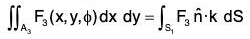 ...(4)
...(4)
and 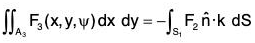 ...(5)
...(5)
The negative sign of equation (5) shows that the normal drawn outwards make an obtuse angle with z-axis.
The positive sign in equation (4) is because the outwards normal on the surface S1 make an acute angle with z-axis.
Substituting the value from the equations (4) and (5) in (3)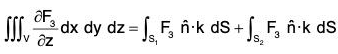
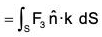 ...(6)
...(6)
Similarly,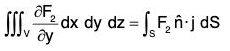 ...(7)
...(7)
and  ...(8)
...(8)
Adding the equations (6), (7) and (8),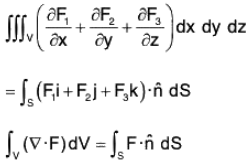
This theorem is also true for the region V enclosed by two closed curves S1 and S2, where the surface S2 is situated in side the surface S1.
Remark : The volume integral is reduced into surface integral with the help of this theorem. Conversely, the surface integral can also be reduced into volume integral.
Example : Evaluate : 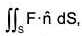 where F = 4xz i - y2j + yz k S is the surface of the cube bounded by the planes :
where F = 4xz i - y2j + yz k S is the surface of the cube bounded by the planes :
By Gauss’s theorem,
[∵ dv = dx dy dz]
Example : Evaluate : 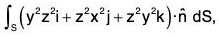 where S is the part of the sphere x2 + y2 + z2 = 1 above the xy plane.
where S is the part of the sphere x2 + y2 + z2 = 1 above the xy plane.
F = y2z2i + z2x2j + z2y2k
∴
= 2zy2
By Gauss’s theorem,
This is the part of the sphere x2 + y2 + z2 = 1 above the xy plane i.e., hemisphere above the xy plane and the limits for x, y, z are as follows :
First integrate wrt z from z = 0 to z =then integrate wrt y, between the limit
and finally wrt x between the limits x = -1 to x = 1.
∴ Required integral =
put x = sin θ ⇒ dx = cosθ dθ
Example : Use Gauss’s divergence theorem to show that :
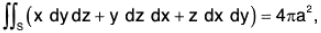 where the surface S is the sphere x2 + y2 + z2 = a2.
where the surface S is the sphere x2 + y2 + z2 = a2.
We know that
where F1 = x, F2 = y, and F3 = z
∴
∴ From equation (1)(1 + 1 + 1)dx dy dz, enclosed by surface S, where V is volume.
dx dy dz = 3 (volume of the sphere)
= 3.(4/3)πa2 = 4πa3
Example : If V is the volume enclosed by any closed surface S; show that:
(a) 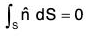
(b) 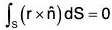
(c) 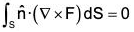
(d) 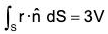
(a) If F be any constant vector, then
[∵ F is a constant vector]
By Gauss's theorem,
But
or,[∵ F is a constant vector]
(b) If F be any constant vector, then(by interchanging the scalar and vector products)
[by Gauss’s theorem] ...(1)
But ∇.(F x r) = r.(∇ x F) - F.(∇ x r) = 0 [∵ V x f = 0, ∵ F is constant and ∇ x r = 0]
By (1),
or,
(c) By Gauss’s theorem,
= 0 [∵ ∇.(Z∇ x F) = 0]
(d) By Gauss’s theorem,(∵ ∇.r = 3)
= 3V
Example : Evaluate : 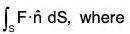 F = zi + xj + 3y2z k, where S is the surface of the cylinder x2 + y2 = 16 include in the first octant between z = 0 and z = 5.
F = zi + xj + 3y2z k, where S is the surface of the cylinder x2 + y2 = 16 include in the first octant between z = 0 and z = 5.
The projection of the given surface on xz plane will be a rectangle whose sides will be x, z axes and lines parallel to these.
Therefore the given integral...(1)
Normal vector on the given surface x2 + y2 = 16
∴
∴
= 1/4(xz + xy)
Now by (1),
= 5 x 8 - (25/2)(0 - 4) = 90
Example : If V is the volume enclosed by any closed surface S; show that : 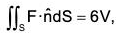 where F = xi + 2yj + 3zk
where F = xi + 2yj + 3zk
Given F = xi + 2yj + 3zk
∴
= 1 + 2 + 3 = 6
∴ By Gauss’s theorem,
Example : Verify Gauss’s Divergence theorem and show that :
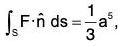 where F = (x3 - yz)i - 2x2yj + 2k S is the surface of the cube bounded by the co-ordinate planes : x = y = z = 0; x = y = z = a
where F = (x3 - yz)i - 2x2yj + 2k S is the surface of the cube bounded by the co-ordinate planes : x = y = z = 0; x = y = z = a
Here
= 3x2 - 2x2 + 0 = x2
∴
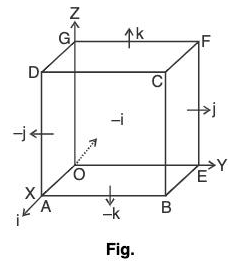
Verification by direct Integration : In figure outward unit normal have been shown on each face of the cube. Now on the face ABCD= i, x = a, dS = dy dz
(∵ x = a)
= a5 - (1/4)a4
Taking= - i on the face OEFC,
∴ On this face x = 0
Taking= j on the face BEFC.
[∵ on this face y = a]
Taking
= k on the face CDGF,
Taking= -k on the face ABEO,
= -2x2
Adding the integrals on all the faces,
= a5 - (1/4)a4 + (1/4)a4 - (2/3)a5 + 0 + 2a2 - 2a2
= (1/3)a5
Example : Evaluate : 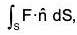 where F = xi + yj + z2k. where S is the closed surface bounded by the cone x2 + y2 = z2 and the plane z = 1.
where F = xi + yj + z2k. where S is the closed surface bounded by the cone x2 + y2 = z2 and the plane z = 1.
Here
= 1 + 1 + 2z = 2(1 + z)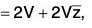
where V is the volume of the given cone and
is the centre of gravity of the cone (situated on the axis of the one) which is at a distance y from the vertex O. The base of the given cone is a circle whose radius is 1 and height is also 1.
∴ OG = 3/4, V = (1 /3)π12 . 1 = π/3
∴ Required integral = 2V(1 +)
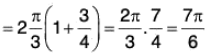
Stoke's Theorem
Statement : The line integral of a vector function F around any closed curve is equal to the surface integral of curl F taken over any surface of which of the curve is a boundary edge.
If F be any continuous differentiable vector function and S is the surface enclosed by a curve C, then :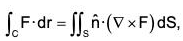
where n is the unit normal vector at any point of S and drawn in the sense in which a right handed screw would move rotated in the sense of description of C.
Cartesian form :
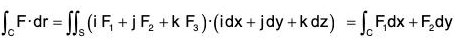 [∵ dz = 0]
[∵ dz = 0]
Since 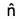 = k, therefore
= k, therefore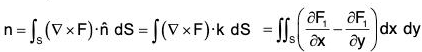
Proof, (a) For surfaces in the planes :
Let the region S1 be subdivided into sub-regions Si such that if a straight line is drawn parallel to any axis then that will meet the curve Ci atmost in two points.
Let Ci be situated between the lines x = a and x = b.
Let any line the be drawn parallel to y-axis meets the curve at the point P and Q, where the ordinate of P is y = φ(x) and that of Q is y = ψ(x). In the figure limit of the curve has been divided by the line PQ in two parts C1 and C2
Now,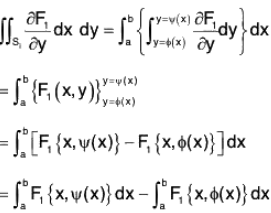
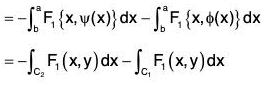
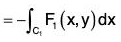 ...(1)
...(1)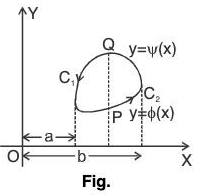
Similarly, 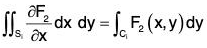 ...(2)
...(2)
From (1) and (2),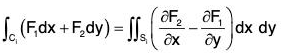
or, 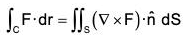
(b) The Cartesian form of the surface in space,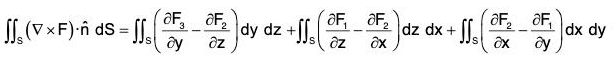
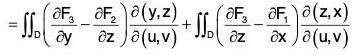
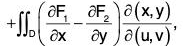 [*by Jacobian] ...(1)
[*by Jacobian] ...(1)
where D is any region in u-v plane whose image is S.
Taking the terms of F1 in the equation (1),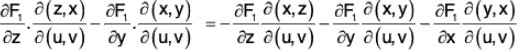 (where the additional last term = 0)
(where the additional last term = 0)
Similarly, the values of the terms F2 and F3 in (1) are respectively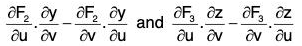
Therefore the RHS of (1)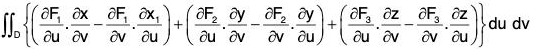
Now by Stoke’s theorem,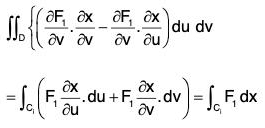
Similarly,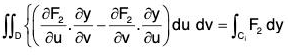
and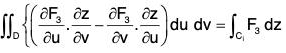
Therefore 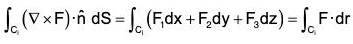
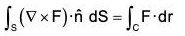
Now applying Stoke’s theorem for each subregion and adding the results,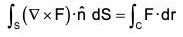
Example : Verify Stoke’s theorem for the function F = zi + xj + yk, where the curve C is the unit circle in the xy-plane bounding the hemisphere z = 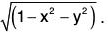
Given F = zi + xj - yk and r = xi + yj + zk
∴ F.dr = (zi + xj + yk).(idx + j dy + k dz)
or, F.dr = z dx + x dy + y dz ...(1)
The unit circle C in xy plane x2 + y2 = 1, z = 0
∴ For the curve C, z = 0 and dz = 0
∴ by (1), F.dr = x dy ...(2)
From the fig., x = cos φ, y = sin φ, where φ varies from 0 to 2π.
∴ From (2),
= 1/2[2π] = π ...(3)
From the fig, the direction cosines of the line OP are sin θ cos φ, sin θ sinφ, cos θ
Therefore= (sin θ cos φ)i + (sin θ sin φ)j + (cos θ)k,
whereis outer normal at the point P.
Now
= i + j + k
∴•(∇ x F) = [(sin θ cos φ)i + (sin θ sin φ)j + (cos θ)k]•[i + j + k]
= sin θ cos φ + sin θ sin φ + cos θ
∴where dS = sin θ dφ dθ

...(4)
Therefore from (3) and (4),
Example : Using Stoke’s theorem, evaluate : 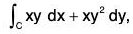 where C is the square in the xy plane with vertices respectively : (1, 0), (-1, 0), (0, 1); (0, 1)
where C is the square in the xy plane with vertices respectively : (1, 0), (-1, 0), (0, 1); (0, 1)
Writing
where dr = xi + yj
Here F = xy i + xy2 j
∴
Taking= k and dS = dx dy,
•(∇ x F) = k•(y2 -x)k = y2 - x
By Stokes’s theorem,
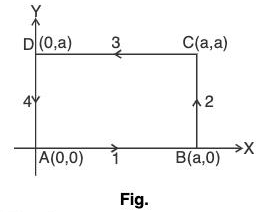
Example : Verify Stoke’s theorem for the function F = x2i + xy j integrated round the square in the plane z = 0, whose sides are along the lines x = y = 0 and x = y = 0.
In the plane z = 0, r = xi + yj
Therefore
dr = i dx + j dy
∴ F•dr = (x3i + xy j)•(i dx + j dy)
= x2 dx + xy dy
Now(a) On the line AB, y = 0, Therefore dy = 0
...(1)
(b) On the line BC, x = a, Therefore dx = 0
∴ Along the side BC of the square...(2)
(c) On the line CD, y = a, Therefore dy = 0
∴ Along the side CD of the square...(3)
(d) On the line DA, x = 0, Therefore dx = 0
∴ Along the side DA of the square...(4)
Therefore from (1), (2), (3) and (4), along the square ABCD...(5)
Check : curl F =
On square ABCD,= k, Therefore curl F
= yk•k = y
∴...(6)
From (5) and (6),
Hence the Stoke’s theorem is verified.
Example : Evaluate by Stoke’s theorem 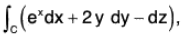 where C is the curve x2 + y2 = 4 and z = 2.
where C is the curve x2 + y2 = 4 and z = 2.
Writing
orwhere dr = i dx + j dy + k dz
Therefore taking F = exi + 2y j - k and by Stoke’s theorem...(1)
where the surface S is the boundary C of the curves, x2 + y2 = 4 and z = 2.
Here C is a circle x2 + y2 = 4 and z = 2 whose centre is D(0, 0, 2) and radius is 2 and C is also the boundary of S1, therefore= k
∴...(2)
Now
= i(0) + j(0) + k(0) = 0
From (2),
•(∇ x F) = 0
Therefore from (1), the given integral
Example : Prove by Stoke’s theorem :
(a) 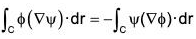
(b) 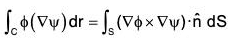
(a) By Stoke’s theorem
...(1)
Let F = ∇(φψ), therefore ∇ x f = ∇ x (∇φψ)
or, ∇ x f = 0 [∵ ∇ x (∇φψ) = 0]
Therefore from (1),...(2)
and
From (2),
or,
(b)(By Stoke's theorem) ...(1)
Let F = φ∇ψ
∴ ∇ x F = ∇ x (φ∇ψ)
= (∇φ) x ∇ψ + φ∇ x ∇ψ [∵ ∇ x fV = (∇φ) x V + φ(∇ x V)]
or, ∇ x F = ∇φ x ∇ψ [∵ ∇ x (∇ψ) = 0] ...(2)
Therefore from (1) and (2)
Green's Theorem
Statement: If φ and ψ are two continuously differentiable vector point functions such that ∇φ and ∇ψ are also continuously differentiable within V enclosed by a surface S, then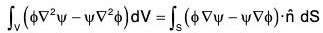
Proof. Using Gauss theorem for the vector point function φ∇ψ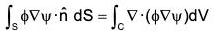 ...(1)
...(1)
But 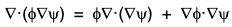
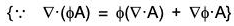
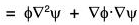 ...(2)
...(2)
From (1) and (2),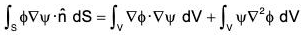 ...(3)
...(3)
Interchanging φ and ψ,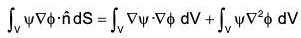 ...(4)
...(4)
Subtracting (4) and (3),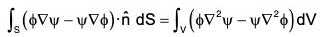 ...(5)
...(5)
which is the Green’s theorem
Another Form :
Since 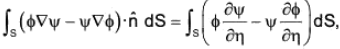
where ∂ψ/∂η is the derivative of ψ in the direction of outer normal at the point ψ.
Therefore, 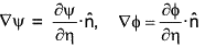
From (5), 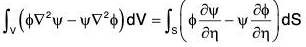
Cartesian form of Green’s Theorem :
If C is a regular closed curve in xy plane enclosing a region S, P(x, y) and Q(x, y) be two continuously differentiable functions in the region S, then :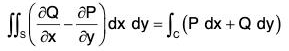
Let F = Pi + Qj, Since n = k, therefore
∴
∴...(1)
and(P dx + Q dy) ...(2)
From (1) and (2),...(3)
Cor. : When Q = x and P = -y, then
Therefore from (3),(If A is the area of the enclosed region by the curve C)
∴
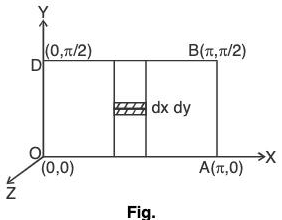
Example : Evaluate by Green’s theorem : 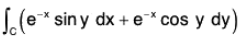 where C is the rectangle with vertices (π, 0), (0, 0), (π, π/2) and (0, π/2)
where C is the rectangle with vertices (π, 0), (0, 0), (π, π/2) and (0, π/2)
Here P = e-x sin y; Q = e-x cos y
∴ ∂P/∂Y = e-x cosy and ∂Q/∂x = -e-xcos y
∴[- cosy - cosy] = -2e-x cos y
Therefore by Green’s theorem,
Example : Use Green’s theorem to evaluate :
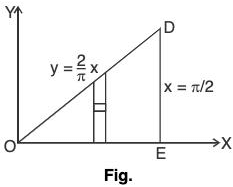
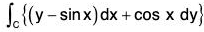 where C is the triangle enclosed by the lines y = 0, x = π/2 and y = 2x/π.
where C is the triangle enclosed by the lines y = 0, x = π/2 and y = 2x/π.
Given P = y - sin x and Q = cos x
∴
By Green’s theorem,...(1)
Substituting the values of P and Q in (1) and simplifying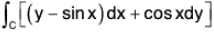
where S is the area of the triangle.
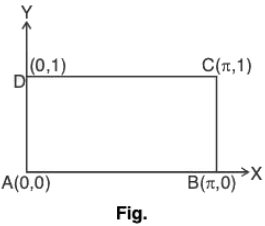
Example : Evaluate by Green’s theorem : 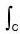 (x2 - cosh y) dx + (y + sin x )dy,
(x2 - cosh y) dx + (y + sin x )dy,
where C is the rectangle with vertices (0, 0), (π, 0), (π, 1) and (0, 1).
Taking the given points as A, B, C and D respectively, then a rectangle ABCD is obtained as given in the fig.
Here P = x2 - cosh y ⇒
and Q = y + sin x
Now by Green’s theorem,
= π cosh 1 - π = π[cosh 1 - 1]
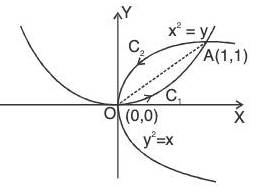
Example : Evaluate : 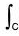 [(3x2 - 8y2)dx + (4y - 6xy)dy], where C is the region bounded by the parabolas y = √x and y = x2. Also verify Green’s theorem.
[(3x2 - 8y2)dx + (4y - 6xy)dy], where C is the region bounded by the parabolas y = √x and y = x2. Also verify Green’s theorem.
Solving the equations of the parabola y =√x and y = x2 the coordinates of the points of intersection are O(0, 0) and A(1, 1)
Here P = 3x2 - 8y2 and Q = 4y - 6xy
∴
By Green’s theorem,
= 3/2 ...(1)Verification : The line integral towards C1 (towards y = x2)
and line integral towards C2 (towards y2 = x)
Required integral = Line integral towards C1 and C2...(2)
Therefore from (1) and (2), the Green’s theorem is verified.
Example : Show that the area bounded by a simple closed curve C is given by 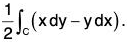 Hence find the whole area of the ellipse.
Hence find the whole area of the ellipse.
Here P = -y and Q = x
Therefore
By Green’s theorem, we know that...(1)
Substituting the values ofand Q in (1),
or...(2)
Therefore the enclosed area by the simple closed curve C = 1/2(x dy-y dx)
The given curve is an ellipse whose parametric equations are
x = a cosθ and y = b sin θ.
Therefore x = a cosθ and y = b sinθ
∴ The required area of the ellipse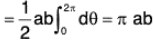
|
98 videos|41 docs|32 tests
|
FAQs on Vector Calculus - (Part - 2) - Mathematics for Competitive Exams
| 1. What is the concept of surface area and surface integrals? |  |
| 2. How is the volume integral related to surface integrals? |  |
| 3. What is Gauss's Divergence Theorem and how is it applied? |  |
| 4. How does Stoke's Theorem connect line integrals and surface integrals? |  |
| 5. What is the significance of Green's Theorem in vector calculus? |  |