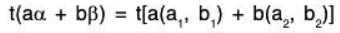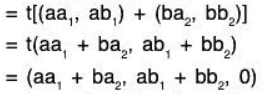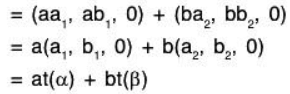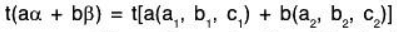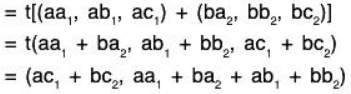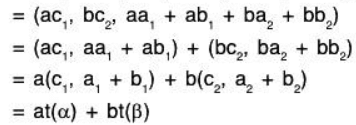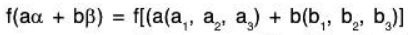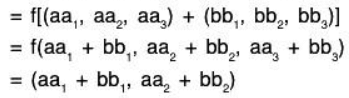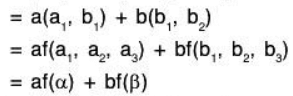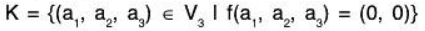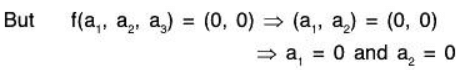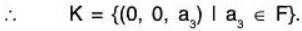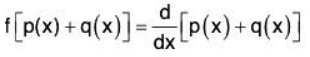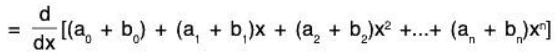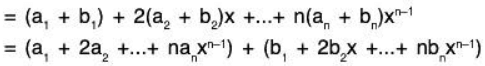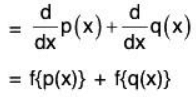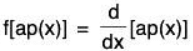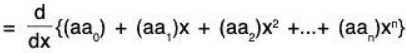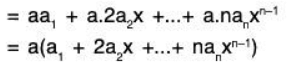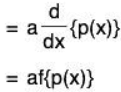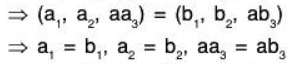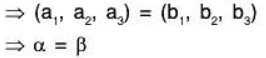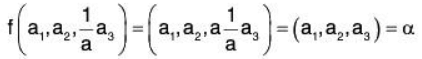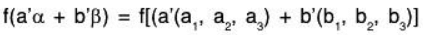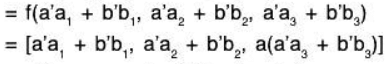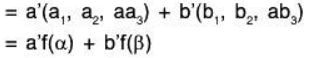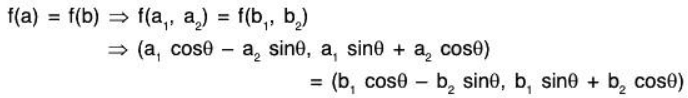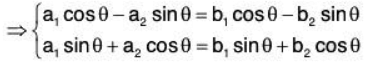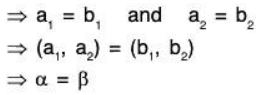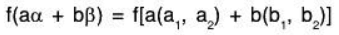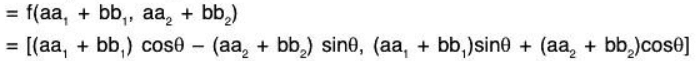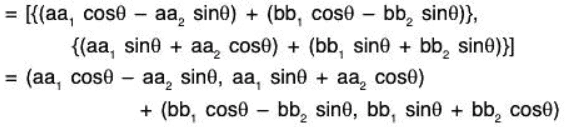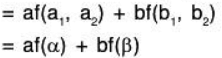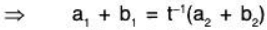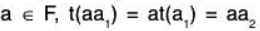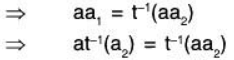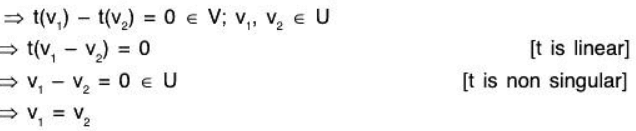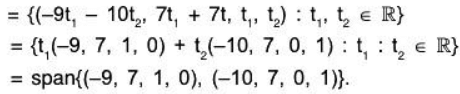Vector Space & Linear Transformation- 3 | Mathematics for Competitive Exams PDF Download
| Table of contents |

|
| Linear Transformation |

|
| Vector Space Isomorphism |

|
| Kernel and Image of a Mapping |

|
| Rank and Nullity of a Linear Mapping |

|
| Rank-Nullity Theorem |

|
Linear Transformation
We begin with a definition.
Definition: Let V and U vector spaces over the same field K. A mapping F: V → U is called a linear mapping or linear transformation if it satisfies the following two conditions:
- For any vectors v, w ∈ V, F(v + w) = F(v) + F(w).
- For any scalar k and vector v ∈ V, F(kv) = kF(v).
Namely, F: V → U is linear if it “preserves” the two basic operations of a vector space, that of vector addition and that of scalar multiplication.
Substituting k = 0 into condition (2), we obtain F(0) = 0. Thus, every linear mapping takes the zero vector into the zero vector.
Now for any scalars a, b ∈ K and any vector v, w ∈ V,
we obtain F(av + bw) = F(av) + F(bw) = aF(v) + bF(w)
More generally, for any scalars ai ∈ K and any vectors vi ∈ V, we obtain the following basic property of linear mappings: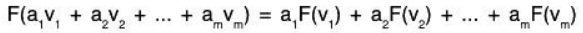
Remark: A linear mapping F: V→ U is completely characterized by the condition
F(av + bw) = aF(v) + bF(w) (*)
and so this condition is sometimes used as its definition.
Remark: The term linear transformation rather than linear mapping is frequently used for linear mappings of the form F: ℝn -> ℝm.
Some definitions
- Linear Functional: If t is a linear transformation from V(F) to F(F) i.e. t: V → F, then t is called a Linear Functional on V.
- Linear Operator: If t is a linear transformation from V to V i.e., t: V → V, then t is called a Linear Operator of V.
- Homomorphic Image: If t: V→V’ is an onto homomorphism, then V’ is called the Homomorphic image of V.
Examples of Linear Transformation:
Example: Let V(F) and V’(F) be two vector spaces. Then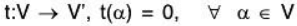
is a linear transformation from V to V'
Since for any a, b ∈ F and α, β ∈ V
t(aα + bα) = 0
= a0 + b0
= at(α) + bt(α)
This is called Zero linear mapping.
Example: Let V(F) be a vector space, then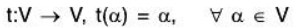
is a linear transformation from V to V (i.e. linear operation of V).
Since for any a, b ∈ F and α, β ∈ V
t(aα + bβ) = aα + bβ
= at(α) + bt(β)
Example: Let V3(F) and V2(F) be two vector spaces over the field F, then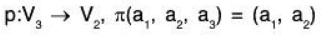
is a linear transformation from V3 to V2 since for any a, b ∈ F and (a1, a2, a3), (b1, b2, b3) ∈ V3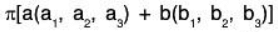
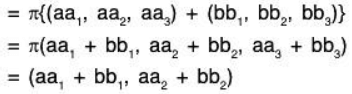
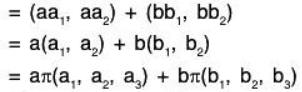
Example: t : V2(ℝ) → ℝ(ℝ), t(a1, a2) = a1 + a2 is a linear transformation from V2(ℝ) to ℝ(ℝ) i.e. a linear functional on V1
Since for any a, b ∈ R and (a1, a2); (b1, b2) ∈ V2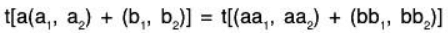
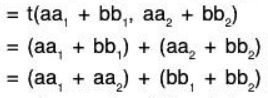
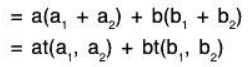
Example: t:V2(F) → F(F), t(a1, a2) = a1 is a linear functional on V2(F) since for any a, b ∈ F and (a1, a2); (b1, b2) ∈ V2.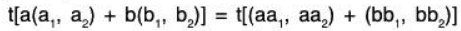
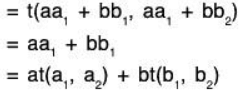
Properties of Linear mapping
Theorem: If t is a linear mapping from the vector space V(F) to V'(F), then:
(a) t(0) = 0’ where 0 and O’ are zero vectors of V and V’ respectively.
(b) t(-α) = -t(α), ∀ α ∈ V
(c) t(α - β) = t(α) - t(β), ∀ α, β ∈ V
Proof:
(a) Let α ∈ V. Since 0 is zero element in V, therefore
α + 0 = α
⇒ t(α + 0) = t(α)
⇒ t(α) + t(0) = t(α) [∵ t is a linear transformation]
⇒ t(α) + t(0) = t(α) + O' [∵ O’ is zero element in V’]
⇒ t(0) = 0’ [by cancellation law, (V’, +) being an abelian group]
(b) ∵ α ∈ V ⇒ -a e V is a additive inverse of a, therefore
α + (-α) = 0
⇒ t[α + (-α)] = t(0) = 0’ [by (a)]
⇒ t(α) + t(-α) = 0’ [∵ t is a linear transformation]
⇒ t(-α) is additive inverse of t(α) in V’
⇒ t(-α) = -t(α)
(c) t(α - β) = t[a + (-P)l
= t(α) + t(-β)] [by linear mapping]
= t(α) - t(β) [by (b)]
Kernel of a Homomorphism : Definition:
Let V(F) and V’(F) be two vector spaces and t be a homomorphism from V to V'. Then the set K of all those elements of V whose t-images are the identity O’ of V’ is called the kernel of t.
It is generally denoted by Ker t or ker t or Ker(t).
i.e. Ker t = K = {α ∈ V I t(α) = O’ ∈ V’}
Remark: The kernel of the linear transformation of t is called Null space of t and is denoted by N(t).
Theorem: The kernel of a linear transformation is a subspace.
Proof: Let V(F) and V’(F) be the two vector spaces and 0 and O’ be their zero vectors respectively. Let t be a linear transformation from V to V’ and K be the kernel of t i.e. Ker t = K = {α ∈ V I t(α) = O’ ∈ V’}
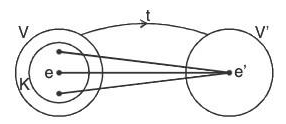 To show that K is a subspace of V:
To show that K is a subspace of V:
Therefore let α, β ∈ K, then by the definition of kernel,
t(α) = 0’ and t(β) = 0’ ...(1)
Now if a and b be any two elements of the field F, then
t(aα + bβ) = at(α) + bt(β) [∵ t is a linear transformation]
= a(0') + b(0’) [by (1)]
= 0’ + 0’
or t(aα + bβ) = 0’ [by definition]
⇒ aα + bβ ∈ K
Therefore a, b ∈ F and a, b ∈ F ⇒ aα + bβ ∈ K
∴ K is a subspace of V.
Isomorphism of Vector Spaces : Definition
Let V(F) and V'(F) be the two vector spaces, then a map
t : V → V' is called an isomorphism, if t is :
(i) one-one
(ii) onto and
(iii) a linear mapping i.e.
t(aα + bβ) = at(α) + bt(β), ∀ a, b ∈ F, V a, b ∈ V
Under these conditions, the vector spaces V and V’ are called isomorphic images any symbolically it is expressed as
V ≅ V’
Again vector space V’ is also called the isomorphic image of V.
Example 1: Prove that the mapping t : V2(ℝ) → V3(ℝ) which is defined by t(a, b) = (a, b, 0) is a linear transformation from V2 to V3.
Let α = (a, b,) and β = (a2, b2) be any two elements of V2(ℝ) and a, b ∈ ℝ, then
Therefore t is a linear transformation from V2 to V3.
Example 2: Show that the mapping t: V2(ℝ) → V3(ℝ) where t(a, b, c) = (c, a + b) is a linear mapping.
Let α = (a1, b1, c,) and β = (a2, b2, c2) be any two elements of the space V3(ℝ) and a, b ∈ R, then
Therefore t is a linear transformation from V3 to V2.
Example 3: Show that the mapping f : V3(F) → V2(F) which is defined by f(a1, a2, a3) = (a1, a2) is a homomorphism from V3 onto V2. Also find its kernel.
Let α = (a1, a2, a3) and β = (b1, b2, b3) be any two elements of the space V3(F) and a, b ∈ F, then
∴ f is a homomorphism from space V3 to V2.Onto: Let (a1, a2) ∈ V2, then corresponding to (a1, a2), there exist (a1, a2, 0) ∈ V3 for which f(a1, a2, 0) = (a1, a2)
⇒ there exist f-pre image of each element of V2 in V3
∴ f is onto homomorphism.Kernel: Let Ker f = K, then K will be the set of all the those vectors of V3 which map on the zero vector (0, 0) of V2 i.e.
Example 4: If P[x] denotes the vector space over the field of real numbers ℝ of all polynomials d in x of degree ≤ n, then prove that the mapping f : P[x] → P[x] where  is a linear transformation.
is a linear transformation.
and
be any two elements of P[x] where a0, a1, .... an; b0, b1,....., bn are all real numbers. Then
Again, for any a ∈ ℝ,
Therefore f is a linear transformation.
Example 5: Show that the mapping f: V3(ℝ) → V3(ℝ) which is defined by f(a1, a2, a3) = (a1,a2, aa3) where a ≠0 is fixed in ℝ is an isomorphism on V3(ℝ).
One-one : Let α = (a1, a2, a3) and p = (b1, b2, b3) be any two elements of the space V3(ℝ). Then
[∵ a ≠ 0]
∴ f is one-one.
Onto: For every a = (a1, a2, a3) ∈ V3(ℝ) there existfor which
∴ f is onto.
f is a linear transformation: For any a’, b’ ∈ ℝ
∴ f is a linear transformation.
Consequently, f is an isomorphism on V3(ℝ)
Example 6: Show that the mapping f : V2(ℝ) → V2(ℝ), where
(x, y) = (x cos θ - y sin θ, x sin θ + y cos θ) is an isomorphism on V2(ℝ)
One-one: Let α = (a1,a2) and β(b1,b2) be any two elements of the vector space V2(ℝ), then
∴ f is one.
Onto: Since for every (x cos θ - y sineθ, x sinθ + y cosθ) ∈ V2(ℝ) there exist (x, y) el such that f(x, y) = (x cosθ - y sinθ, x sinθ + y cosθ)
∴ f is onto.
f is a linear transformation : For any a, b ∈ ℝ
∴ f is a linear transformation.Consequently, f is an isomorphism on V2(ℝ).
Example 7: If V(F) be the vector space of all n x n matrices over the field F and M e V be a given matrix, then prove that the mapping
is a linear transformation.
Let A, B ∈ V, then
f(A + B) = (A + B)M + M(A + B)
= AM + BM + MA + MA [By distributivity of Matrices]
= (AM + MA) + (BM + MB) [By associativity for +]
= f(A) + f(B) ...(1)
Again, for any a ∈ F
f(aA) = (aA)M + M(aA)
= a(AM) + a(MA)
= a(AM + MA) By scalar multiplication of Matrices]
= af(A) ...(2)
From (1) and (2), f is a linear transformation on V(F).
Example 8: If the mapping t : V(F) → V(F’) is one-one onto linear map; then show that t-1: V’ → V will also be a linear map.
Let a1, b1 ∈ V and a2, b2 ∈ V' such that
...(1)
.... (2)
∵ t is a linear, therefore[by (1)]
[by (2)]
...(3)
and for any...(4)
From (3) and (4), it is clear than t-1 is also a linear transformation.
Example: (a) Let F ; ℝ3->:ℝ3 be the “projection” mapping into the xy-plane; that is, F is the mapping defined by F(x, y, z) = (x, y, 0). We show that F is linear. Let v = (a, b, c) and w = (a’, b’, c’). Then
and, for any scalar k,
F(kv) = K(ka, kb, kc) = (ka, kb, 0) = k(a, b, 0) = kF(v)
Thus, F is linear.
Matrices as Linear Mappings
Let A be any real m * n matrix. Recall that A determines a mapping  (where the vectors in Kn and Km are written as columns). We show FA is linear. By matrix multiplication,
(where the vectors in Kn and Km are written as columns). We show FA is linear. By matrix multiplication,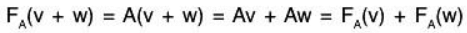
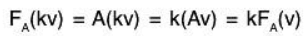
In other words, using A to represent the mapping, we have
A(v + w) = Av + Aw and A(kv) = k(Av)
Thus, the matrix mapping A is linear.
Vector Space Isomorphism
Definition: Two vector spaces V and U over K are isomorphic, written 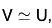 if there exists a bijective (one- to-one and onto) linear mapping F : V → U. The mapping F is then called an isomorphism between V and U.
if there exists a bijective (one- to-one and onto) linear mapping F : V → U. The mapping F is then called an isomorphism between V and U.
Consider any vector space V of dimension n and let S be any basis of V. Then the mapping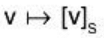
which maps each vector v ∈V into its coordinate vector [v]s, is an isomorphism between V and Kn.
Some Theorem on Space Morphism
Theorem: If W be a subspace of a vector space V(F), then the quotient space V/W, is a homomorphic image of V with kernel W.
Proof. Let a mapping f from V to V/W be defined as follows :
To prove (a) f is an onto linear transformation and (b) ker f = W
(a) If α, β ∈ V and α, β ∈ F, then
f(aα + bβ) = W + (aα + bβ)
= (W + aα) + (W + bβ)
= a(W + α) + b(W + β)
= af(α) + bf(β)
∴ f is a linear transformation.
Again for every W + α ∈ V/W, there exist α ∈ V such that
f(α) = W + α
∴ f is onto i.e. f(V) = V/W
Therefore f : V → V/W is onto homomorphism
⇒ V/W is homomorphic image of V.
(b) ker f = {α ∈ V I f(α) = W} [∵ W is zero element of V/W]
= α ∈V I W + α = W}
= {α ∈ V I α ∈ W} = W
Theorem : [Fundamental theorem on Space Homomorphism] :
If f be a linear transformation from a vector space V(F) onto V’(F), then
Proof: Let Ker f = K.
Now define a linear transformation ϕ from V/K to V’ as follows :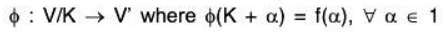 ....(1)
....(1)
ϕ is well defined: Here it will be shown that for any two elements K + α and K + β of V/K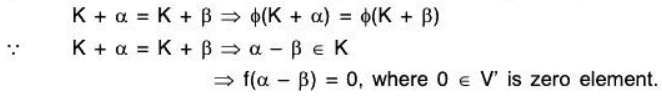
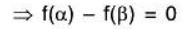 [∵ f is a linear transformation]
[∵ f is a linear transformation]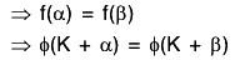
∴ ϕ is well defined.
ϕ is one-one: Let K + α, K + β ∈ V/K, then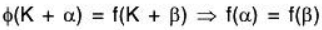 ....([by (1)])
....([by (1)])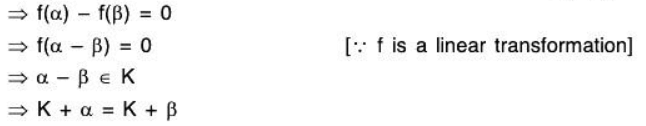
ϕ is one-one.
ϕ is onto: ∵ f is onto, therefore for every α’ ∈ V', there exist α ∈ V such that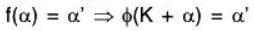 [by (1)]
[by (1)]
Therefore for α’ ∈ V there exist K + α ∈ V/K such that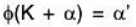
∴ ϕ is onto
ϕ is a linear transformation : For any a, b ∈ F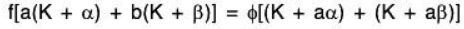

∴ ϕ is a linear transformation.
Hence ϕ is an isomorphism from V/K to V'
Consequently,
Theorem : [Isomorphism theorem for Vector Spaces]
Two FDVS V and V’ over the same field F are isomorphic iff they are of the same dimensions
i.e V ≌ V’ dim V = dimV’
Proof: Let V(F) and V’(F) be the two vector spaces and dim V = n.
Firstly, let V ≌ V', then there exist a map f from V to V' which is one-one onto linear transformation.
Let  be the basis of the space V.
be the basis of the space V.
if 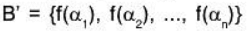
then to show that B’ is the basis of V’.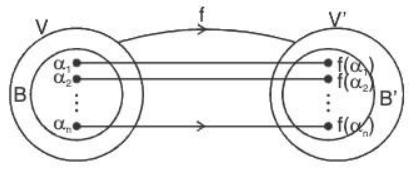
B’ is LI: Let a1, a2, ..., an ∈ F are such that
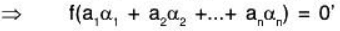 [ ∵ f is linear transformation]
[ ∵ f is linear transformation] where 0 ∈ V is zero element
where 0 ∈ V is zero element
[∵ f is one-one and f(0) = O’]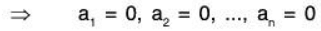
Therefore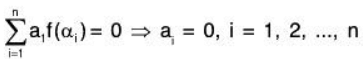
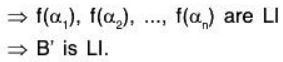
L (B’) = V’ : Let α' ∈ V ’ since f is onto,
therefore for every α' ∈ V there exist α ∈ V such that f(α) = α’
⇒ α' ∈ V' is a LC of vectors of B’
⇒ L(B’) = V’
Hence B’ is a basis of V’. Consequently dim V’ = n
∴ dim V = n = dim V’
Therefore V = V’ => dimV = dimV'
Conversely: Let dimV = dimV’. Let 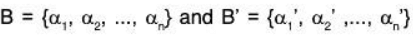 be the bases of V and V’ respectively.
be the bases of V and V’ respectively.
If α ∈ V, then there exist 
such that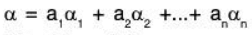
Define a map f from V to V’ as follows :
f : V → V’ such that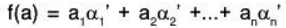
To prove that f is an isomorphism:
f is one-one: Let α, β ∈ V where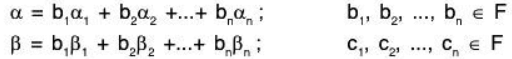
Then f(a) = f(b)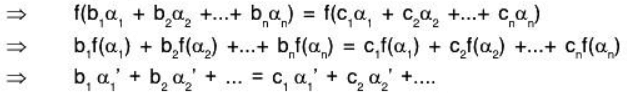
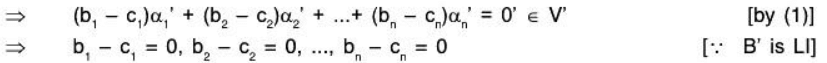

∴ f is one-one.
f is onto: Let  be any element of V’, then there exist
be any element of V’, then there exist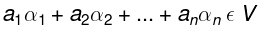 such that
such that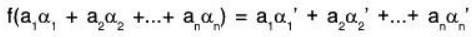
∴ f is onto.
f is a linear transformation: For any a, b ∈ F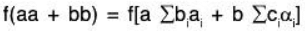
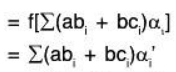
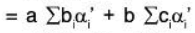 [by (1)]
[by (1)]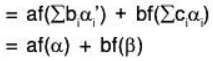
∴ f is a linear transformation.
Therefore f is an isomorphism from V to V ’ .
Consequently, V≅ V ’
Hence
Theorem: Every n-dimensional vector space V(F) is isomorphic to Vn(F) i.e.
V(F) ≅ Vn(F)
Proof: dimV(F) = n, therefore let 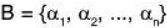 be any basis of the space Vn(F). Then every vector of V can be expressed as a LC of elements of B. Therefore for any α ∈ V there exist a1, a2, .... an ∈ F such that
be any basis of the space Vn(F). Then every vector of V can be expressed as a LC of elements of B. Therefore for any α ∈ V there exist a1, a2, .... an ∈ F such that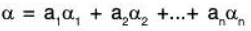
Now define a map f from V(F) to Vn(F) as follows: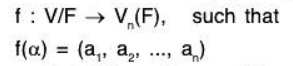
To prove that f is an isomorphism:
f is one-one: Let α, β ∈ V where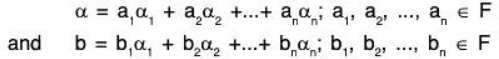
then f(α) = f(β)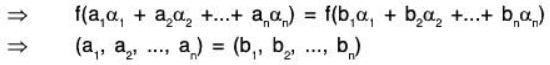
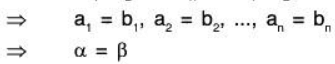
∴ f is one-one.
f is onto: Let 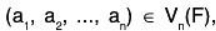 then there exist an element,
then there exist an element, 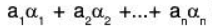 in V such that
in V such that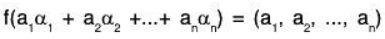
∴ f is onto.
f is a linear transformation: Let α, β ∈ V and a, b ∈ F, then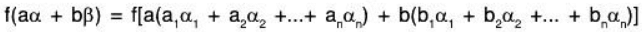
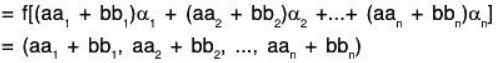
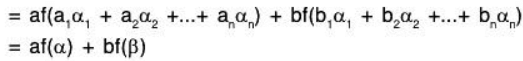
∴ f is a linear transformation.
Hence f is an isomorphism from V(F) to Vn(F).
Consequently, V(F) ≅ Vn(F).
Range space of a linear transformation: Definition:
Let V(F) and V'(F) be two vector space and t: V → V’ be a linear transformation. Then the image set of V under t is called the range space of t.
This is expressed by R(t) or lm(t).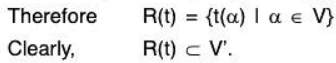
Theorem: If t is a linear transformation from a vector space V(F) to V’(F), then the range of t is a subspace of V’.
Proof: Let the range of t be R(t), then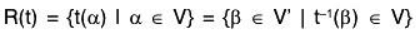
Clearly, R(t) ⊂ V’ and R(t) ≠ ϕ
Let β1, β2 ∈ R(t), then there exist α1, α2, ∈ V such that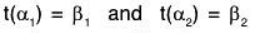
But V(F) is a vector space, therefore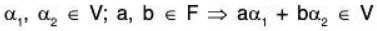
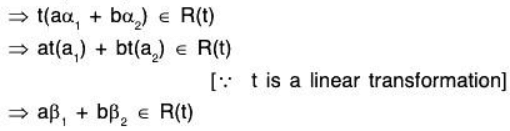
Therefore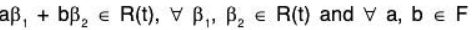
∴ R(t) is a vector subspace of V’.
Definition: A linear transformation t: U→V is called non-singular if t(u) = 0 implies u = 0.
NOTE: Moreover, U and V must be of same dimension otherwise t: U→V may not be surjective.
Example 1: A linear transformation t : U → V is an isomorphism iff it is non singular.
To show that if t is an isomorphism ⇒ t is non singular i.e. t is one-one, therefore 0 ∈ U is the only vector whose image 0 ∈ V or, only zero vector is in the zero space of t. t is non singular.
Conversely: If t is non singular ⇒ t is an isomorphism
Let t(v1) = t(v2)Hence t is one-one.
t is nonsingular and one-one, therefore this is one-one also,
∴ t is an isomorphism.
Example 2: If t : U → V is a linear transformation; then t is non singular if and only if the range of LI set by t in U is LI set in V.
First let t be nonsingular i.e. only zero vector is in the empty space of t.
Let B = {v1, v2, ....., vn} be a LI subset of U, then its image set under t is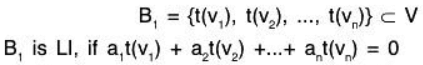
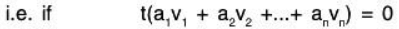 [t is linear]
[t is linear] [t is nonsingular]
[t is nonsingular]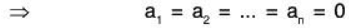 [B is LI]
[B is LI]
Hence the image B, of B under t is LI.
Conversely: Let t-image of any LI set of U be LI in V.
Consider a nonzero vector v of U, then the set
S = {v} is a LI set in V.
Now t-image S, of S contains only an element t(v)
[Note]
S, = {t(v)},
S, is LI in V, therefore for v ≠ 0, t(v) ≠ 0,
because the set containing zero element alone is LI.
Consequently, the null space of t is null subspace, i.e. t is nonsingular.
Kernel and Image of a Mapping
We begin by defining two concepts.
Definition Let F : V → U be a linear mapping. The kernel of F, written Ker F, is the set of elements in V that map into zero vector 0 in U; that is,
Ker F = {v ∈ V : F(v) = 0}
The image (or range) of F, written Im F, is the set of image points in U; that is,
Im F = (u ∈ U : there exists v ∈ V for which F(v) = u}
Theorem: Let F : V → U be a linear mapping. Then the kernel of F is a subspace of V and the image of F is a subspace of U.
Now suppose that v1, v2, ..., vm span a vector space V and that F : V → U is linear. We show that F(v1), F(v2), ..., F(vm) span Im F. Let u ∈ Im F. Then there exists v ∈ V such that F(v) = u. Because the vi’s span V and v ∈ V, there exist scalars a1, a2, ..., am for which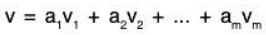
Therefore,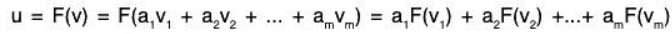
Thus, the vectors F(v1), F(v2),....., F(vm) span Im F.
Proposition: Supposev1, v2, ..., vm span a vector space V, and suppose F : V → U is linear. Then F(v1), F(v2),....., F(vm) space Im F.
Example: (a) Let F : ℝ3 → ℝ3 be the projection of a vector v into the xy-plane, i.e.
F(x, y, z) = (x, y, 0)
Clearly the image of F is the entire xy-plane—that is, points of the form (x, y, 0). Moreover, the kernel of F is the z-axis—that is, points of the form (0, 0, c). That is,
Im F = {(a, b, c) : c = 0} = xy-plane and Ker F = {(a, b, c) : a = 0, b = 0} = z-axis
Kernel and Image of Matrix Mappings
Consider, say, a 3 * 4 matrix A and the usual basis {e1, e2, e3, e4} of K4 (written as columns):
Recall that A may be viewed as a linear mapping A : K4 → K3, where the vectors in K4 and K3 are viewed as column vectors. Now the usual basis vectors span K4 so their images Ae1, Ae2, Ae3, Ae4, span the image of A. But the vectors Ae1, Ae2, Ae3, Ae4 are precisely the columns of A: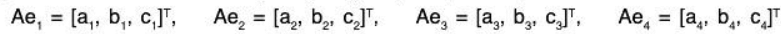
Thus, the image of A is precisely the column space of A.
On the other hand, the kernel of A consists of all vectors v for which Av = 0. This means that the kernel of A is the solution space of the homogeneous system AX = 0, called the null space of A.
Proposition: Let A be any m * n matrix over a field K viewed as a linear map A : Kn → Km. Then
Ker A = nullsp(A) and Im A = colsp(A)
Here colsp(A) denotes the column space of A, and nullsp(A) denotes the null space of A.
Rank and Nullity of a Linear Mapping
Let F : V → U be a linear mapping. The rank of F is defined to be the dimension of its image, and the nullity of F is defined to be the dimension of its kernel; namely,
rank(F) = dim(lm F) and nullity(F) = dim(Ker F)
Theorem: Let V be of finite dimension, and let F : V → U be linear. Then
dim V = dim(Ker F) + dim(lm F) = nullity(F) + rank(F)
Matrix Representation of a Linear Operator
Let T be a linear operator (transformation) from a vector space V into itself, and suppose S = {u1, u2, ...., un} is a basis of V. Now T(u1), T(u2),..., T(un) are vectors in V, and so each is a linear combination of the vectors in the basis S; say,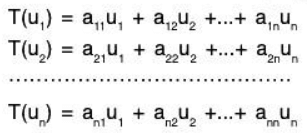
Definition
The transpose of the above matrix of coefficients, denoted by ms(T) or [T]s, is called the matrix representation of T relative to the basis S, or simply the matrix of T in the basis S.
Example: Let F: ℝ2 → ℝ2 be the linear operator defined by F(x, y) = (2x + 3y, 4x - 5y).
(a) Find the matrix representation of F relative to the basis S = {u1, u2} = {(1, 2), (2, 5)}.
- First find F(u1), and then write it as a linear combination of the basis vectors u1 and u2. (For notational convenience, we use column vectors.) We have
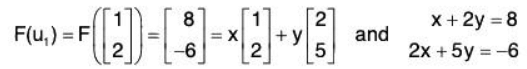
Solve the system to obtain x = 52, y = -22. Hence, F(ut) = 52u1 - 22u2. - Next find F(u2), and then write it as a linear combination of u1 and u2:
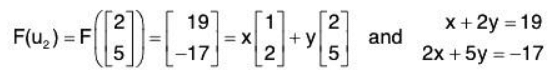 Solve the system to get x = 129, y = -55. Thus F(u2) = 129u1 - 55u2.
Solve the system to get x = 129, y = -55. Thus F(u2) = 129u1 - 55u2.
Now write the coordinates of F(u,) and F(u2) as columns to obtain the matrix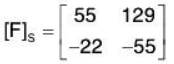
Example: Let F : ℝ4 → ℝ3 be the linear mapping defined by
F(x, y, z, t) = (x - y + z + t, 2x - 2y + 3z + 4t, 3x - 3y + 4z + 5t)
(a) Find a basis of the dimension of the image of F.
Find first the image of the usual basis vectors of R4.
F(1, 0, 0, 0) = (1. 2, 3), F(0, 0, 1, 0) = (1, 3, 4)
F(0, 1, 0, 0) = (-1, -2, -3), F(0, 0, 0, 1) = (1, 4, 5)
By Proposition the image vectors span Im F. Hence, form the matrix M whose rows are these image vectors and row reduce to echelon form: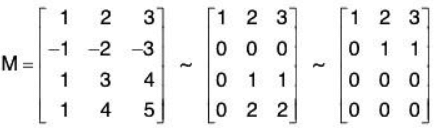
Thus, (1, 2, 3) and (0, 1, 1) form a basis of Im F. Hence, dim(lm F) = 2 and rank(F) = 2.
Change of Basis
Let V be an n-dimensional vector space over a field K. We have shown that once we have selected a basis S of V, every vector v ∈ V can be represented by means of an n-tuple [v]s in Kn, and every linear operator T in A(V) can be represented by an n * n matrix over K.
Definition
Let S = {u1, u2, ...., un} be a basis of a vector space V, and let S’ = {v1, v2, ..., vn} be another basis. (For reference, we will call S the “old” basis and S’ the “new" basis.) Because S is a basis, each vector in the “new” basis S' can be written uniquely as a linear combination of the vectors in S; say,
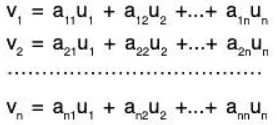
Let P be transpose of the above matrix of coefficients; that is, let P = [pij], where pij = aji, Then P is called the change-of-basis matrix (or transition matrix) from the “old” basis S to the “new” basis S’.
The following remarks are in order.
Remark: The above change-of-basis matrix P may also be viewed as the matrix whose columns are, respectively, the coordinate column vectors of the “new” basis vectors v. relative to the “old" basis S; namely,
P = [[V1]s, [V2]s,......, [Vn]S]
Remark: Analogously, there is a change-of-basis matrix Q from the “new” basis S' to the “old” basis S. Similarly, Q may be viewed as the matrix whose columns are, respectively, the coordinate column vectors of the “old” basis vectors u. relative to the “new” basis S’; namely,
Q = [[u1]s, [u2]s,......, [un]S]
Remark : Because the vectors v1, v2, ..., vn in the new basis S’ are linearly independent, the matrix P is invertible. Similarly, Q is invertible. In fact, we have the following proposition.
Proposition: Let P and Q be the above change-of-basis matrices. Then Q = P-1.
Now suppose S = {u1, u2,.....,un} is a basis of a vector space V, and suppose P = [pij] is any nonsingular matrix. Then the n vectors
corresponding to the columns of P, are linearly independent. Thus they form another basis S’ of V. Moreover, P will be the change-of-basis matrix from S to the new basis S’.
Example: Consider the following two bases of ℝ2: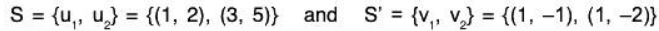
(a) Find the change-of-basis matrix P from S to the “new” basis S”. Write each of the new basis vectors of S’ as a linear combination of the original basis vectors u, and u2 of S. We have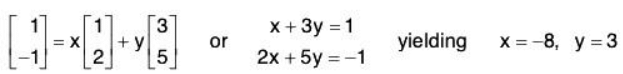
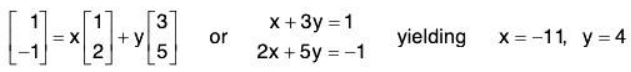
Thus
Note that the coordinates of v1 and v2 are the columns, not rows, of the change-of-basis matrix P.
Rank-Nullity Theorem
If t is a linear transformation defined from a vector space V(F) to V'(F) where V(F) is a finite dimensional, then :
Rank (t) + Nullity (t) = Dim V.
Proof. Let V(F) be a n-dimensional vector space and R and K be their range and kernel respectively.
Define a mapping ϕ from R to V/K as follows:
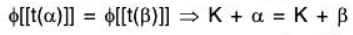
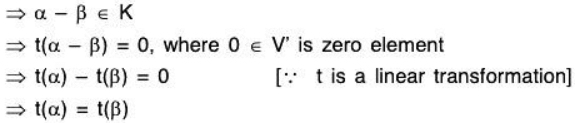
∴ ϕ is one-one.
ϕ is onto : Let K + α ∈ V/E, then there exist t(α) ∈ ℝ such that
ϕ[t(α)] = K + α
Therefore preimage of each element of V/K exist in ℝ.
∴ ϕ is onto.
ϕ is a linear transformation: For any a, b ∈ F and t(α), t(β) ∈ ℝ f[at(α) + bt(β)] = ϕ[t(aα + bβ)] [∵ t is a linear transformation]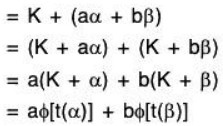
∴ ϕ is a linear transformation.
Hence ϕ is an isomorphism from R to V/K.
⇒ ℝ ≅ V/K
⇒ dim ℝ = dim(V/K)
⇒ dim ℝ = dim V - dim K
⇒ dim ℝ + dim K = dim V
⇒ Rank(t) + Nullity(t) = dimV.
Example 1: If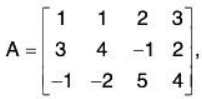
find a basis for nullspace (A) and verify Theorem.
We must find all solutions to Ax = 0. Reducing the augmented matrix of this system yields
Consequently, there are two free variables, x3 = t, and x4 = t2, so that
x2 = 7t, + 7t2, x1 = —9t1 - 10t2.Hence,
nullspace (A)
Since the two vectors in this spanning set are not proportional, they are linearly independent. Consequently, a basis for nullspace(A) is {(-9, 7, 1, 0), (-10, 7, 0, 1)}, so that nullity(A) = 2. In this problem, A is 3 * 4 matrix, and so, in the Rank-Nullity Theorem, n = 4. Further, from the foregoing row- echelon form of the augmented matrix of the system Ax = 0, we see that rank(A) = 2. Hence, rank(A) + nullity(A) = 2 + 2 = 4 = Dim(A) and the Rank-Nullity Theorem is verified.
Example: Find rank (A) and nullity (A) for A
- rank (A). It is enough to put A in row-echelon form and count the number of leading ones.
The reader will verify that a row-echelon form of A = is . There are three leading ones, therefore rank (A) = 3.
. There are three leading ones, therefore rank (A) = 3. - nullity (A). For this, we need to find a basis for the solution set of Ax = 0. Its reduced row-echelon form is:
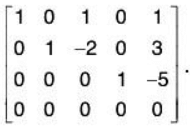 Then corresponding system is
Then corresponding system is 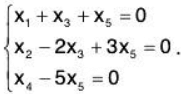 The leading variables are x1, x2, and x4. Hence, the free variables are X3 and x5. We can write the solution in parametric form as follows:
The leading variables are x1, x2, and x4. Hence, the free variables are X3 and x5. We can write the solution in parametric form as follows: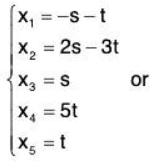

Thus, nullity (A) = 2 .
Example : Find the rank and nullity of 
Note this matrix has 5 columns. The row-echelon form is 
We see that rank(A) = 2 (2 leading 1’s). Therefore nullity (A) = 5 - 2 = 3.
|
98 videos|34 docs|32 tests
|
FAQs on Vector Space & Linear Transformation- 3 - Mathematics for Competitive Exams
| 1. What is a linear transformation? |  |
| 2. What is a vector space isomorphism? |  |
| 3. What is the kernel and image of a mapping? |  |
| 4. What is the rank and nullity of a linear mapping? |  |
| 5. What is the Rank-Nullity Theorem in vector space and linear transformation? |  |