Vectors and Newton's law of Motion | Basic Physics for IIT JAM PDF Download

Different physical quantities can be classified into the following two categories:

What are Scalars?

Scalar quantity is defined as the physical quantity that has magnitude but no direction.

• It can be represented by a number only. Example: Mass = 4 kg
• The magnitude of mass = 4, Unit of mass = kg
• Scalar quantities can be added, subtracted, and multiplied by simple lawsofalgebra.
• Examples of Scalar Quantities includemass, speed, distance, time, area, volume, density & temperature.

What are Vectors?

A vector quantity is defined as the physical quantity that has both direction as well as magnitude and follows law of vector addition.

Vectors

For example, Speed = 4 m/s (is a scalar), Velocity = 4 m/s toward north (is a vector).

• The magnitude of a vector is the absolute value of a vector and is indicated by |A|.
• Example of Vector quantity: Displacement, velocity, acceleration, force, etc.

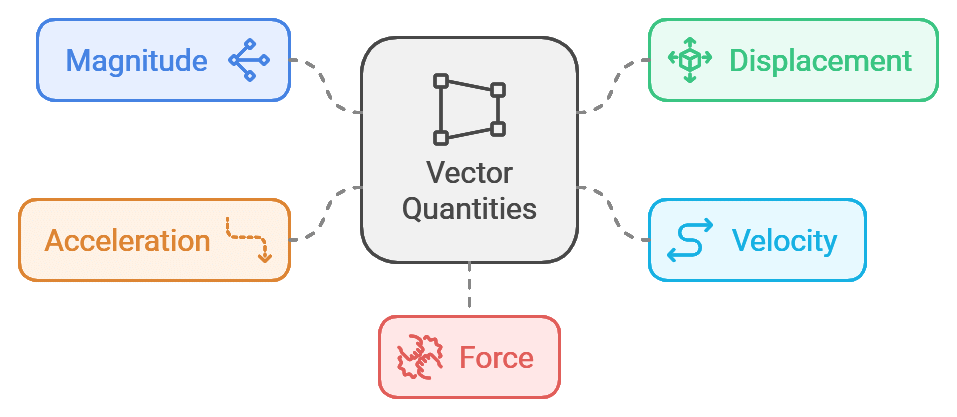
Difference between scalar and vector quantities is mentioned in table below:

Vector Operations

(i) Addition of two vectors

• Place the tail of 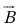at the head of 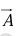; the sum 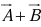, is the vector from the tail of 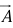to the head of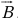
• Addition is commutative:
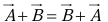
• Addition is associative:
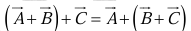
• To subtract a vector, add its opposite

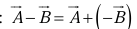
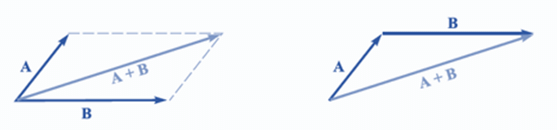
(ii) Multiplication by scalar

Multiplication of a vector by a positive scalar a, multiplies the magnitude but leaves the direction unchanged. (If a is negative, the direction is reversed.)

Scalar multiplication is distributive: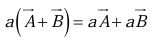

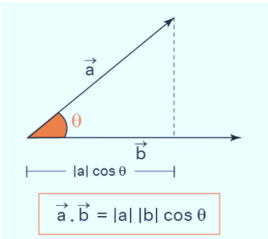
(iii) Dot product of two vectors

The scalar product of two vectors is equal to the product of their magnitudes and the cosine of the smaller angle between them. 

It is denoted by.(dot). The scalar or dot product of two vectors is a scalar.

A . B = AB cos θ

Properties of Scalar Product:

• Scalar product is commutative, i.e.,
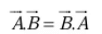
• Scalar product is distributive, i.e.,
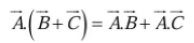
• Scalar product of two perpendicular vectors is zero.
  A . B = A B cos 90° = 0
• Scalar product of two parallel vectors is equal to the product of their magnitudes, i.e., A . B = AB cos 0° = AB
• Scalar product of a vector with itself is equal to the square of its magnitude, i.e.,
  A . A = A A cos 0° = A²
• Scalar product of orthogonal unit vectors is zero and Scalar product in cartesian coordinates is given by A_xB_x + A_yB_y + A_zB_z .

Law of Cosines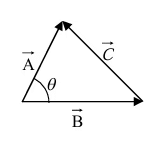

Let 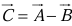and then calculate dot product of 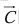with itself.

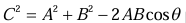
(iv) Cross product of two vectors

The vector product of two vectors is equal to the product of their magnitudes and the sine of the smaller angle between them. It is denoted by X (cross).

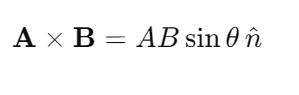
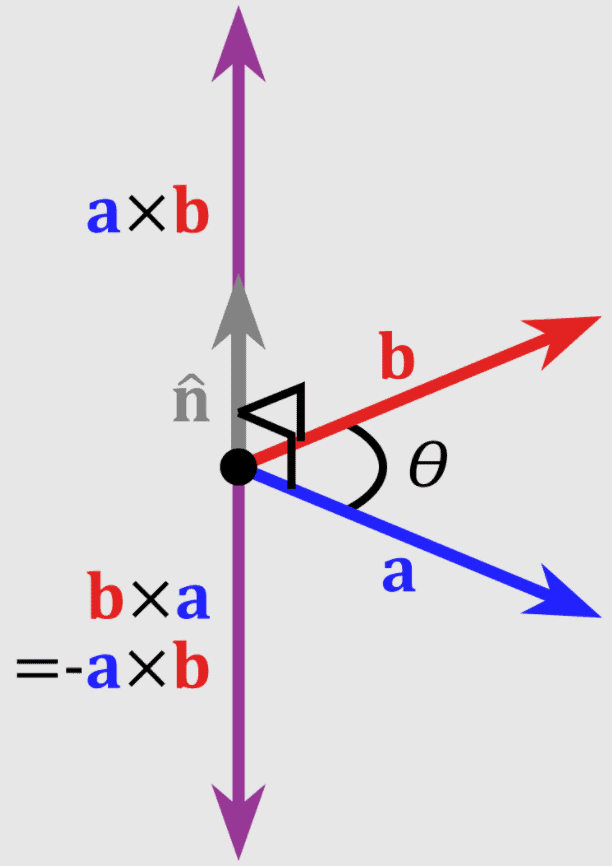Vector Cross Product

• The direction of unit vector n can be obtained from right hand thumb rule.
• If fingers of right hand are curled from A to B through smaller angle between them, then thumb will represent the direction of vector (A X B).
• The vector or cross product of two vectors is also a vector.

Properties of Vector Product:

• Vector product is not commutative, i.e.,
  A X B ≠ B X A  [ therefore, (A X B) = - (B X A)]
• Vector product is distributive, i.e.,
  A X (B + C) = A X B + A X C
• Vector product of two parallel vectors is zero, i.e.,
  A X B = A B sin 0° = 0
• Vector product of any vector with itself is zero.
  A X A = A A sin 0° = 0
• On moving in a clockwise direction and taking the cross product of any two pair of the unit vectors we get the third one and in an anticlockwise direction, we get the negative resultant.

The following results can be established:

Direction of Vector Cross Product

• When C = A X B, the direction of C is at right angles to the plane containing the vectors A and B. The direction is determined by the right hand screw rule, and right hand thumb rule.
• Right Hand Thumb Rule: Curl the fingers of your right hand from A to B. Then, the direction of the erect thumb will point in the direction of A X B.
  
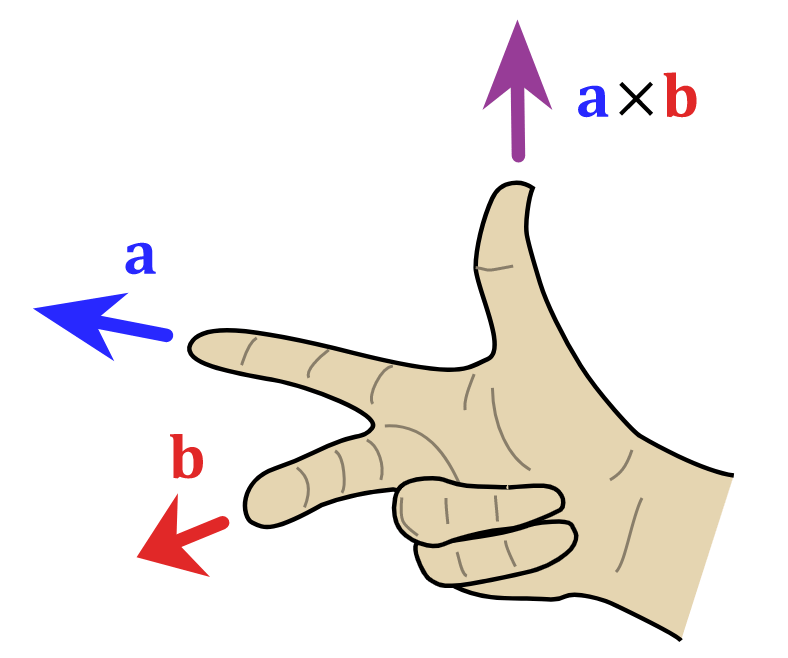  Right Hand Thumb Rule
  
  
• Right Hand Screw Rule: It is also known as Maxwell's Screw Rule,  a simple and visual way to determine the direction of a magnetic field or angular motion in relation to a current or rotation.
  Explanation:
• Imagine holding a screw and turning it with a screwdriver.
• The direction in which you turn the screw (clockwise or counterclockwise) is the direction of rotation.
• The direction in which the screw moves (up or down along the axis) corresponds to the direction of the currentor the magnetic field.

Component Form: Vector Algebra

Let 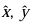 and 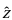be unit vectors parallel to the x, y and z axis, respectively. An arbitrary vector 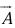can be expanded in terms of these basis vectors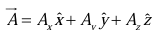

The numbers 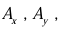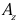and are called component of 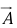; geometrically, they are the projections of 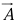along the three coordinate axes.

Rule 1:To add vectors, add like components.  

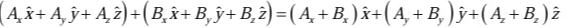
Rule 2: To multiply by a scalar, multiply each component.      

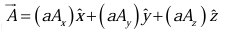Because are mutually perpendicular unit vectors,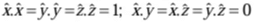  

Accordingly,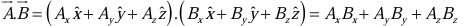

Rule 3: To calculate the dot product, multiply like components, and add.

In particular,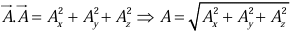  

Similarly,

Rule 4: To calculate the cross product, form the determinant whose first row is whose second row is (in component form), and whose third row is .

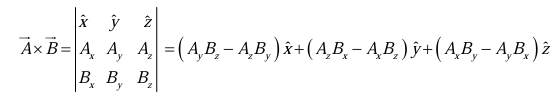
Example 1: Find the angle between the face diagonals of a cube.

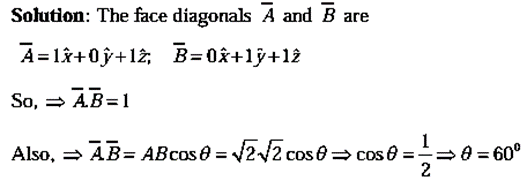
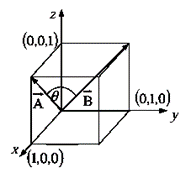
What are Triple Products?

Since the cross product of two vectors is itself a vector, it can be dotted or crossed with a third vector to form a triple product.

(i) Scalar triple product: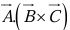

Geometrically 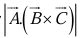is the volume of the parallelepiped generated by 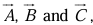since is the area of the base, and 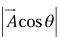is the  altitude.

Evidently,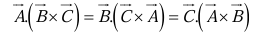

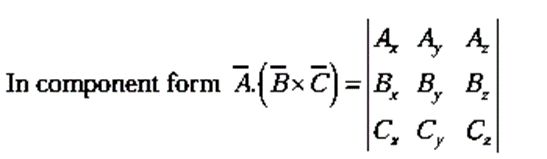
Note that the dot and cross can be interchanged:

(ii) Vector triple product: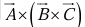

The vector triple product can be simplified by the so-called BAC-CAB rule: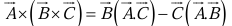

Newton's Law of Motion

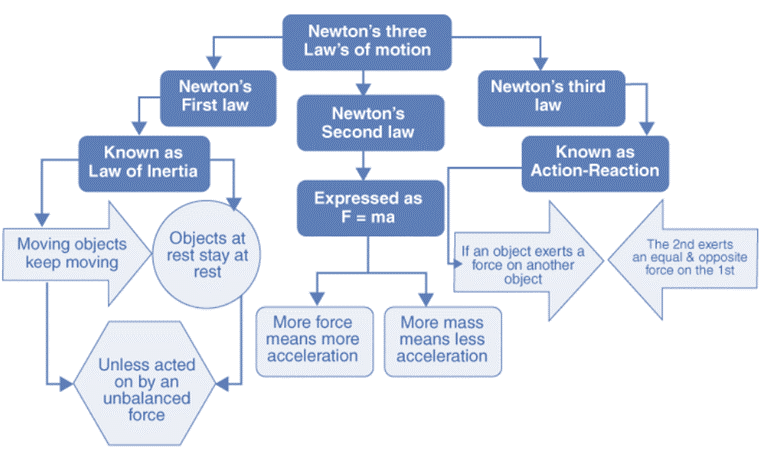
Newton's Laws of Motion are three fundamental principles that underpin classical mechanics. These laws explain how a body interacts with the forces acting upon it and how it moves as a result of those forces.

1. First Law (Law of Inertia)

The first law states that if the net force acting on an object (the total of all forces) is zero, the object's momentum remains constant in both size and direction.

• Inertia is a basic property of matter that resists any change in its state of motion. It is generally measured by mass; the larger the mass, the greater the inertia.
• An inertial frame is a coordinate system with a clock that moves at a constant speed. Within such a frame, if no external force acts on an object, it will either stay at rest or continue to move at a constant velocity.
• Mathematically, the first law can be represented as:

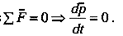
2. Second Law

The second law states that the net force on an object is equal to the rate of change (that is, the derivative) of its linear momentum in an inertial reference frame i.e.

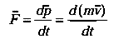
If the mass is constant then the vector sum of the external forces 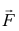on an object is equal to the mass m of that object multiplied by the acceleration vector 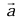of the object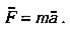

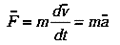
One can visualize Newton’s second law as cause and effect phenomenon where external force is equivalent to cause and resulting acceleration is its effect which is measured by a force. 

In the case when the velocity is very high (close to velocity of light) Newton’s law should be modified according to special theory of relativity.

3. Third Law   

The third law states that "To every action there is an equal and opposite reaction".

The action and reaction acts on two different bodies.

Consider two bodies body one exerts a force 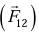on second body and the second body simultaneously exerts a force 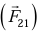equal in magnitude and opposite in direction on the first body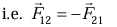

To summarise, here is the flowchart:

Some interesting FAQs are as follows:-

Q1. How do you determine if two vectors are coplanar?

Ans. Three vectors $<span\; style="background-color:\; transparent;\; word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;">and\; <img\; src="https://cn.edurev.in/cdn\_assets/v324/assets/img/ph.png"\; style="display:\; inline-block;\; margin-right:\; 5px;\; margin-left:\; 5px;\; text-align:\; center;\; max-width:\; calc(100\%\; -\; 10px);\; width:\; 22px;"\; fr-original-class="fr-draggable"\; alt="Vectors\; and\; Newton`s\; law\; of\; Motion\; |\; Basic\; Physics\; for\; IIT\; JAM"\; data-src="https://cn.edurev.in/ApplicationImages/Temp/24733558\_7e68e72f-7dbc-4b7f-a73b-9f80dacf8034\_lg.png"></span>$$\mathrm{<br\; style="word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;">}<span\; style="background-color:\; transparent;\; word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;">are\; coplanar\; if\; their\; scalar\; triple\; product\; is\; zero:</span>$

$Q2. Why are vectors so important in physics and mathematics?Ans. Vectors are fundamental in understanding and solving problems involving quantities with both magnitude and direction. They describe forces, velocities, accelerations, and more, making them essential for mechanics, electromagnetism, fluid dynamics, and even quantum mechanics.$

Q3.  How are vectors applied in mechanics?
Ans. Vectors are fundamental in mechanics for:

• Representing forces, velocities, and accelerations.
• Solving equilibrium problems in statics.
• Analyzing motion in dynamics.

Q4. What does it mean for two vectors to be linearly dependent?
Ans. Two vectors $\mathrm{<br\; style="word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;">}<span\; style="background-color:\; transparent;\; word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;">and\; <img\; src="https://cn.edurev.in/cdn\_assets/v324/assets/img/ph.png"\; style="display:\; inline-block;\; margin-right:\; 5px;\; margin-left:\; 5px;\; text-align:\; center;\; width:\; 23px;\; max-width:\; calc(100\%\; -\; 10px);"\; fr-original-class="fr-draggable"\; alt="Vectors\; and\; Newton`s\; law\; of\; Motion\; |\; Basic\; Physics\; for\; IIT\; JAM"\; data-src="https://cn.edurev.in/ApplicationImages/Temp/24733558\_89004fd5-aff1-4e53-9ace-2dc72125fcc8\_lg.png"></span>$$\mathrm{<br\; style="word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;">}<span\; style="background-color:\; transparent;\; word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;"> are\; linearly\; dependent\; if\; one\; is\; a\; scalar\; multiple\; of\; the\; other:</span>$

This means they lie along the same line or are parallel.

Q5.  What are eigenvectors, and why are they important in vector spaces?
Ans. Eigenvectors are special vectors that do not change direction under a linear transformation. They are critical in understanding physical systems, such as vibrations and quantum mechanics:

where λ is the eigenvalue.

Q6. Who discovered the three laws of motion?
Ans. Sir Isaac Newton discovered the three laws of motion.

Q7. Can Newton’s laws explain rocket launches?
Ans. Yes, Newton’s laws, especially the third law, explain rocket launches. The exhaust gases are expelled downward with great force (action), and the rocket moves upward with an equal and opposite force (reaction).

Q8.  How do Newton’s laws differ from Einstein’s theories of relativity?
Ans. Newton’s laws apply to everyday speeds and objects, where effects of relativity are negligible. Einstein’s theories of relativity apply when objects approach the speed of light or are in strong gravitational fields.

Q9: How do Newton’s laws apply to sports?
Ans. Newton’s laws are crucial in sports:

1st Law: A stationary basketball remains still until a player applies force to throw it.

2nd Law: The harder a player kicks a ball, the faster it accelerates.

3rd Law: When a swimmer pushes water backward with their hands, they move forward.

Q10. What is the role of vectors in electromagnetism?
Ans. In electromagnetism, vectors represent electric and magnetic fields. Vector operations like divergence, curl, and gradient are used to describe Maxwell’s equations and field interactions.