Venn Diagram | Mathematics for ACT PDF Download
Introduction
A Venn diagram is used to visually represent the differences and the similarities between two concepts. Venn diagrams are also called logic or set diagrams and are widely used in set theory, logic, mathematics, businesses, teaching, computer science, and statistics.
What is a Venn Diagram?
A Venn diagram is a diagram that helps us visualize the logical relationship between sets and their elements and helps us solve examples based on these sets. A Venn diagram typically uses intersecting and non-intersecting circles (although other closed figures like squares may be used) to denote the relationship between sets.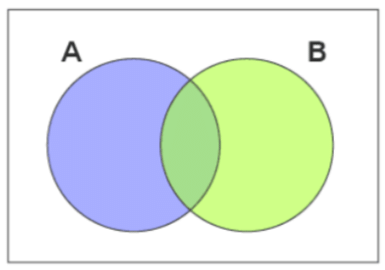
Venn Diagram Example
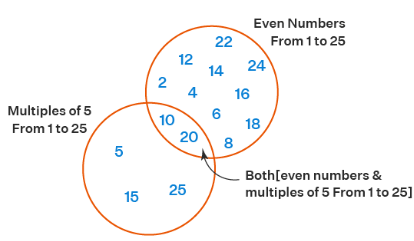
Let us observe a Venn diagram example. Here is the Venn diagram that shows the correlation between the following set of numbers.
- One set contains even numbers from 1 to 25 and the other set contains the numbers in the 5x table from 1 to 25.
- The intersecting part shows that 10 and 20 are both even numbers and also multiples of 5 between 1 to 25.
Terms Related to Venn Diagram
Let us understand the following terms and concepts related to Venn Diagram, to understand it better.
Universal Set
Whenever we use a set, it is easier to first consider a larger set called a universal set that contains all of the elements in all of the sets that are being considered. Whenever we draw a Venn diagram:
- A large rectangle is used to represent the universal set and it is usually denoted by the symbol E or sometimes U.
- All the other sets are represented by circles or closed figures within this larger rectangle.
- Every set is the subset of the universal set U.
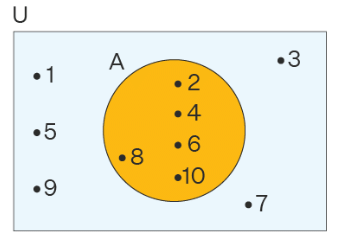
Consider the above-given image:
- U is the universal set with all the numbers 1-10, enclosed within the rectangle.
- A is the set of even numbers 1-10, which is the subset of the universal set U and it is placed inside the rectangle.
- All the numbers between 1-10, that are not even, will be placed outside the circle and within the rectangle as shown above.
Subset
Venn diagrams are used to show subsets. A subset is actually a set that is contained within another set. Let us consider the examples of two sets A and B in the below-given figure. Here, A is a subset of B. Circle A is contained entirely within circle B. Also, all the elements of A are elements of set B.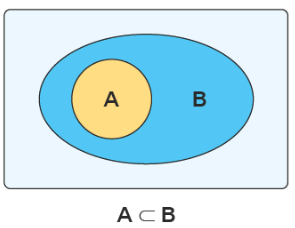
This relationship is symbolically represented as A ⊆ B. It is read as A is a subset of B or A subset B. Every set is a subset of itself. i.e. A ⊆ A. Here is another example of subsets:
- N = set of natural numbers
- I = set of integers
- Here N ⊂ I, because all-natural numbers are integers.
Venn Diagram Symbols
There are more than 30 Venn diagram symbols. We will learn about the three most commonly used symbols in this section. They are listed below as:
Let us understand the concept and the usage of the three basic Venn diagram symbols using the image given below.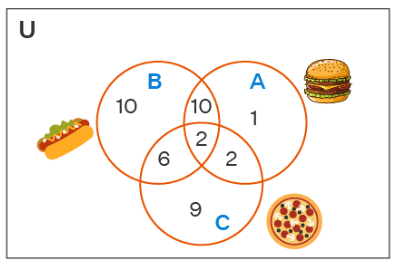
Venn Diagram for Sets Operations
In set theory, we can perform certain operations on given sets. These operations are as follows,
- Union of Sets Venn Diagram
The union of two sets A and B can be given by: A ∪ B = {x | x ∈ A or x ∈ B}. This operation on the elements of set A and B can be represented using a Venn diagram with two circles. The total region of both the circles combined denotes the union of sets A and B. - Intersection of Set Venn Diagram
The intersection of sets, A and B is given by: A ∩ B = {x : x ∈ A and x ∈ B}. This operation on set A and B can be represented using a Venn diagram with two intersecting circles. The region common to both the circles denotes the intersection of set A and Set B. - Complement of Set Venn Diagram
The complement of any set A can be given as A'. This represents elements that are not present in set A and can be represented using a Venn diagram with a circle. The region covered in the universal set, excluding the region covered by set A, gives the complement of A. - Difference of Set Venn Diagram
The difference of sets can be given as, A - B. It is also referred to as a ‘relative complement’. This operation on sets can be represented using a Venn diagram with two circles. The region covered by set A, excluding the region that is common to set B, gives the difference of sets A and B.
We can observe the above-explained operations on sets using the figures given below,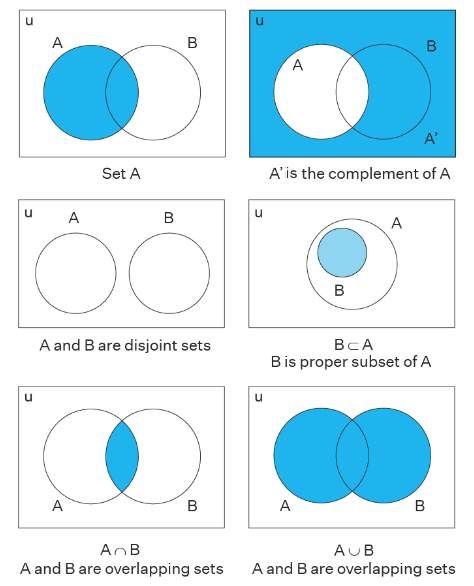
Venn Diagram for Three Sets
Three sets Venn diagram is made up of three overlapping circles and these three circles show how the elements of the three sets are related. When a Venn diagram is made of three sets, it is also called a 3-circle Venn diagram. In a Venn diagram, when all these three circles overlap, the overlapping parts contain elements that are either common to any two circles or they are common to all the three circles. Let us consider the below given example: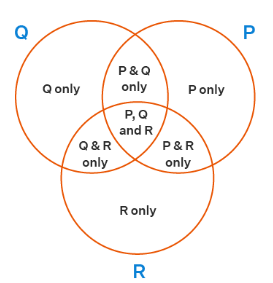
Here are some important observations from the above image:
- Elements in P and Q = elements in P and Q only plus elements in P, Q, and R.
- Elements in Q and R = elements in Q and R only plus elements in P, Q, and R.
- Elements in P and R = elements in P and R only plus elements in P, Q, and R.
How to Draw a Venn Diagram?
Venn diagrams can be drawn with unlimited circles. Since more than three becomes very complicated, we will usually consider only two or three circles in a Venn diagram. Here are the 4 easy steps to draw a Venn diagram:
- Step 1: Categorize all the items into sets.
- Step 2: Draw a rectangle and label it as per the correlation between the sets.
- Step 3: Draw the circles according to the number of categories you have.
- Step 4: Place all the items in the relevant circles.
Example: Let us draw a Venn diagram to show categories of outdoor and indoor for the following pets: Parrots, Hamsters, Cats, Rabbits, Fish, Goats, Tortoises, Horses.
- Step 1: Categorize all the items into sets (Here, its pets): Indoor pets: Cats, Hamsters, and, Parrots. Outdoor pets: Horses, Tortoises, and Goats. Both categories (outdoor and indoor): Rabbits and Fish.
- Step 2: Draw a rectangle and label it as per the correlation between the two sets. Here, let's label the rectangle as Pets.
- Step 3: Draw the circles according to the number of categories you have. There are two categories in the sample question: outdoor pets and indoor pets. So, let us draw two circles and make sure the circles overlap.
- Step 4: Place all the pets in the relevant circles. If there are certain pets that fit both the categories, then place them at the intersection of sets, where the circles overlap. Rabbits and fish can be kept as indoor and outdoor pets, and hence they are placed at the intersection of both circles.
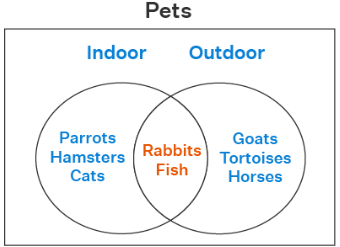
- Step 5: If there is a pet that doesn't fit either the indoor or outdoor sets, then place it within the rectangle but outside the circles.
Venn Diagram Formula
For any two given sets A and B, the Venn diagram formula is used to find one of the following: the number of elements of A, B, A U B, or A ⋂ B when the other 3 are given. The formula says:
- n(A U B) = n(A) + n(B) – n (A ⋂ B)
Here, n(A) and n(B) represent the number of elements in A and B respectively. n(A U B) and n(A ⋂ B) represent the number of elements in A U B and A ⋂ B respectively. This formula is further extended to 3 sets as well and it says:
- n (A U B U C) = n(A) + n(B) + n(C) - n(A ⋂ B) - n(B ⋂ C) - n(C ⋂ A) + n(A ⋂ B ⋂ C)
Here is an example of Venn diagram formula.
Example: In a cricket school, 12 players like bowling, 15 like batting, and 5 like both. Then how many players like either bowling or batting.
Solution: Let A and B be the sets of players who like bowling and batting respectively. Then
n(A) = 12
n(B) = 15
n(A ⋂ B) = 5
We have to find n(A U B). Using the Venn diagram formula,
n(A U B) = n(A) + n(B) – n (A ⋂ B)
n(A U B) = 12 + 15 - 5 = 22.
Applications of Venn Diagram
There are several advantages to using Venn diagrams. Venn diagram is used to illustrate concepts and groups in many fields, including statistics, linguistics, logic, education, computer science, and business.
- We can visually organize information to see the relationship between sets of items, such as commonalities and differences, and to depict the relations for visual communication.
- We can compare two or more subjects and clearly see what they have in common versus what makes them different. This might be done for selecting an important product or service to buy.
- Mathematicians also use Venn diagrams in math to solve complex equations.
- We can use Venn diagrams to compare data sets and to find correlations.
- Venn diagrams can be used to reason through the logic behind statements or equations.
|
144 videos|104 docs|61 tests
|




















