Venn Diagrams & Operations on Sets | Mathematics (Maths) Class 11 - Commerce PDF Download
| Table of contents |

|
| Introduction |

|
| Representation of Sets in a Venn Diagram |

|
| Operations on Venn Diagrams |

|
| Operations on Sets |

|
| Some Important Results |

|
Introduction
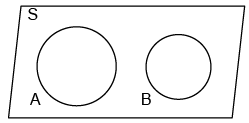
A Venn diagram is a diagrammatic representation of all the possible relationships between different sets of a finite number of elements. A Venn diagram is also known as a Primary diagram, Set diagram or Logic diagram.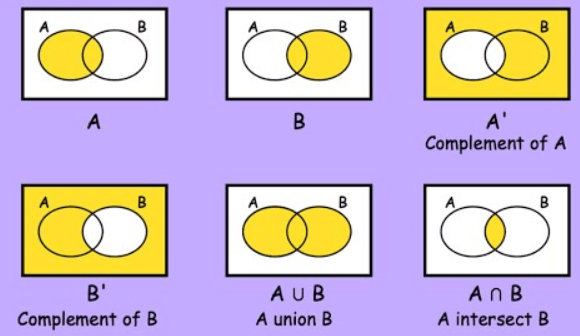
Fig: Venn Diagrams for Set A and B
Representation of Sets in a Venn Diagram
It is done as per the following:
- Each individual set is represented by a circle and enclosed within a quadrilateral (the quadrilateral represents the finiteness of the Venn diagram as well as the Universal set.)
- Labeling is done for each set with the set’s name to indicate difference and the respective constituting elements of each set are written within the circles.
- Sets having no element in common are represented separately while those having some of the elements common within them are shown with overlapping.
- The elements are written within the circle representing the set containing them and the common elements are written in the parts of circles that are overlapped.
Operations on Venn Diagrams
Just like the mathematical operations on sets like Union, Difference, Intersection, Complement, etc. we have operations on Venn diagrams that are given as follows:(i) Union of Sets
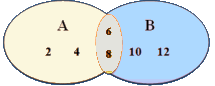
Let A = {2, 4, 6, 8} and B = {6, 8, 10, 12}. Represent A∪B through a well-labeled Venn diagram.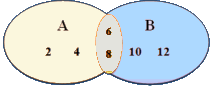
The orange colored patch represents the common elements {6, 8} and the quadrilateral represents
A ∪ B.
Properties of A U B
- The commutative law holds true as A ∪ B = B ∪ A
- The associative law also holds true as (A ∪ B) ∪ C = A ∪ (B ∪ C)
- A ∪ φ = A (Law of identity element)
- A ∪ A = A (Idempotent law)
- Law of the Universal Set - A ∪ U = U
(ii) The Intersection of Sets
An intersection is nothing but the collection of all the elements that are common to all the sets under consideration. Let A = {2, 4, 6, 8} and B = {6, 8, 10, 12} then A ∩ B is represented through a Venn diagram as per following:The orange colored patch represents the common elements {6, 8} as well as the A ∩ B. The intersection of 2 or more sets is the overlapped part(s) of the individual circles with the elements written in the overlapped parts.
Example:
Properties of A ∩ B
- Commutative law – A ∩ B = B ∩ A
- Associative law – (A ∩ B)∩ C = A ∩ (B ∩ C)
- φ ∩ A = φ
- U ∩ A = A
- A ∩ A = A (Idempotent law)
- Distributive law – A ∩ (B ∩ C) = (A ∩ B) U (A ∩ C)
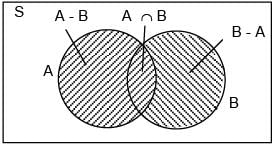
(iii) Difference of Sets
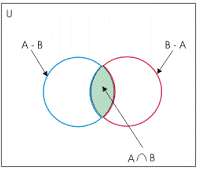
The difference of set A and B is represented as: A – B = {x : x ϵ A and x ∉ B} {converse holds true for B – A}.
Let, A = {1, 2, 3, 4, 5, 6} and B = {2, 4, 6, 8} then,
A – B = {1, 3, 5} and B – A = {8}.
The sets (A – B), (B – A) and (A ∩ B) are mutually disjoint sets.
It means that there is NO element common to any of the three sets and the intersection of any of the two or all the three sets will result in a null or void or empty set.
Some important results
- A - B ≠ B - A
- A - B ⊆ A 𝒂𝒏d B − A ⊆ B
- A-∅ = A 𝒂𝒏d A − A = ∅
(iv) Complement of Sets
The complement of a set A is the set of all the elements which are the elements of the universal set but not the elements of the A. It is represented by symbol A' or Ac.
Mathematically, A’ = U – A
Alternatively, the complement of a set A, A’ is the difference between the universal set U and the set A. Example: Let universal set U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and set A = {1, 3, 5, 7, 9}, then the complement of A is given as A’ = U – A = {2, 4, 6, 8, 10}

Properties Of Complement Sets
- A ∪ A’ = U
- A ∩ A’ = φ
- De Morgan’s Law – (A ∪ B)’ = A’ ∩ B’ Or (A ∩ B)’ = A’∪ B’
Let's try to prove this expression.
Left hand side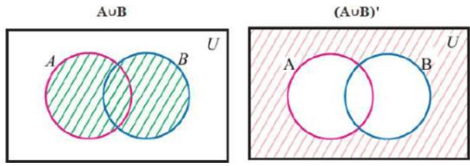
Right hand side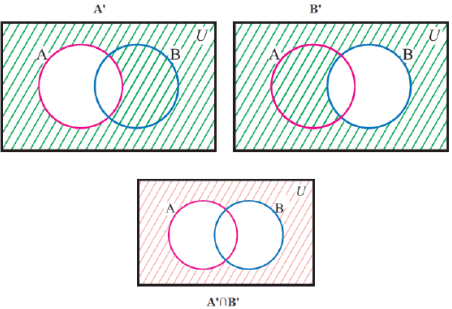
As the last image of both left hand side and the right hand side is same
Hence,this proves that (A ∪ B)’ = A’ ∩ B’.
- Double complement law : (A’)’ = A
- φ’ = U
- U’ = φ
Example
Q: Represent the Universal Set (U) = {x : x is an outcome of a dice’s roll} and set A = {s : s ϵ Even numbers} through a Venn diagram.Ans. Since, U = {1, 2, 3, 4, 5, 6} and A = {2, 4, 6}. Representing this with a Venn diagram we have:
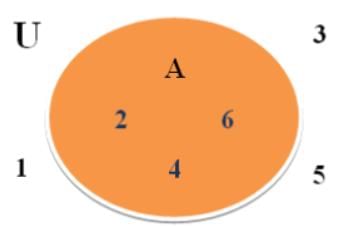
Here, A is a subset of U, represented as – A ⊂ U or
U is the super set of A, represented as – U ⊃ A
If A = {1, 2, 3, 4, 5} and B = {4, 5, 6, 7, 8}, then represent A – B and B – A through Venn diagrams.
A – B = {1, 2, 3}
B – A = {6, 7, 8}
Representing them in Venn diagrams:
a. A-B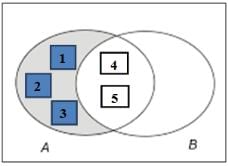 b. B-A
b. B-A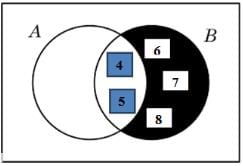
Operations on Sets
The important operations on sets are:
(i) Union
Now, we can define the following new set.
X ∪ Y = {z | z ∈ X or z ∈ Y}
(That is, z may be in X or in Y or in both X and Y)
X ∪ Y is read as "X union Y"
Now that X ∪ Y contains all the elements of X and all the elements of Y and the figure given below illustrates this.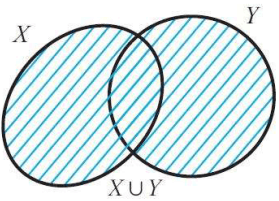
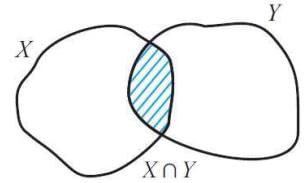
(ii) Intersection
Let X and Y be two sets.Now, we can define the following new set.
X ∩ Y = {z | z ∈ X and z ∈ Y}
(That is z must be in both X and Y)
X ∩ Y is read as "X intersection Y"
Now that X ∩ Y contains only those elements which belong to both X and Y and the figure given below illustrates this.
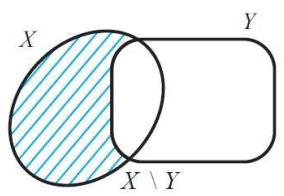
(iii) Set difference
Let X and Y be two sets.Now, we can define the following new set.
X\Y = {z | z ∈ X but z ∉ Y}
(That is z must be in X and must not be in Y)
X\Y is read as "X difference Y"
Now that X\Y contains only elements of X which are not in Y and the figure given below illustrates this.
Some authors use A - B for A\B. We shall use the notation A \ B which is widely used in mathematics for set difference.
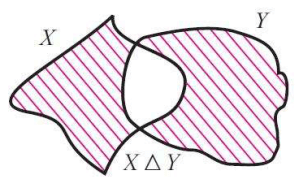
(iv) Symmetric difference
Let X and Y be two sets.Now, we can define the following new set.
X Δ Y = (X\Y) ∪ (Y\X)
X Δ Y is read as "X symmetric difference Y"
Now that X Δ Y contains all elements in X∪Y which are not in X∩Y and the figure given below illustrates this.
(v) Complement
If X ⊆ U, where U is a universal set, then U\X is called the compliment of X with respect to U.
If underlying universal set is fixed, then we denote U\X by X' and it is called compliment of X.
X' = U\X The difference set set A\B can also be viewed as the compliment of B with respect to A.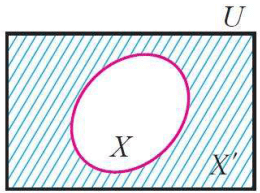
That means if x ∈ A ⇒ x ∉ A’ and x ∈ A’ ⇒ x ∉ A
(vi) Disjoint sets
Two sets X and Y are said to be disjoint if they do not have any common element. That is, X and Y are disjoint if X ∩ Y = ϕIt is clear that n(A ∪ B) = n(A) + n(B), if A and B are disjoint finite set.
(i) n ( A ∪ B) = n (A) + n (B) - n ( A ∩ B)
(ii) n(A ∪ B) = n(A - B) + n(B - A) + n(A ∩ B)
(iii) n (A) = n (A - B) + n ( A ∪ B)
(iv) n (B) = n (B - A ) + n ( A ∪ B)
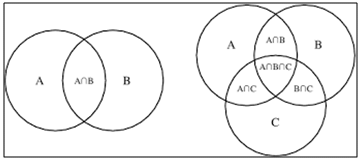
If there three sets A,B and C then
𝑛(A ∪ B ∪ C) = 𝑛(A) + 𝑛(B) + 𝑛(C) − 𝑛(A ∩ B) − 𝑛(B ∩ C) − 𝑛(C ∩ A) + 𝑛(A ∩ B ∩ C)
Note: But students are advised to do questions having three sets with venn diagramSome Important Results
Some Important Results
- A - B = A ∩ Bc where Bc is complement of B
- (A - B) ∪ B = A ∪ B
- (A - B) ∩ B = ∅
- A ⊆ B ⇔ Bc ⊆ Ac
- A - B = Bc − Ac
|
73 videos|264 docs|91 tests
|
FAQs on Venn Diagrams & Operations on Sets - Mathematics (Maths) Class 11 - Commerce
| 1. What is the significance of using Venn diagrams in representing sets? |  |
| 2. How are operations on sets performed using Venn diagrams? |  |
| 3. How do Venn diagrams help in solving problems related to Airforce X Y / Indian Navy SSR exams? |  |
| 4. Are Venn diagrams commonly used in competitive exams like Airforce X Y / Indian Navy SSR? |  |
| 5. How can I improve my understanding of Venn diagrams and operations on sets for the Airforce X Y / Indian Navy SSR exam? |  |