Very Short Answers - Number System Class 9 Notes | EduRev

Q.1. What is the value of (2³)²?
Solution. 
(2³)² = 2^3x2           [∵ (x^m)ⁿ = x^m.n]
= 2⁶ =2 x 2 x 2 x 2 x 2 x 2 = 64

Q.2. What is the value of (625) ^1/4 ?
Solution.


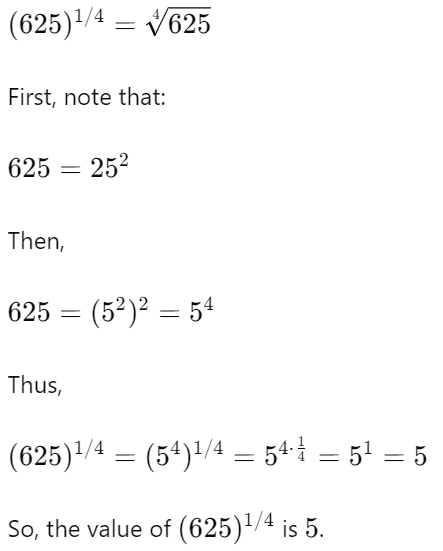
Q.3. Which of the following are irrational numbers?
√3, √4, √5, 22/7, π, 0 
Solution.  √3, √5 and π are irrational numbers.

Q.4. Which of the following are rational?
2√3, 1, 0, 3.14, π, 22/7

Solution. 1, 0, 3.14 and 22/7 are rational numbers.

Q.5. Which of the following cube roots is not irrational?
3 √5, 3√6, 3√7, 3√8, 3√9
Solution.  3√8 is not an irrational number.


Q.6. Which three integers are equal to their own cube roots?
Solution. –1, 0 and 1
[∵ 3√-1 = -1, 3√1 = 1 and 3√0 = 0 ]  

Q.7. Is the following number rational or irrational? 0.0769230769230769230...
Solution.
The given number is rational.      [∵ “076923” repeats]

Q.8. Is 0.666 ...a “non-terminating rational” or “non-terminating recurring rational number”?
Solution. Non-terminating rational number.

Q.9. Is 1.27 27 27 ... non-terminating recurring or non-terminating non-recurring number?
Solution. It is a non-terminating recurring rational number.

Q.10. The decimal representation of √3 is 1.73205807... . Is it non-terminating nonrecurring?
Solution. Yes

Q.11. Is the product of a rational and an irrational number, rational?
Solution. No. It is an irrational number.

Q.12. Write the smallest non-negative integer.
 Solution. ‘0’ Question

Q.13. Write the smallest positive integer.
Solution. 1 Question 

Q.14. Up to how many decimal places, π and 22/7  are same?
Solution. π and 22/7 are same only up to 2 decimal places.
[∵ 22/7  = 3.142857142... and π =3.141592653589...]

Q.15. Which of the following is irrational?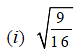

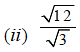
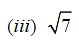
Solution. √7 is irrational.

Q.16. Which of the following is the value of 0.999... expressed as p/q : 
(i) 9/10
(ii)  1
(iii)   999/1000
Solution. 0.999... = 1

Q.17. What is a terminating decimal?
Solution. The number with a finite decimal part are known as terminating decimal.
Example: 0.375 is a terminating decimal.
Note: If we express a rational number as a decimal number and remainder becomes zero after certain stage, then the decimal expansion is terminating.