Class 9 Maths Question Answers - Polynomials
Q.1. What is p(–2) for the polynomial p(t) = t2 – t + 1?
Solution. p(t) = t2 – t + 1
⇒ p(–2) = (–2)2 – (–2) + 1
= 4 + 2 + 1
= 7
Q.2. If x - 1/x = -1 then what is
Solution. On squaring both sides we get;
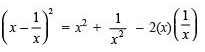
⇒
⇒
⇒
Q.3. If x + y = –1, then what is the value of x3 + y3 – 3xy?
Solution. We have x3 + y3 = (x + y)(x2 – xy + y2)
⇒ x3 + y3 = (–1)(x2 + 2xy + y2) + 3xy
⇒ x3 + y3 = –1(x + y)2 – 3xy
⇒ x3 + y3 – 3xy = –1(–1)2 = –1(1)
⇒ x3 + y3 – 3xy = –1
Q.4. Show that p(x) is not a multiple of g(x), when p(x) = x3 + x – 1 g(x) = 3x – 1
Solution. g(x) = 3x – 1 = 0 ⇒ x = 1/3
∴ Remainder
Since remainder ≠ 0, so p(x) is not a multiple of g(x).
Q.5. (a) Find the value of ‘a’ if x – a is a factor of x3 – ax2 + 2x + a – 5.
(b) Find the value of ‘a’, if (x – a) is a factor of x3 – ax2 + 2x + a – 1
[NCERT Exemplar]
(c) If x + 1 is a factor of ax3 + x2 – 2x + 4a – 9 find the value of ‘a’. [NCERT Exemplar]
Solution. (a) Let p(x) = x3 – ax2 + 2x + a – 5
since x – a is a factor of p(x),
so p(a) = 0
⇒ (a)3 – a(a)2 + 2(a) + a – 5 = 0
⇒ (a)3 – a(a)2 + 2(a) + a – 5 = 0
⇒ 3a – 5 = 0 ⇒ a =
(b) Here, p(x) = x3 – ax2 + 2x + a – 1
∵ x – a is a factor of p(x)
∴ p(a) = 0
⇒ a3 – a(a)2 + 2(a) + a – 1 = 0
⇒ a3 – a3 + 2a + a – 1 = 0
⇒ 3a – 1 = 0
⇒ a = 1/3
(c) Here, x + 1 is a factor of p(x) = ax3 + x2 – 2x + 4a – 9
∴ p(–1) = 0
⇒ a(–1)3 + (–1)2 – 2(–1) + 4a – 9 = 0
⇒ –a + 1 + 2 + 4a – 9 = 0
⇒ 3a – 6 = 0
⇒ a = 2
Q.6. Without finding the cubes factorise (a – b)3 + (b – c)3 + (c – a)3.
Solution. If x + y + z = 0
then x3 + y3 + z3 = 3xyz
Here, (a – b) + (b – c) + (c –a) = 0
∴ (a – b)3 + (b – c)3 + (c – a)3
= 3(a – b)(b – c)(c – a)
Q.7. What is zero of a non-zero constant polynomial?
Solution. A non-zero constant polynomial has no zero.
Q.8. What is the coefficient of a zero polynomial?
Solution. A zero polynomial has all coefficients zero.
Q.9. What is the degree of a biquadratic polynomial?
Solution. ∵ The degree of a quadratic polynomial is 2.
∴ The degree of a biquadratic polynomial is 4.
Q.10. Is the statement: ‘0’ may be a zero of polynomial, true?
Solution. Yes, this statement is true.
Q.11. What is the value of (x + a) (x + b)?
Solution. The value of (x + a) (x + b)
= x2 + (a + b) x + ab.
Q.12. What is the value of (x + y + z)2 – 2[xy + yz + zx]?
Solution. ∵ (x + y + z)2
= x2 + y2 + z2 + 2 xy + 2 yz + 2 zx
= x2 + y2 + z2 + 2[xy + yz + zx]
∴ (x + y + z)2 – 2[xy + yz + zx]
= x2 + y2 + z2
Q.13. What is the value of (x + y)3 – 3xy (x + y)?
Solution. ∵ (x + y)3 = x3 + y3 + 3xy (x + y)
∴ [x3 + y3 + 3xy (x + y)] – [3xy (x + y)] = x3 + y3
⇒ (x + y)3 – 3xy(x + y) = x3 + y3
Thus, value of x3 + y3 is (x + y)3 – 3xy (x + y)
Q.14. Write the value of x3 – y3.
Solution. The value of x3 – y3 is (x – y)3 + 3xy (x – y)
Q.15. Write the degree of the polynomial 4x4 + ox3 + ox5 + 5x + 7?
Solution. The degree of 4x4 + 0x3 + 0x5 + 5x + 7 is 4.
Q.16. What is the zero of the polynomial p(x) = 2x + 5?
Solution. ∵ p(x) = 0 ⇒ 2x + 5 = 0
⇒ x =
∴ zero of 2x + 5 is
Q.17. Which of the following is one of the zero of the polynomial 2x2 + 7x – 4 ?
2, -2 ?
Solution. ∵ 2x2 + 7x – 4 = 2x2 + 8x – x – 4
⇒ 2x (x + 4) – 1 (x + 4) = 0
⇒ (x + 4) (2x – 1) = 0
⇒ x = – 4, x = 1/2,
∴ One of the zero of 2x2 + 7x – 4 is 1/2.
Q.18. If a + b + 2 = 0, then what is the value of a3 + b3 + 8.
Solution. ∵ x + y + z = 0
⇒ x3 + y3 + z3 = 3xyz
∴ a + b + 2 = 0
⇒ (a)3 + (b)3 + (2)3 = 3(a × b × 2) = 6ab
⇒ The value of a3 + b3 + 8 is 6ab
Q.19. If 49x2 – p =, what is the value of p?
Solution. 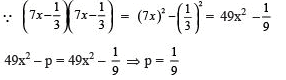
Q.20. If = 1, then what is the value of
?
Solution. On squaring both the sides we get;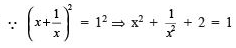
|
40 videos|471 docs|57 tests
|
FAQs on Class 9 Maths Question Answers - Polynomials
| 1. What is a polynomial? |  |
| 2. How to determine the degree of a polynomial? |  |
| 3. Can a polynomial have negative exponents? |  |
| 4. What is the difference between a monomial and a polynomial? |  |
| 5. How to perform polynomial division? |  |

















