Vibration Isolation | Theory of Machines (TOM) - Mechanical Engineering PDF Download

Vibrations Causing Unbalanced Forces in a Mechanical Running System

1. Rotating Unbalance
(Rotors, whose C.G. is not coinciding with the axis of shaft).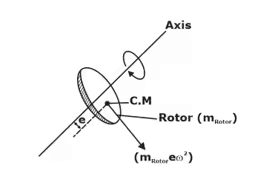
At time, t
f_un in a particular direction,
f_un = (M_Rotor eω²)
where, f₀ = (m_Rotor eω²) — max volume of unbalanced force.
ω — force frequency or excitation.

2. Reciprocating Unbalance: (in Piston-crank)
f_un = m_Rrω² sinθ
[m_R—mass of Reciprocating Ports]
(mass of Piston + mass of crosshead + mass of connecting Rod)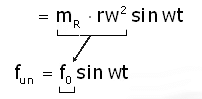

Where, ω = forced frequency and m = machine mass (whole) which is under vibrations.

3. Forced-Damped Systems (Perfect Reality)

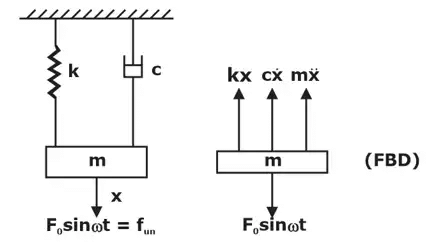Forced vibrations of a damped spring mass system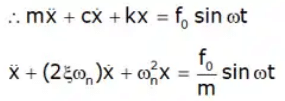
This is the equation of forced-Damped System.
∴ The solution will be, x = c · f + P · I
After some time, CF = 0

After solving,

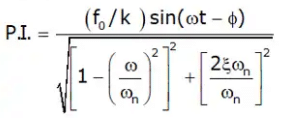
Amplitude of forced vibrations (A):

Hence, x = PI
∴ x = A sin(ωt - ϕ)
Where,  A = Amplitude of steady state vibrations (independence of time) (forced vibrations)
Running system vibrations will never stop.
Every machine/mechanical running system must have one running life.

4. Magnification factor (M.F.)

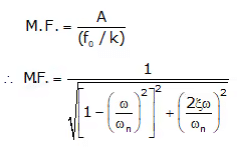
∴ M.F. depends upon:
(i) ω/ω_n
(ii) ζ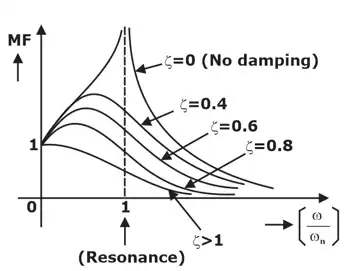
Magnification Factor

• As Underdamping Increases
  ⇒ ζ↓
  ⇒ MF ↑ ⇒ A↑
  ⇒ Running life decrease ↓
• At Resonance
  [ω/ω_n = 1]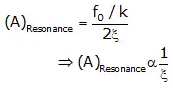
  

Note: At some time 't',
F = f₀sin[ωt]
x = Aω cos ωt
= Aω[sin{π/2 + (ωt - ϕ)}]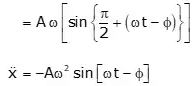

The Basic Equation was,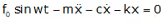

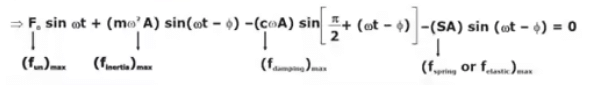
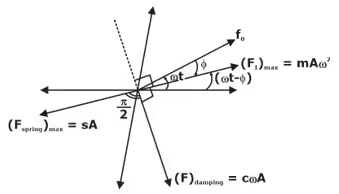
• Spring and damping force’s max values are perpendicular to each other.
• Inertia force lies exactly opposite (At 180°) To the spring force’s max value.

6. Vibration Isolations
It is used to isolate the ground from the vibrations of the Running machine so as to save other stationary m/cs from these vibration effects.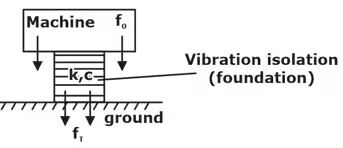
Vibration Isolation

F_τ = force transmitted to the ground
F_τ < < < < < F₀
∈ = F_τ / F₀ = Transmissivity
0 < ∈ < 1
∈ → 0 (for Belts)
Now, F_τ = Resultant of forces of spring force and damping force (max values)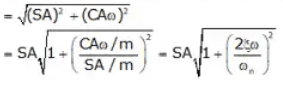


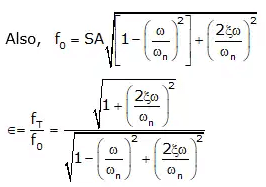
Hence, ′∈′ depends upon:
(i) ω/ω_n
(ii) ζ
Note: If, w/w_n = 0 w/w_n = √2 ⇒ ∈ = 1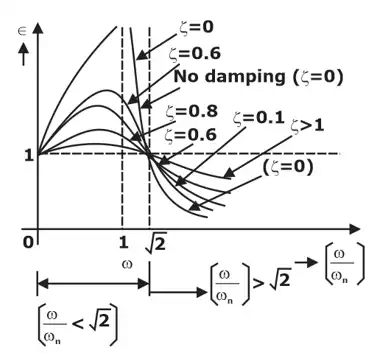

• As Underdamping ↑ ⇒ ζ↓
  
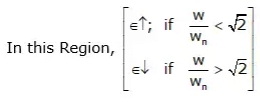
  ∈ will be constant, if w/w_n = √2
• Vibration Isolation is Effective 
  When ∈ < 1
  ⇒ (w/w_n > √2) → called "Effective Vibration-isolation-zone".
• In Effective Vibration Isolation Zone:
  w/w_n > √2; Then At ζ = 0, e is minimum.
  ∴ No damping → is Best. (∵ = ∈ → 0 Best)
  Hence, Damping is dangerous in this Zone.
  ⇒ Ass ↑ (in this zone). ∈↑ ⇒ f_τ ↑