Werner’s Theory & 18 Electron Rule | Inorganic Chemistry PDF Download
WeRNER’S THEORY
In 1983 Werner produced a theory of coordination compounds to explain the structures and formation of compounds. Werner was the first inorganic chemist to be awarded the Nobel prize for chemistry in 1913. Werner postulated that metals exhibit two types of valencies:
(1) Primary valence and
(2) secondary valence.
In modern terminology, primary valence corresponds to the oxidation number and secondary valency to coordination number of metal.
The primary valence is ionisable and non-directional. The primary valency must be satisfied only by negative ions as in simple salts such as CoCl3.
Primary valency of cobalt in [Co(NH3)6]Cl3, [Co(NH3)5Cl]Cl2, [Co(NH3)4Cl2]Cl and [Co(NH3)3Cl3] complexes is +3 and is satisfied by three Cl– ions. The anions which satisfy only primary valency are written outside the coordination sphere. The anions may satisfy primary as well as secondary valencies of metal. The anions satisfying the primary valency do not give any geometry to complex compounds. When the compound undergoes ionization in aqueous solution, the anions which aqueous solution, three Cl– ions which satisfy primary valency are obtained.
The secondary or auxiliary valencies of metal are satisfied either by negative ions or neutral molecules or both. In the structure of coordination compounds the metal cation and the species satisfying the secondary valencies are placed inside the coordination compounds the metal cation and the species satisfying the secondary valencies are placed inside the coordination sphere. The species satisfying secondary valencies are not obtained in aqueous solution in free state instead a complex ion is obtained. The secondary valencies are directed in space to give a definite geometry to the complex. The geometries of complexes corresponding to 2, 3, 4 and 6 secondary valencies are linear, trigonal planar, tetrahedral or square planar and octahedral respectively.
Werner studied the structure and properties of the following four complexes of Co(III) chloride with ammonia which have different colours.
Table 1. Complexes of Co(III) Chloride with Ammonia.
Werner treated the first four complexes of Co(III) given in Table 1, with an excess of AgNO3. The white precipitate of AgCl were obtained in different amount:
Werner reported that in CoCl3.6NH3 all the three chlorides satisfy only primar y valence and the six ammonia molecules satisfy only the secondary valency. The primary valencies represented by dotted lines (...) and secondary valencies are represented by solid line ( —). The structure of CoCl3·6NH3 is shown in figure 1 (a). This compound in aqueous solution gives total number of four ions i.e. three Cl– and one [Co(NH3)6]3+ ions. Thus, in modern term this compound is written as [Co(NH3)6]Cl3. When this compound is treated with an excess of AgNO3 solution, all three Cl– ions are precipitated as AgCl.
In CoCl3·5NH3, the primary and the secondary valencies of cobalt are three and six respectively. All the three primary valencies are satisfied by three chloride ions. Out of six secondary valencies, five are satisfies by ammonia molecules and the sixth by one of the chloride ions. Therefore, one chloride ion exhibit double duty as it satisfy a primary as well as a secondary valency and it is represented as line. [Fig. 1(b)]. When this compound is treated with an excess of AgNO3 solution, only two chloride ions are precipitated as AgCl.
This indicates that t he Cl– ions which satisfy only the primary valencies are ionisable. In aqueous solution total number of three ions are obtained i.e., one [Co(NH3)5Cl]2+ and two Cl– ions. In modern term this compound is written as [Co(NH3)5Cl]Cl2. The structure of [Co(NH3)5Cl]Cl2 is shown in Fig. 1(b).
In CoCl3·4NH3, the primary and secondary valencies of cobalt are 3 and 6 respectively. All the three primary valencies are satisfied by three chloride ions. Out of six secondary valencies, four are satisfied by ammonia molecules with fifth and sixth by two of the three chloride ions. Thus, two chloride ions exhibit double duty of satisfying primary as well as secondary valencies. When this compound is treated with an excess of AgNO3 solution, only one chloride ion is precipitated as AgCl. In aqueous solution this compound gives total number of two ions. i.e., one [Co(NH3)4Cl2]+ and one Cl– ion. This compound is written as [Co(NH3)4Cl2]Cl. The structure of this compound is shown in Fig. 1(c).
In CoCl3.3NH3, primary and the secondary valencies of cobalt are three and six respectively. All the three primary valencies are satisfied by three chloride ions. Out of six secondary valencies, three are satisfied by three ammonia molecules and three by chloride ions. In this compounds three chloride ions satisfy primary as well as secondary valencies. This compound does not give any precipitate with AgNO3 solution. This compound is a neutral molecule and does not given any ion in aqueous solution. In modern term this compound is written as [Co(NH3)3Cl3]. The structure of this compound is shown in Fig. 1(d).
Werner also attempted to find the geometries of isomers of the complexes of Co(III), Cr(III), Cu(II), pt(II) etc. The various geometries for complexes of coordination no. 6 are hexagonal planar, trigonal prismatic and octahedral (Fig. 2).
Fig. 2.
The possible isomers for the ammine complexes of Co(III) for all the three geometries are given in the Table 2:
Complex | Theoretical | Observed | ||
Hexagonal Planar | Trigonal Prismatic | Octahedral | ||
[Co(NH3)6]3+ [Co(NH3)5Cl]2+ [Co(NH3)4Cl2]+ [Co(NH3)3Cl3] | 1 | 1 1 3 3 | 1 1 2 2 | 1 1 2 2 |
Fig. 3.(a) Three possible isomers for hexagonal planar geometry.
Fig. 3.(b) Three possible isomers for hexagonal planar geometry.
Fig. 3.(c) Three possible isomers for hexagonal planar geometry.
Consider the coordination compound [Co(NH3)4Cl2]Cl. Werner suggested that this compound may exist in three possible geometries i.e., hexagonal planar, trigonal prismatic and octahedral. The possible isomers corresponding to these geometries are three, three and two respectively as shown in Figure 1.3.
Only two isomers of compound [Co(NH3)4Cl2]Cl have been isolated which correspond to the octahedral geometry. Thus, in these isomers the arrangement of ligands round the metal cation is octahedral. Werner concluded that the complexes of coordination number 6 are octahedral.
Werner also suggested that the coordination compounds with coordination number 4 exhibit two possible geometries i.e., square planar and tetrahedral.
In coordination compound [Pt(NH3)4Cl2], coordination number is 4 and this compound exhibits square planar geometry. Two isomers cis– and trans– [Pt(NH3)4Cl2] has been isolated for this compound (Figure 1.4).
Fig. 4. cis- and trans-isomer of [Pt(NH3)2Cl2].
Werner also suggested that in tetrahedral complexes only one arrangement is possible round the metal cation.
Evidence in Favour of Werner’s Theory
(1) Electrical Conductance Measurement: Molar conductance of a substance depends upon the number of charges on the particles furnished by the substance in aqueous solution. As the number of particles (i.e., ions) and charges on them increases, the molar conductance of the compound increases. The observed molar conductance for aqueous solutions of cobalt(III) chloride complexes with ammonia decreases in the order.
[Co(NH3)6]Cl3 > [Co(NH3)5Cl]Cl2 > [Co(NH3)4Cl2]Cl > [Co(NH3)3Cl3]
This indicates that the number of ions and the number of charges decrease in the same order as shown in the table 1.3. The molar conductance measurement of Co(III) chloride complexes with ammonia suggest the structures similar to structure suggested by Werner.
Table 3. Elucidation of Structure of Co(III) and Pt(IV) Complexes on the Basis of Conductance and Cryoscopic Measurements.
Compound | No. of Particles Determined from Cryoscopic Measurement | No. of Electrical Charges Determined from conductance Measurement | Structure of the Compound |
CoCl3 · 6NH3 CoCl3 · 5NH3 CoCl3 · 4NH3 CoCl3 · 3NH3 PtCl4 · 6NH3 PtCl4 · 5NH3 PtCl4 · 4NH3 PtCl4 · 3NH3 PtCl4 · 2NH3 | 4 | 6 (+3, –1) 4 (+2, –1) 2 (+1, –1) 0 8 (+4, –1) 6 (+3, –1) 4 (+2, –1) 2 (+1, –1) 0 | [Co(NH3)6]3+ 3Cl– 4Cl– [Pt(NH3)5Cl]3+ 3Cl– [Pt(NH)4Cl2]2+ 2Cl– [Pt(NH3)3Cl3]+ Cl– [Pt(NH3)2Cl4]0 |
(2) Cryoscopic Measurement: The depression in freezing point is a colligative property and depends upon the number of particles in the solution. Greater the number of particles, more will be the depression in freezing point. If a species dissociates into two, three, four, ... ions, then depression in freezing point will be twice, three times, four times, .... respectively as compared to the expected depression for single species. Thus, cryoscopic measurement (i.e., measurement of depression in freezing point) gives the number of ions furnished by the dissociation of an ionic compound. The cryoscopic measurement indicates that CoCl3.3NH3 remains undissociated (see table 3).
(3) Precipitation Reaction: The number of ions furnished by a coordination compound can also be determined by precipitation reactions. When the complexes CoCl3.6NH3, CoCl3.5NH3 and CoCl3.4NH4 are treated with an excess of AgNO3 solution, the number of chloride ions precipitated as AgCl is 3, 2 and 1 respectively. Thus indicates that the number of chloride ions in ionization sphere are 3, 2 and 1 respectively. The structures provided by precipitation reactions are similar to those given by Werner. The complex CoCl3.3NH3 gives no precipitate with AgNO3 solution. This indicates that all the three Cl– ions are present in the coordination sphere in this compound. Electronic spectra (UV-visible) and X-rays spectroscopy are the recent methods to determine the structure of complexes. Electronic spectra give the information about the energies of orbitals, shapes of complexes (i.e., either the complex is octahedral or distorted octahedral or tetrahedral). X-rays spectroscopy gives the information about the structure of complex, bond lengths and bond angles. Magnetic moment measurement gives the information about the complexes viz. Either the complex is tetrahedral or square planar or octahedral.
Illustrative Example: An isomer of CrCl3 6H2O reacts with one mole AgNO3 to give one mole of precipitate of AgCl. What is the compound?
Answer. Only those ions which are present outside the coordination sphere can be ionised.
[CrCl2(H2O)4]Cl . H2O + AgNO3 → AgCl
18. Sidgwick concept of Coordinate Bond According to Sidgwick’s concept the ligands donate electron pairs to the metal cation or atom resulting in the formation of the coordinate bonds between metal and the ligands which is represented as M ← L.
Therefore, the complex ion, [Co(NH3)6]3+ can be written as:
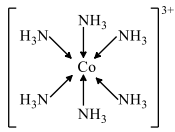
The donation of an electron pair by N atom of Nh3 has been represented by an arrow. The coordination bond is very similarly covalent bond.
Limitations of Sidgwick’s Concept: The donation of one electron pair by each ligand to the central metal cation atom to form M ← L coordinate bonds cause the accumulation of negative charge on the central metal cation atom. Due to accumulation of a negative charge on the metal cation or atom, a partial ionic character is created in the complex making it less stable. According to Pauling’s electroneutrality principal, the metal ligand bonds have some ionic character.
To prevent the accumulation of negative charge in metal cation or atom, either the bond pair of electrons must be attracted more strongly to the donor atoms of the ligands or in addition to the σ-bond there should be metal to ligand π-bonding.
19. Effective Atomic Number (EAN) Rule: The effective atomic number of metal cation or atoms in complex is the sum of electrons on metal and the electros donated by the ligands. According to Sidgwick’s effective atomic number (EAN) rule, the EAN of metal equal to the atomic number of next inert gas i.e., equal to 36 (Kr), 54 (Xe) or 85 (Rn). For example, EAN [Co(NH3)6[3+ can be calculated following:
Number of electrons on Co atom = 27
Number of electrons in Co3+ ion = 27 – 3 = 24
Number of electrons donated by six NH3 ligands = 2 × 6 = 12
EAN of Co3+ in [Co(NH3)6]3+ = 24 + 12 = 36
20. 18 electron rule An alternate and more general rule is the 18 electron rule. According to this rule, in a complex the sum of valence electrons and the electrons donated by the ligands is 18. It provides a closed and stable configuration, ns2 (n – 1) d10 np6.
For example: For [Co(NH3)6]3+
Valence shell electronic configuration of 27Co = 3d7 4s2
Valence shell electronic configuration of Co 3+ = 3d6 4s0
Number of electrons in valence shell of Co 3+ = 6
Number of electron donated by six NH3 molecules = 2 × 6 = 12
Number of valence electrons in [Co(NH3)6]3+ = 6 + 12 = 18e–
The complexes which follows the EAN or 18 electron rule are considered to be stable. EAN and 18 electron rules are similar but the 18 electron rule is more advantageous because there is no need to remember the atomic numbers of each noble gas. However, there are some exceptions which obey neither EAN or 18 electron rule. The complexes in which the metal cations or atoms have odd number of electrons never obey the EAN rule or 18 electron rule because the sum of total electrons or valence shell electrons and the electrons donated by the ligands is also an odd number. For example, consider the complex [Fe(CN)6]3–
For EAN Rule: Number of electrons on Fe atom = 26
Number of electron on Fe3+ ion = 23
Number of electrons donated by six CN– ligands = 2 × 6 = 12
EAN of [Fe(CN)6]3– 23 + 12 = 35
Thus, [Fe(CN)6]3– does not obey EAN rule.
For 18 Electrons Rule:
Valence shell electrons configuration of Fe atom = 3d6 4s2
Valence shell electronic configuration of Fe3+ ion = 3d5
Number of valence electron in Fe3+ ion = 5
Number of electrons donated by six CN– ligands = 2 × 6 = 12
Number of valence electrons in [Fe(CN)6]3– = 5 + 12 = 17
Thus, [Fe(CN)6]3– does not obey the 18 electron rule.
The complexes of d8 metals having coordination number of 4 also obey neither EAN rule nor 18 electron rule. For example, the complexes [NiCl4]2–, [Ni(CN)4]2–, [PdCl4]2–, [PtCl4]2– obey neither the EAN rule nor 18 electron rule.
|
50 videos|92 docs|41 tests
|
FAQs on Werner’s Theory & 18 Electron Rule - Inorganic Chemistry
| 1. What is Werner's theory and how does it relate to the 18 electron rule? |  |
| 2. How does the 18 electron rule help in understanding the stability of coordination compounds? |  |
| 3. Are there any exceptions to the 18 electron rule? |  |
| 4. How is Werner's theory relevant in coordination chemistry today? |  |
| 5. Can the 18 electron rule be applied to all coordination compounds? |  |

















