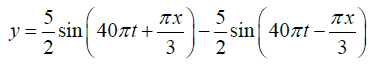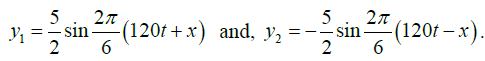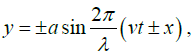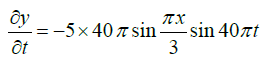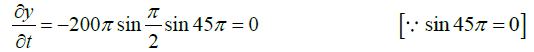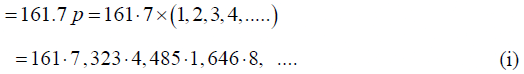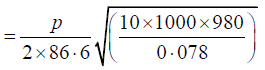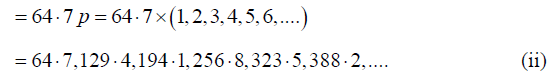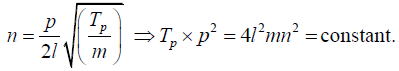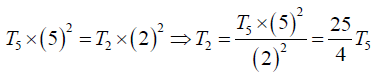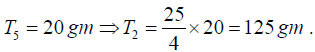Wave Motion: Assignment | Oscillations, Waves & Optics - Physics PDF Download
Q.1. Calculate the speed of transverse wave in a wire of radius 0.05cm under the tension produced by 1.0 kg-wt. The density of the material of wire is 3 9.8gm/cm3.
The speed of transverse waves in a string of mass m per unit length under a tension
T is given by
Here, T =1.0 kg-wt =1.0 x 9.8N [∵ 1kg-wt= g newton]
And, m = (πr2) x density
= 3.14 x (0.05 x 10-2m) x (9.8 x 103 kg/m3) = 7.7 x 10-5 kg/m.
Q.2. A flexible string of length 0.99m and mass 5 gm is stretched by a tension of T Newton. The string vibrates in five segments with a frequency of 1000 Hz. Calculate the tension in the string.
The frequency of a wire of length l, mass per unit length m, stretched under a
tension T and vibrating in p loops is given by
The tension is thus given by
Putting the given values, we get
Q.3. The dimensions of the membrane of a rectangular drum are 10cm x 20cm. It is stretched to a tension of 5kg/cm and its mass is 20 gm. What is the fundamental frequency?
The fundamental frequency of a rectangular membrane of sides a and b is given
by
Where T is the tension per unit length of the boundary of the membrane and M is the
mass per unit area of the membrane.
Here, T = 5kg/cm=5 x 1000 x 980dyne/cm, M = 20/(10 x 20)= 0.1gm/cm2
a = 10 cm and b = 20cm
Q.4. A wire under tension vibrates with a frequency of 450 per second. What would be the fundamental frequency if the wire was half as long, twice as thick and under one-fourth tension?
The frequency n of a wire of length l, mass per unit length m, stretched by a
tension T and vibrating in p segments, is given by
.... (1)
For emitting lowest characteristic frequency n = 450Hz it should vibrate in one segment i.e. p = . Also m =πr2d where r is the radius and d the density. Therefore, we have.....(2)
Now, let n' be the frequency when l is reduced to l/2, r is increased to 2r and T isreduced to T/4. Thus
Comparing with equation (i), we see that
Q.5. The two parts of a sonometer wire divided by a moveable knife-edge differ in length by 2mm and produce 1 beat per second when sounded together. Find their frequencies, if the whole length of the wire is 1 meter.
Let l1 and l2 be the lengths of the two parts of the sonometer wire and n1 and n2 their frequencies. Then
l1 + l2 = 100cm and, l1 - l2 = 2.0mm = 0.2cm.
Solving these two equations, we get l1 = 50.1cm and l2 = 49.9 cm
According to the law of length of stretched strings, we have n1l1 = n2l2:
But 1 beat is produced in 1 second, so that n2-n1 = 1 or n2 = n1+1.
Therefore n1l1 = (n1+l)l2.
Substituting the values of l1 and l2, we get n1 x 50.1 = (n1+ 1) x 49.9
or 50.1n1 - 49.9n1 = 49.9
⇒ 0.2n1 = 49.9
Q.6. In Melde’s experiment the string vibrates in 5 loops with a load of 20 gm. How much load will be required to make the string vibrate in 2 loops?
In Melde’s experiment the string vibrates with the fixed frequency n of the fork.
Hence if the length l is kept. If Tp be the tension required to produce p loops, we have
Therefore, if T5 and T2 be the tensions to produce 5 and 2 loops respectively, we have
Here,
Q.7. An open organ pipe is suddenly closed with the result that the second overtone of the closed pipe is found to be higher in frequency by 100 vibrations/s than the first overtone of the original pipe. What is the fundamental frequency of the open pipe?
The frequency of the open organ pipe is
where, n =1,2,..............
The first overtone frequency of the open organ pipe is
The frequency of the closed organ pipe iswhere, n =0,1,2,.............
The second overtone frequency of the closed organ pipe is
Given f1 - f2 = 100 vibration/sec
∴ Fundamental frequency of open pipe,
Q.8. Calculate the tensile stress in a steel wire of density 7.5gm/ cm3 when the velocity of transverse waves in the wire is 400m/s.
The transverse waves velocity is
So that the tension (force) in the wire of mass m per unit length is given by
T= v2m
If A be the area of cross-section of the wire, then
Now, m = A x ρ, where ρ is the density of the material of the wire.
= (400,000cm/sec2) x (7.5 gm/cm3)= 1.2 x 1010 dynes/cm2.
Q.9. Four violin strings, all of the same length and material, but of diameters in the ratio 4:3:2:1 are to be stretched so that each gives a note whose frequency is 3/2 times that of the preceding string. If the stretching force of the first string is 2.048kg-wt, calculate the tensions in the other strings.
Let T1, T2, T3, T4 be the tensions and 4r,3r,2r, r the radii of the four strings. Their
length l and density of material d are same. In view of the given data, let their
frequencies be respectively n, (3/ 2)n, (9/4)n and (27/8)n. Then we have
...(1)
...(2)
....(3)
And... (4)
Dividing equation (2) by (1), we have
Dividing equation (3) by (1), we have
Dividing equation (4) by (1), we have
Q.10. An open organ pipe sounding its fundamental note is in tune with a fork of frequency 439 cycles/s. How much must the pipe be shortened or lengthened in order that 2 beats shall be heard when it sounded with fork? Assume the speed of sound is 342 m/s.
The new frequency with the changed length L1 is f1= 439+2 = 441
The pipe must be shortened by 0.3895-0.3877=0.0018m or 1.8mm or lengthened by0.3913-0.3895 = 0.0018m = 1.8mm, so that 2 beats/s may be heard when it is sounded
with the fork.
Q.11. A string vibrates according to the equation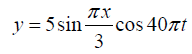
where x and y are in cm and t in second. Find out the amplitude and velocity of the two component waves whose superposition can give rise to this vibration. What is the distance between adjacent node? What is the velocity of a particle of the string at x=1.5cm at t = 9/8second?
The given equation
.....(1)
represents a stationary wave. It may be written as
The two sine terms represent two harmonic waves traveling in opposite directions. Thesetwo waves constitute the given stationary wave. The component waves may be written as
Comparing the component wave equations with the standard equation,
Amplitude a= 5/2cm, Wavelengthλ = 6cm, Velocity v =120cm/sec and frequency n = v/λ= sec-1
The distance between adjacent nodes is λ/2 = 3cm.
Differentiating equation (i) with respect to t , we get
At x=1.5cm and t = 9/8sec, we have
Q.12. A string of mass 2.0gm/meter carries progressive waves of amplitude 1.5cm,
frequency 60sec-1 and speed 200meter / sec. Calculate the energy per meter length of the wire, and the rate of energy propagation in the wire.
The energy per meter length of the wire is given by, in usual notations,
Putting the given values:
E = 2 x (3.14)2 x (60 sec-1)2 x (1.5 x 10-2m)2 x (2.0 x 10-3kg/m)
= 3.2 x 10-2J/m
Rate of energy propagation = energy per unit length x wave speed
= 3.2 x 10-2Jm-1 x 200ms-1= 6.4W
Q.13. A wire of length 60.0cm and linear density 0.026 gm/cm3 is joined to another wire of length 86.6cm and linear density 3 0.078 gm/cm. It is stretched between two supports fixed in a horizontal line under a tension of 10 kg. Find the lowest frequency of an external source which would set up standing waves in the compound wire with a node at the joint, and the total number of loops in which the wire would vibrate at this frequency.
For the first wire; l = 60.0cm, m = 0.026gm/cm3, and T =10 x 1000 x 980 dynes.
Therefore, its natural frequencies are
For the second wire; l = 86.6cm, m = 0.078gm/cm and T =10x1000x980 dynes.Therefore, its natural frequencies areWhen the compound wire is excited, it would vibrate with a single frequency which must be one of the natural frequencies of both the individual wires if the standing waves are to be set up. We see from equation (i) and (ii) that the natural frequencies which is common to both wires is 323, which is second harmonic of the first wire and fifth harmonic of the second wire. With this frequency the first wire vibrates in 2 loops and the second one is 5 loops. Thus, required frequency of the external source = 323 and total number of loops in the compound wire = 2+5 = 7.
Q.14. In Melde’s experiment the string vibrates in 5 loops with a load of 20 gm. How much load will be required to make the string vibrate in 2 loops?
In Melde’s experiment the string vibrates with the fixed frequency n of the fork.
Hence if the length l is kept. If p T be the tension required to produce p loops, we have
Therefore, if T5 and T2 be the tensions to produce 5 and 2 loops respectively, we have
Here,
Q.15. A given 90cm long wire of sonometer is divided in three parts by two bridges whose fundamental frequencies are in the ratio 3: 4:6. Find the positions of the bridges.
By the law of length of stretched strings, we have
n1l1= n2l2=n3l3
Given that n1:n2:n3 = 3:4:6
The least common multiple is 12, so that we must have
l1:l2:l3 = 4:3:2The wire is 90cmlong. Hence to divide it in three parts in ratio 4:3: 2 , the bridges must
be placed at 40cm and 70 cm.
|
54 videos|22 docs|14 tests
|

|
Explore Courses for Physics exam
|

|
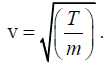
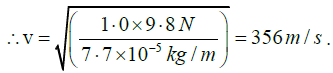
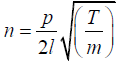
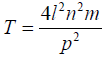
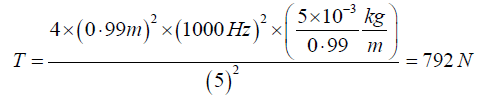
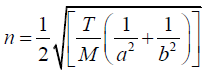
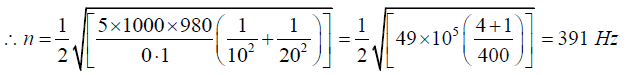
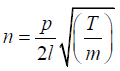 .... (1)
.... (1)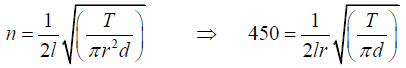 .....(2)
.....(2)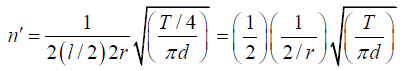
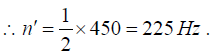
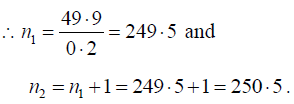
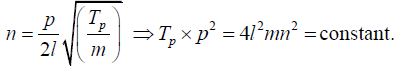
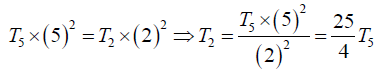
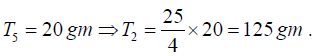
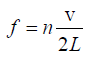 where, n =1,2,..............
where, n =1,2,..............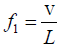
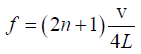 where, n =0,1,2,.............
where, n =0,1,2,.............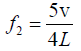
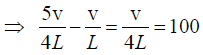

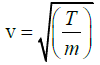
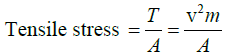
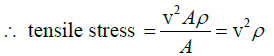
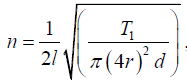 ...(1)
...(1)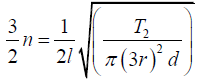 ...(2)
...(2)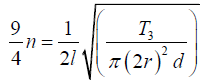 ....(3)
....(3)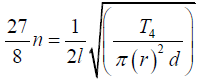 ... (4)
... (4)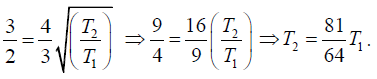
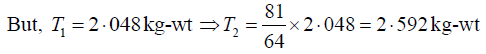
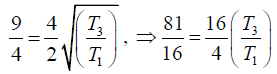
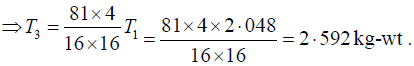
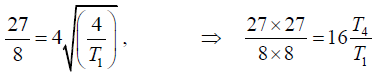
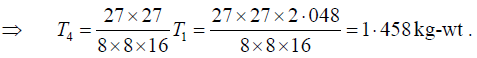
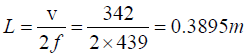
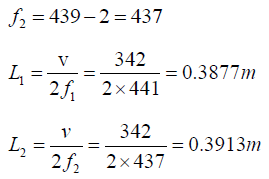
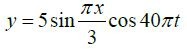 .....(1)
.....(1)