What are Quadratic Equations? | The Complete SAT Course - Class 10 PDF Download
| Table of contents |

|
| Introduction |

|
| Quadratic Formula Proof |

|
| Nature of Roots of the Quadratic Equation |

|
| Sum and Product of Roots of Quadratic Equation |

|
Introduction
- A quadratic equation is an algebraic equation of the second degree in x. The quadratic equation in its standard form is ax2 + bx + c = 0, where a and b are the coefficients, x is the variable, and c is the constant term. The first condition for an equation to be a quadratic equation is the coefficient of x2 is a non-zero term(a ≠ 0).
- For writing a quadratic equation in standard form, the x2 term is written first, followed by the x term, and finally, the constant term is written. The numeric values of a, b, c are generally not written as fractions or decimals but are written as integral values.
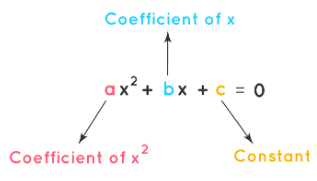
- Further in real math problems the quadratic equations are presented in different forms: (x - 1)(x + 2) = 0, -x2 = -3x + 1, 5x(x + 3) = 12x, x3 = x(x2 + x - 3). All of these equations need to be transformed into standard form of the quadratic equation before performing further operations.
Roots of a Quadratic Equation
- The roots of a quadratic equation are the two values of x, which are obtained by solving the quadratic equation. These roots of the quadratic equation are also called the zeros of the equation. For example, the roots of the equation x2 - 3x - 4 = 0 are x = -1 and x = 4 because each of them satisfy the equation. i.e.,
- At x = -1, (-1)2 - 3(-1) - 4 = 1 + 3 - 4 = 0
- At x = 4, (4)2 - 3(4) - 4 = 16 - 12 - 4 = 0
- There are various methods to find the roots of a quadratic equation. The usage of quadratic formula is one of them.
Quadratic Formula
- Quadratic Formula is the simplest way to find the roots of a quadratic equation. There are certain quadratic equations that cannot be easily factorized, and here we can conveniently use this quadratic formula to find the roots in the quickest possible way.
- The roots of the quadratic equation further help to find the sum of the roots and the product of the roots of the quadratic equation. The two roots in the quadratic formula are presented as a single expression. The positive sign and the negative sign can be alternatively used to obtain the two distinct roots of the equation.
Quadratic Formula: The roots of a quadratic equation ax2 + bx + c = 0 are given by x = [-b ± √(b2 - 4ac)]/2a.
Example: Let us find the roots of the same equation that was mentioned in the earlier section x2 - 3x - 4 = 0 using the quadratic formula.
a = 1, b = -3, and c = -4.
x = [-b ± √(b2 - 4ac)]/2a= [-(-3) ± √((-3)2 - 4(1)(-4))]/2(1)
= [3 ± √25] / 2
= [3 ± 5] / 2
= (3 + 5)/2 or (3 - 5)/2
= 8/2 or -2/2
= 4 or -1 are the roots.
Quadratic Formula Proof
- Consider an arbitrary quadratic equation: ax2 + bx + c = 0, a ≠ 0
- To determine the roots of this equation, we proceed as follows:
- ax2 + bx = -c ⇒ x2 + bx/a = -c/a
- Now, we express the left-hand side as a perfect square, by introducing a new term (b/2a)2 on both sides:
- x2 + bx/a + (b/2a)2 = -c/a + (b/2a)2
- The left hand side is now a perfect square:
- (x + b/2a)2 = -c/a + b2/4a2 ⇒ (x + b/2a)2 = (b2 - 4ac)/4a2
- This is good for us, because now we can take square roots to obtain:
- x + b/2a = ±√(b2 - 4ac)/2a
- x = (-b ± √(b2 - 4ac))/2a
- Thus, by completing the squares, we were able to isolate x and obtain the two roots of the equation.
Nature of Roots of the Quadratic Equation
- The roots of a quadratic equation are usually represented to by the symbols alpha (α), and beta (β). Here we shall learn more about how to find the nature of roots of a quadratic equation without actually finding the roots of the equation. And also check out the formulas to find the sum and the product of the roots of the equation.
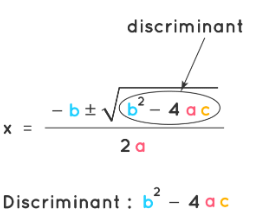
- The nature of roots of a quadratic equation can be found without actually finding the roots (α, β) of the equation. This is possible by taking the discriminant value, which is part of the formula to solve the quadratic equation. The value b2 - 4ac is called the discriminant of a quadratic equation and is designated as 'D'. Based on the discriminant value the nature of the roots of the quadratic equation can be predicted.
Discriminant: D = b2 - 4ac
- D > 0, the roots are real and distinct
- D = 0, the roots are real and equal.
- D < 0, the roots do not exist or the roots are imaginary.
Sum and Product of Roots of Quadratic Equation
- The coefficient of x2, x term, and the constant term of the quadratic equation ax2 + bx + c = 0 are useful in determining the sum and product of the roots of the quadratic equation. The sum and product of roots of a quadratic equation can be directly calculated from the equation, without actually finding the roots of the quadratic equation. The sum of the roots of the quadratic equation is equal to the negative of the coefficient of x divided by the coefficient of x2. The product of the root of the equation is equal to the constant term divided by the coefficient of the x2. For a quadratic equation ax2 + bx + c = 0, the sum and product of the roots are as follows.
- Sum of the Roots: α + β = -b/a = - Coefficient of x/ Coefficient of x2
- Product of the Roots: αβ = c/a = Constant term/ Coefficient of x2
- The quadratic equation can also be formed for the given roots of the equation. If α, β, are the roots of the quadratic equation, then the quadratic equation is as follows.
x2 - (α + β)x + αβ = 0
Formulas Related to Quadratic Equations
The following list of important formulas is helpful to solve quadratic equations.
- The quadratic equation in its standard form is ax2 + bx + c = 0
- The discriminant of the quadratic equation is D = b2 - 4ac
- For D > 0 the roots are real and distinct.
- For D = 0 the roots are real and equal.
- For D < 0 the real roots do not exist, or the roots are imaginary.
- The formula to find the roots of the quadratic equation is x = [-b ± √(b2 - 4ac)]/2a.
- The sum of the roots of a quadratic equation is α + β = -b/a.
- The product of the Root of the quadratic equation is αβ = c/a.
- The quadratic equation whose roots are α, β, is x2 - (α + β)x + αβ = 0.
- The condition for the quadratic equations a1x2 + b1x + c1 = 0, and a2x2 + b2x + c2 = 0 having the same roots is (a1b2 - a2b1) (b1c2 - b2c1) = (a2c1 - a1c2)2.
- When a > 0, the quadratic expression f(x) = ax2 + bx + c has a minimum value at x = -b/2a.
- When a < 0, the quadratic expression f(x) = ax2 + bx + c has a maximum value at x = -b/2a.
- The domain of any quadratic function is the set of all real numbers.
- For a > 0, the range of the quadratic function f(x) = ax2 + bx + c is [-(b2 - 4ac)/4a, ∞)
- For a < 0, the range of the quadratic function f(x) = ax2 + bx + c is : (-∞, -(b2 - 4ac)/4a]
Methods to Solve Quadratic Equations
- A quadratic equation can be solved to obtain two values of x or the two roots of the equation. There are four different methods to find the roots of the quadratic equation. The four methods of solving the quadratic equations are as follows.
- Factorizing of Quadratic Equation
- Using quadratic formula (which we have seen already)
- Method of Completing the Square
- Graphing Method to Find the Roots
Factorization of Quadratic Equation
- Factorization of quadratic equation follows a sequence of steps. For a general form of the quadratic equation ax2 + bx + c = 0, we need to first split the middle term into two terms, such that the product of the terms is equal to the constant term. Further, we can take the common terms from the available term, to finally obtain the required factors. For understanding factorization, the general form of the quadratic equation can be presented as follows.
- x2 + (a + b)x + ab = 0
- x2 + ax + bx + ab = 0
- x(x + a) + b(x + a)
- (x + a)(x + b) = 0
- Let us understand factorization through the below example.
- x2 + 5x + 6 = 0
- x2 + 2x + 3x + 6 = 0
- x(x + 2) + 3(x + 2) = 0
- (x + 2)(x + 3) = 0
- Thus the two obtained factors of the quadratic equation are (x + 2) and (x + 3). To find its roots, just set each factor to zero and solve for x. i.e., x + 2 = 0 and x + 3 = 0 which gives x = -2 and x = -3. Thus, x = -2 and x = -3 are the roots of x2 + 5x + 6 = 0.
- Further, there is another important method of solving a quadratic equation. The method of completing the square for a quadratic equation is also useful to find the roots of the equation.
Method of Completing the Square
- The method of completing the square in a quadratic equation is to algebraically square and simplify, to obtain the required roots of the equation. Consider a quadratic equation ax2 + bx + c = 0, a ≠ 0. To determine the roots of this equation, we simplify it as follows:
- ax2 + bx + c = 0
- ax2 + bx = -c
- x2 + bx/a = -c/a
- Now, we express the left hand side as a perfect square, by introducing a new term (b/2a)2 on both sides:
- x2 + bx/a + (b/2a)2 = -c/a + (b/2a)2
- (x + b/2a)2 = -c/a + b2/4a2
- (x + b/2a)2 = (b2 - 4ac)/4a2
- x + b/2a = ± √(b2- 4ac)/2a
- x = - b/2a ± √(b2- 4ac)/2a
- Now with this method of completing the square, we could consolidate the value for the roots of the equation. Further on simplification and taking the square root, the two possible roots of the quadratic equation are, x = (-b ± √(b2- 4ac))/2a. Here the '+' sign gives one root and the '-' sign gives another root of the quadratic equation. Generally, this detailed method is avoided, and only the quadratic formula is used to obtain the required roots.
Graphing a Quadratic Equation
- The graph of the quadratic equation ax2 + bx + c = 0 can be obtained by representing the quadratic equation as a function y = ax2 + bx + c. Further on solving and substituting values for x, we can obtain values of y, we can obtain numerous points. These points can be presented in the coordinate axis to obtain a parabola-shaped graph for the quadratic equation.
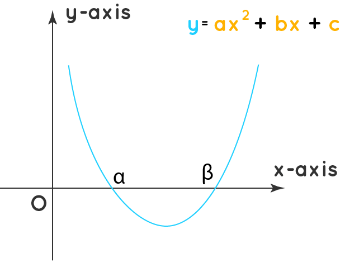
- The point(s) where the graph cuts the horizontal x-axis (typically the x-intercepts) is the solution of the quadratic equation. These points can also be algebraically obtained by equalizing the y value to 0 in the function y = ax2 + bx + c and solving for x.
Quadratic Equations Having Common Roots
- Let the two quadratic equations having common roots are a1x2 + b1x + c1 = 0, and a2x2 + b2x + c2 = 0. Let us solve these two equations to find the conditions for which these equations have a common root. The two equations are solved for x2 and x respectively.
- (x2)(b1c2 - b2c1) = (-x)/(a1c2 - a2c1) = 1/(a1b2 - a2b1)
- x2 = (b1c2 - b2c1) / (a1b2 - a2b1)
- x = (a2c1 - a1c2) / (a1b2 - a2b1)
- Hence, by simplifying the above two expressions we have the following condition for the two equations having the common root.
- (a1b2 - a2b1) (b1c2 - b2c1) = (a2c1 - a1c2)2
Maximum and Minimum Value of Quadratic Expression
- The maximum and minimum value for the quad equation F(x) = ax2 + bx + c = 0 can be observed in the below graphs. For positive values of a (a > 0), the quadratic expression has a minimum value at x = -b/2a, and for negative value of a (a < 0), the quadratic expression has a maximum value at x = -b/2a. x = -b/2a is the x-coordinate of the vertex of the parabola.
Maximum and Minimum Value of Quadratic Equation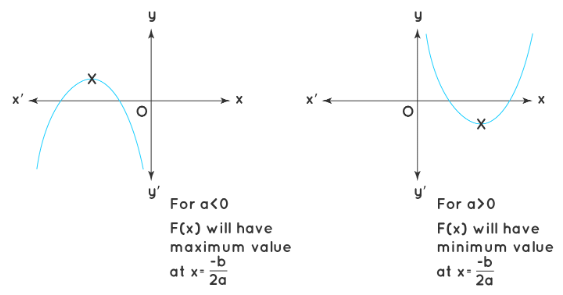
The maximum and minimum values of the quadratic expressions are of further help to find the range of the quadratic expression: The range of the quadratic expressions also depends on the value of a. For positive values of a( a > 0), the range is [ F(-b/2a), ∞), and for negative values of a ( a < 0), the range is (-∞, F(-b/2a)].
- For a > 0, Range: [ f(-b/2a), ∞)
- For a < 0, Range: (-∞, f(-b/2a)]
Note that the domain of a quadratic function is the set of all real numbers, i.e., (-∞, ∞).
Tips and Tricks on Quadratic Equation:
Some of the below-given tips and tricks on quadratic equations are helpful to more easily solve quadratic equations.
- The quadratic equations are generally solved through factorization. But in instances when it cannot be solved by factorization, the quadratic formula is used.
- The roots of a quadratic equation are also called the zeroes of the equation.
- For quadratic equations having negative discriminant values, the roots are represented by complex numbers.
- The sum and product of roots of a quadratic equation can be used to find higher algebraic expressions involving these roots.
|
433 videos|220 docs|166 tests
|
FAQs on What are Quadratic Equations? - The Complete SAT Course - Class 10
| 1. What is a quadratic equation? |  |
| 2. How do you solve a quadratic equation using the quadratic formula? |  |
| 3. Can a quadratic equation have no real solutions? |  |
| 4. What is the discriminant of a quadratic equation? |  |
| 5. How do you find the sum and product of the roots of a quadratic equation? |  |




















