What is Number Theory? | Mathematics for ACT PDF Download
Introduction
Number theory, also known as 'higher arithmetic', is one of the oldest branches of mathematics and is used to study the properties of positive integers. It helps to study the relationship between different types of numbers such as prime numbers, rational numbers, and algebraic integers.
In the mid-20s, the number theory was considered as one of the purest forms of mathematics until digital computers proved that this theory can provide answers to real-world problems.
Definition of Number Theory
The definition of number theory states that it is a branch of pure mathematics devoted to the study of natural numbers and integers. It is the study of the set of positive whole numbers usually called the set of natural numbers.
This theory is experimental and theoretical. While the experimental number theory leads to questions and suggests different ways to answer them, the theoretical number theory tries to provide a definite answer by solving it. Theoretically, numbers are classified into different types, such as natural numbers, whole numbers, complex numbers, and so on. Observe the following figure which shows the relationship between whole numbers, integers, and rational numbers.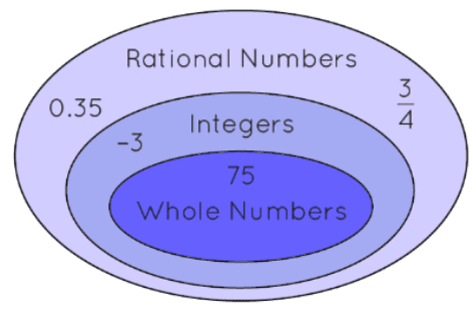
Number Theory Sub-classification
The numbers which are used in our day-to-day life can be classified into different categories. Here is a list that shows the subclassification of numbers:
- Odd Numbers
Odd numbers are those that are not divisible by the number 2. Numbers like 1, 3, 5, 7, 9, 11, 13, 15, and so on are considered as odd numbers. On the number line, 1 is considered as the first positive odd number. - Even Numbers
Even numbers are integers that are divisible by the number 2. For example, 2, 4, 6, 8, 10, 12, 14, 16, and so on are even numbers. - Square Numbers
Numbers that are multiplied by themselves are called square numbers or perfect square numbers. For example, in 3 × 3 = 9, 9 is a square number. Similarly, 1, 4, 9, 16, and so on are square numbers. - Cube Numbers
Numbers that are multiplied by themselves 3 times are called cube numbers. For example, 27 is a cube number because 3 × 3 × 3 = 27. Similarly, 1, 8, 64 are cube numbers. - Prime Numbers
Prime numbers are numbers that have only 2 factors, 1 and the number itself. For example, 3 is a prime number because it has only two factors, 1 and 3. In the same way, 2, 5, 7, 11 are prime numbers. - Composite Numbers
Unlike prime numbers that have only 2 factors, composite numbers are those that have more than 2 factors. In other words, composite numbers can be divisible by more than two numbers. For example, 6 is a composite number because it has more than two factors, that is, it is divisible by 1, 2, 3, and 6. - Fibonacci Numbers
A series of numbers where a number is the addition of the last two numbers, starting with 0 and 1 is known as the Fibonacci sequence. The numbers in this series or sequence are known as Fibonacci numbers. For example, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ..., is the Fibonacci sequence. Here, we can see that 1 + 1 = 2 , 1 + 2 = 3 , 2 + 3 = 5, 3 + 5 = 8 and so on.
Number Theory Uses
Number theory is used to find out if a given integer 'm' is divisible with the integer 'n' and this is used in many divisibility tests. This theory is not only used in Mathematics, but also applied in cryptography, device authentication, websites for e-commerce, coding, security systems, and many more.
Number Theory Examples
Example 1: Find the common factors of 12 and 18.
Solution: Factors of 12 = 1, 2, 3, 4, 6,12
Factors for 18 = 1, 2, 3, 6, 9,18
Therefore, the common factors are 1, 2, 3 and 6
Example 2: Find the Greatest Common Divisor (GCD) of the numbers 40 and 70.
Solution: Divisors (factors) of the number 40 are 1, 2, 4, 5, 8, 10, 20, 40.
Divisors (factors) of the number 70 are 1, 2, 5, 7, 10, 14, 35, 70.
The Greatest Common Divisor in 40 and 70 is 10.
Therefore, the GCD of 40 and 70 is 10.
|
144 videos|100 docs|61 tests
|
FAQs on What is Number Theory? - Mathematics for ACT
| 1. What is number theory? |  |
| 2. How is number theory useful in real life? |  |
| 3. What are prime numbers? |  |
| 4. What is modular arithmetic? |  |
| 5. What are Diophantine equations? |  |

|
Explore Courses for ACT exam
|

|

















