Word Problems: Area and Its Boundary | Mathematics for Class 5: NCERT PDF Download
Q1: Rina wants to lay tiles on her rectangular kitchen floor, which measures 5 meters by 3 meters. However, there is a square table of 1 meter side in the middle of the kitchen that will not be tiled. How much area of the kitchen floor will be tiled?
Sol: First, visualize the question statement.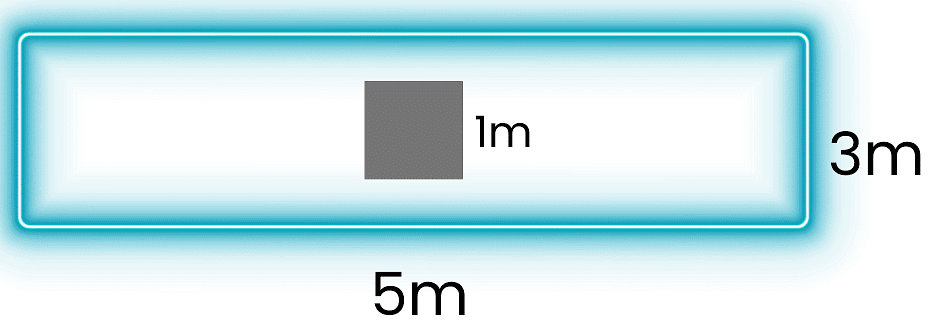 Calculate the area of the kitchen floor.
Calculate the area of the kitchen floor.
Area of the kitchen = Area of rectangle
= Length × Breadth
= 5 m × 3 m
= 15 square meters.
Now, Calculate the area of the table.
Area of the table = Area of a square
= Side × Side
= 1 m × 1 m
= 1 square meter.
Subtract the area of the table from the area of the kitchen.
Area to be tiled = Area of the kitchen - Area of the table
= 15 sq m - 1 sq m
= 14 square meters.
Rina will tile an area of 14 square meters.
Q2: A rectangular garden of length 15 m and breadth 13 m has to be fenced all around. What length of fencing will be required?
Sol: Length of fencing required = Perimeter of the rectangular garden
= 2( Length + Breadth)
= 2(15 m+ 13 m)
= 2 × 28 m
= 56 m
Q3: A rectangular garden is 20 meters long and 10 meters wide. A path of 2 meters wide runs around the outside of the garden. What is the area of this path?
Sol: Calculate the area of the garden without the path.
Area of the garden = Length × Width
= 20 m × 10 m
= 200 square meters.
Calculate the total area including the path.
Total length including path = 20 m + 2 m + 2 m
= 24 m (since the path is on both sides).
Total width including path = 10 m + 2 m + 2 m
= 14 m.
Total area including path = Total length × Total width
= 24 m × 14 m
= 336 square meters.
Area of the path = Total area including path - Area of the garden
= 336 sq m - 200 sq m
= 136 square meters.
The area of the path is 136 square meters.
Q4: Nehal is constructing a fence around her garden to prevent her favourite dog from escaping. What is the required fence length if the garden is 6 m broad and 9 m long? How much area does the dog have to run about in?
Sol:
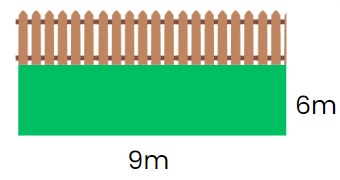 = Fence length required = Perimeter of the garden
= Fence length required = Perimeter of the garden
= 2(Length+Breadth)
= 2(6 m+ 9 m)
= 2 × 15 m
= 30 m
Now,
= Area of garden that dog have to run in = 6 m × 9 m
= 54 m²
Q5: A square pond has a side of 12 meters. Around the pond, there is a grassy border that is 3 meters wide. Calculate the total area covered by the grass.
Sol: Calculate the area of the pond.
Area of the pond = Side × Side
= 12 m × 12 m
= 144 square meters.
Calculate the total area including the grassy border.
Total side including border = 12 m + 3 m + 3 m
= 18 m (border on both sides).
Total area including border = Total side × Total side = 18 m × 18 m
= 324 square meters.
Area of the grass = Total area including border - Area of the pond = 324 sq m - 144 sq m
= 180 square meters.
The total area covered by the grass is 180 square meters.
Q6: Aman painted a wall that was 5 metres long and 4 metres wide. The door is no longer painted because it is 2 metres long and 1 metre broad. How big of an area must be painted?
Sol: Area of wall = length × breadth
= 5 m×4 m
= 20 m²
Area of door = length×breadth
= 2 m × 1 m
= 2 m²
Area painted = 20 m²-2m²
= 18 m²
Q7: A classroom's floor is completely covered with square tiles that each have a side length of 0.5 meters. The classroom is 8 meters long and 6 meters wide. How many tiles are there on the classroom floor?
Sol: Calculate the area of the classroom.
Area of the classroom = Length × Width
= 8 m × 6 m
= 48 square meters.
Calculate the area of one tile. Area of one tile = Side × Side
Area of one tile = Side × Side
= 0.5 m × 0.5 m
= 0.25 square meters.
Divide the area of the classroom by the area of one tile to find the number of tiles.
Number of tiles = Area of the classroom / Area of one tile
= 48 sq m / 0.25 sq m
= 192 tiles.
There are 192 tiles on the classroom floor.
Q8: Ralphy laid out a carpet that was 6 metres long and 4 metres wide in a room that was 5 metres long and 3 metres wide. How much area of carpet won't be used?
Sol: Area of Carpet = length×breadth
= 6 m × 4 m
= 24 m²
Area of room = length×breadth
= 5 m × 3 m
= 15 m²
Area of carpet that is not used = 24 m² - 15 m²
= 9 m²
Q9: Aman covered a square with wallpaper 6 m long side wall. The wall-mounted door, which is now 2 meters long and 1 meter wide, does not need to be covered. How much space needs to be wallpapered?
Sol: Area of square = (side)²
= (6 m)²
= 36 m²
Area of door = Length × Breadth
= 2 m× 1 m
= 2 m²
The area which should be covered with wallpaper = 36 m²-2m²
= 34 m²
Q10: In a square room with a side of 6 m, Raju laid a square carpet with a side of 4 m. How much floor space in the room will be left without carpet?
Sol: Area of square room = (side)²
= (6 m)²
= 36 m²
Side of carpet = 4 m
Area of square carpet = (4 m)²
= 16 m²
Area of floor space left which is not carpeted = 36m²-16m²
= 20 m².
|
31 videos|192 docs|41 tests
|
FAQs on Word Problems: Area and Its Boundary - Mathematics for Class 5: NCERT
| 1. What is the formula for finding the area of a rectangle? |  |
| 2. How do you find the perimeter of a square? |  |
| 3. What is the difference between area and perimeter? |  |
| 4. How do you find the area of a triangle? |  |
| 5. Can the area of a shape be greater than its perimeter? |  |
















