Work and Energy in Electrostatics | Electricity & Magnetism - Physics PDF Download
In an external field E, the work done in moving a test charge Q, from a to b is,
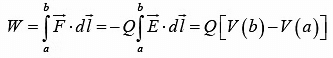
If a =∞ and b =r
⇒ W=Q[V(r) −V(∞)] = QV (r ) since V(∞) = 0 The potential energy (the work it takes to create the system) per unit charge
(just as the field is the force per unit charge).
The potential energy (the work it takes to create the system) per unit charge
(just as the field is the force per unit charge).
Energy of Point Charge Distribution
When the first charge q1 is placed, no work has been done. When q2 is placed work done W2 =q2V1 where V1 is the potential due to q1 so,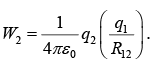
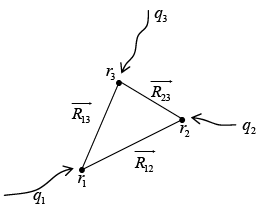
Similarly when the third charge q3 is placed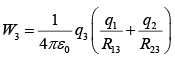
The work necessary to assemble the first three charges is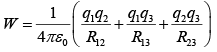
In general,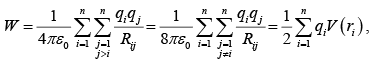
where V(ri) is the potential at point ri (the position of qi ) due to all other charges.
Example 1: Four charges are situated at the corners of a square (side a ) as shown in the figure. How much work does it take to assemble the whole configuration of four charges?
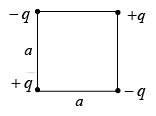
Solution: Work done in placing first charge ( −q charge upper left corner) W1 = 0
Work done in placing second charge ( + q charge lower left corner)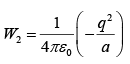
Work done in placing third charge ( −q charge lower right corner)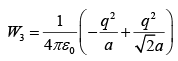
Potential at the fourth corner ( +q charge upper right corner)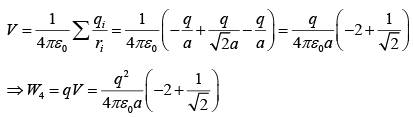
Total work done =W1+W2 +W3 +W4 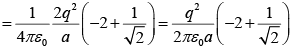
Example 2: Three charges are arranged in an equilateral triangle of side length a. Calculate the total work done in assembling this configuration of charges.
Solution:
To calculate the total work done in assembling this configuration of charges, we need to consider the work done in bringing each charge from infinity to its final position in the equilateral triangle. Let the charges be q, q, and q, and the side length of the equilateral triangle be a. The work done in bringing the first charge from infinity to its position in the triangle is zero, as there are no other charges present initially. Now, let's consider the work done in bringing the second charge to its position. The electric potential energy of the second charge at its final position in the presence of the first charge is given by: 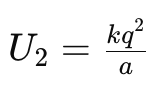 where k is the Coulomb's constant.
where k is the Coulomb's constant.
The work done in bringing the second charge from infinity to its final position is the change in its potential energy, which is:
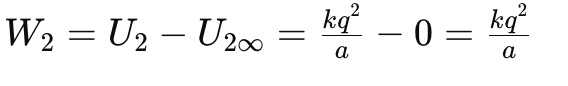
Next, let's consider the work done in bringing the third charge to its position. The electric potential energy of the third charge at its final position in the presence of the first two charges is given by:
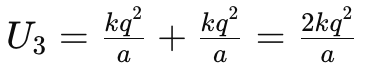
The work done in bringing the third charge from infinity to its final position is the change in its potential energy, which is:
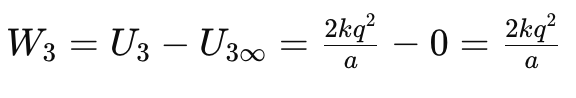
Therefore, the total work done in assembling this configuration of charges is:
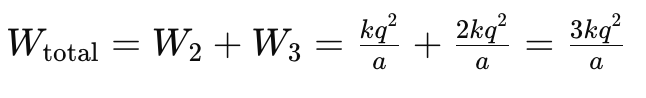
So, the total work done in assembling this configuration of charges is 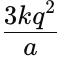
The Energy of Continuous Charge Distribution
For a volume charge density
Since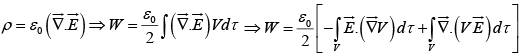
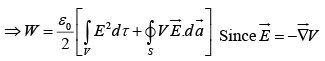
The above equation gives the correct energy W, whatever volume we use as long as it encloses all the charges, but the contribution from the volume integral goes up, and that of the surface integral goes down, as we take larger and larger volumes. In particular, if we integrate over all space, then the surface integral goes to zero, and we have

Example 3: Energy of a uniformly charged spherical shell of total charge q and radius R.
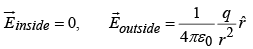
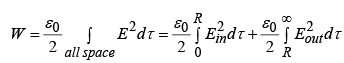
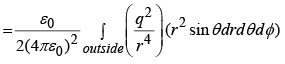
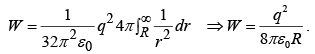
Example 4: Find the energy stored in a uniformly charged solid sphere of radius R and charge q.
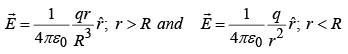
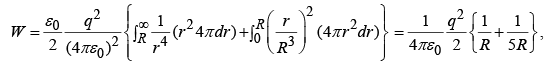
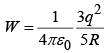
|
82 videos|29 docs|22 tests
|




















