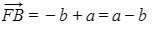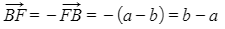Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Working with Vectors
Working with Vectors | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Finding Vector Paths
Finding paths in vector diagrams
- Understanding vectors often involves tracing paths through geometric diagrams.
- In the provided grid, comprised entirely of parallelograms, vectors a and b are identified as shown.
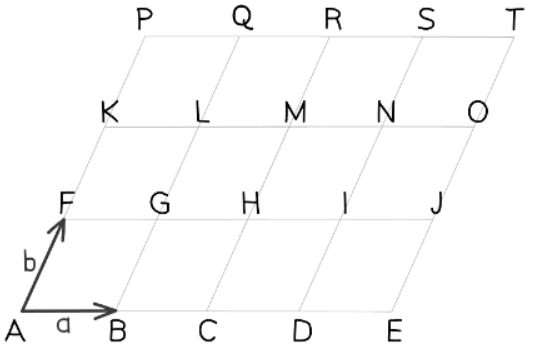
- Note the difference between "specific" and "general" vectors
- The vector stack
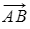 in the diagram is specific and refers only to the vector starting at A and ending at B
in the diagram is specific and refers only to the vector starting at A and ending at B - However, the vector a is a general vector - any vector the same length as stack
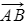 and pointing in the same direction is equal to a
and pointing in the same direction is equal to a - Similarly, any vector the same length as
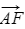 and pointing in the same direction is equal to b
and pointing in the same direction is equal to b
- The vector stack
- Following a vector in the "wrong" direction (i.e. from head to tail instead of from tail to head) makes a general vector negative
- So in the diagram above stack
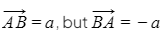
- Similarly
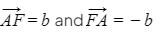
- So in the diagram above stack
- Note in particular the vector
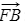 :
:
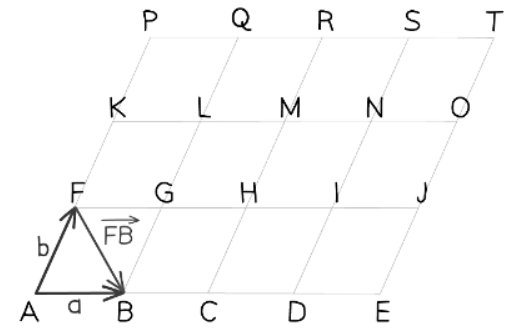
- Getting from point to point we have to go the 'wrong way' down and then the 'right way' along
- It follows that:
- and of course then
- Keeping those things in mind, it is possible to describe any vector that goes from one point to another in the above diagram in terms of a and b
Vector Problem Solving
What are vector proofs?
- Vector proofs entail employing vectors, coupled with key concepts, to establish the validity of geometric assertions within diagrams.
- Problem-solving with vectors encompasses leveraging these vector proofs to deduce supplementary information and address challenges effectively.
Parallel vectors
- Two vectors are parallel if and only if one is a scalar multiple of the other.
- This principle manifests in vector proofs in the following ways:
- If during your calculations you determine that one vector is a scalar multiple of the other, then you can conclude that the two vectors are parallel. This established fact can then be utilized in subsequent parts of the proof.
- To demonstrate that two vectors are parallel, it suffices to show that one of the vectors, when multiplied by a scalar, equals the other vector.
- For instance:
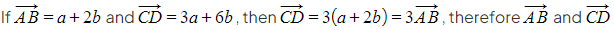 are parallel
are parallel
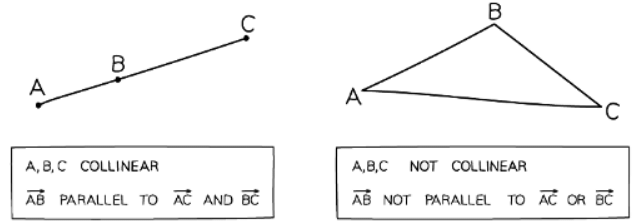
Points on a straight line
- Often you are asked to show in a vector proof that three points lie on a straight line (ie that they are collinear)
- To show that three points A, B and C lie on a straight line,
- show that the vectors connecting the three points are parallel,
- for example, show that stack
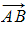 is a multiple of (and therefore parallel to) stack
is a multiple of (and therefore parallel to) stack  is a multiple of (and therefore parallel) to
is a multiple of (and therefore parallel) to 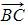
- for example, show that stack
- as those two vectors are parallel and they share a common point it means that the three lines form a straight line
- show that the vectors connecting the three points are parallel,
Vectors divided in ratios
- Be careful turning ratios into fractions in vector proofs!
- If a point divides a line segment in the ratio p : q, then:
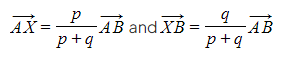
- eg. In the following diagram, the point divides in the ratio 3 : 5:
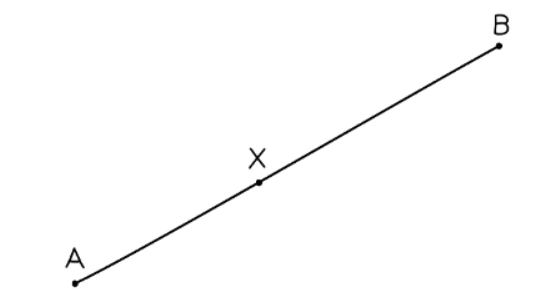
Therefore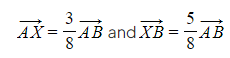
The document Working with Vectors | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
66 videos|674 docs|19 tests
|
FAQs on Working with Vectors - Mathematics for GCSE/IGCSE - Class 10
| 1. What is the difference between specific and general vectors? |  |
Ans. Specific vectors have fixed magnitudes and directions, while general vectors can be represented by variables and can vary in magnitude and direction.
| 2. How can vectors be expressed in terms of a and b? |  |
Ans. Vectors can be expressed as a linear combination of a and b, where a and b are scalar constants multiplied by the unit vectors i and j, respectively.
| 3. How can vectors be used to solve problems in mathematics? |  |
Ans. Vectors can be used to solve problems involving displacement, velocity, force, and more by representing quantities with magnitude and direction.
| 4. What does it mean for points to be on parallel vectors? |  |
Ans. Points that lie on parallel vectors have the same direction but may have different magnitudes, indicating a relationship in their paths or movements.
| 5. How can vectors be applied in geometry concepts? |  |
Ans. Vectors can be used to determine distances, angles, and relationships between points in geometric shapes, providing a mathematical framework for analyzing spatial relationships.
Related Searches