Area and its Boundary - 2 Class 5 Worksheet Maths Chapter 11
Q1: Fill in the blanks.
(i) The perimeter of a square with side 3 cm is ______.
Ans: 12 cm
(ii) Area of a rectangle 5 cm long and 3 cm width is ______ sq cm.
Ans: 15 sq cm
(iii) Area of a square is ______.
Ans: Side x side
(iv) The length of the boundary is known as ______.
Ans: Perimeter
(v) The perimeter of a triangle of sides 4 cm, 3 cm and 2 cm is ______.
Ans: 9 cm
Q2: Answer the following Questions.
(i) Perimeter of a square is 48 cm. Find the length of its side?
Ans: Perimeter = 48 cm
Length of a side = perimeter/4 = 48/4 =12cm
(ii) The length of a rectangular garden is 20 m and breadth is 13 m. How much barbed wire will be needed to fence the garden?
Ans: Given l = 20 m, b = 13 m
Perimeter = 2 x (l + b) = 2 x (20 + 13) = 2 x 33 = 66 m
(iii) Find the area of a rectangle whose length is 12 cm and breadth is 10 cm.
Ans: Given l=12 cm, b= 10 cm
Area = l x b = 12 x 10 = 120 sq cm
(iv) A square garden has a perimeter 40m. What is its area?
Ans: Given perimeter = 40 m
Length of a side = perimeter/ 4 = 40 / 4 = 10 m
Area = side x side = 10 x 10 = 100 sq m
(v) A rectangular field is 24 m long and 20 m wide. Find the cost of fencing the field at the rate of 25 rupees per metre.
Ans: Given l= 24 m, b = 20 m
Perimeter = 2 x (l + b) = 2 x (24 + 20) = 2 x 44 = 88 m
Cost of fencing = 88 x 25 = 2200 rupees.
(vi) The fencing of a square garden is 32 m in length. How long is one side of the garden?
Ans: Given perimeter = 32 m
Length of one side = 32/ 4 = 8m
(vii) A thin wire 40 cm long is formed into a rectangle. If the width of this rectangle is 8 cm, what is its length?
Ans: Perimeter =2 x (l + b) = 40 cm and b = 8 cm
l + b = 20
l + 8 = 20
l = 20 – 8 = 12cm
(viii) Find the perimeter of a triangle with sides measuring 10 cm, 14 cm and 15 cm?
Ans: Perimeter = 10 + 14 + 15 = 39 cm
(ix) Find the side of the square whose perimeter is 20m?
Ans: Length of the side of a square = perimeter / 4 = 20/4 = 5 m
(x) The area of a rectangular garden 50 m long is 300 sq m. Find the width of the garden?
Ans:
Given l = 50 m
Area = 300 sq m
Width = Area/ length = 300/ 50 = 6 m
(xi) Find the area of a square whose perimeter is 100 cm. Ans: We know that the sides of a square are equal and a square has four sides.
Ans: We know that the sides of a square are equal and a square has four sides.
So, side of the square = 100 / 4 = 25 cm
Area of square = s x s = 25 x 25 = 625 square cm.
(xii) Find the area of a square whose perimeter is 64 m.
Ans: We know that the sides of a square are equal and a square has four sides.
So, side of the square = 64 / 4 = 16 m
Area of square = s x s = 16 x 16 = 256 square cm.
(xiii) Find the area of a rectangle whose perimeter is 100 cm and length is 20cm. Ans: Perimeter = 100 cm Length= 30 cm
Ans: Perimeter = 100 cm Length= 30 cm
We know that the opposite sides of a rectangle are equal and a rectangle has four sides.
So, width of the rectangle = 100- (30 + 30) divided by 2
= 40/2 = 20 cm
Now, area of rectangle = l x b = 30 x 20 = 600 square cm.
(xiv) Find the area of a rectangle whose perimeter is 50 m and width 10 cm. Ans: Perimeter = 50 m Width= 10 m
Ans: Perimeter = 50 m Width= 10 m
We know that the opposite sides of a rectangle are equal and a rectangle has four sides.
So, length of the rectangle = 50- (10 + 10) divided by 2
= 30/2 = 15 m
Now, area of rectangle = l x b = 15 x 10 = 150 square m.
(xv) Compare the areas of a square with side 6 cm and rectangle (length= 6 cm and width = 5 cm).
 Ans: Area of square
Ans: Area of square
Side x side
6 cm x 6 cm = 36 cm sq.
And
Area of square with side 6 cm
Length x width
6 cm x 5 cm = 30 cm sq.
Area of Square > Area of Rectangle
(xvi) Compare the areas of these rectangles A and B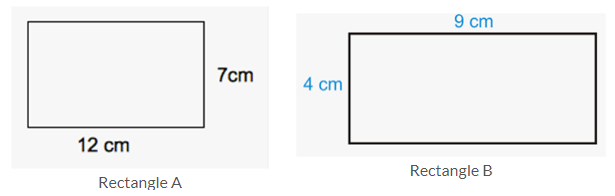 Ans: Area of rectangle A
Ans: Area of rectangle A
Length x width
12 cm x 7 cm = 84 cm sq.
And,
Area of rectangle B
Length x width
9 cm x 4 cm = 36 cm sq.
Area of rectangle A > Area of rectangle B
(xvii) Compare the area of a square with side 5 cm and another square with side 6 cm.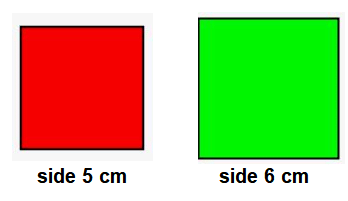 Ans: Area of square with side 5 cm
Ans: Area of square with side 5 cm
Side x side
5 cm x 5 cm
= 25 cm sq.
And,
Area of square with side 6 cm
Side x side
6 cm x 6 cm
= 36 cm sq.
Area of square with side 5 cm < Area of square with side 6 cm
(xviii) Compare the areas of the following figures.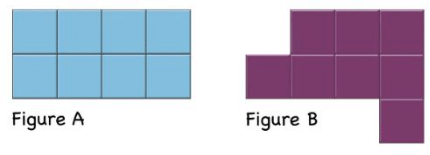 Ans: There are 8 unit squares in Figure A.
Ans: There are 8 unit squares in Figure A.
There are 8 unit squares in Figure B also.
So, the area of figure A and figure B are the same.
|
31 videos|286 docs|45 tests
|
FAQs on Area and its Boundary - 2 Class 5 Worksheet Maths Chapter 11
| 1. What is the definition of area in mathematics? |  |
| 2. How is the area of a rectangle calculated? |  |
| 3. What is the formula to find the area of a circle? |  |
| 4. How can we find the area of an irregular shape? |  |
| 5. What is the difference between perimeter and area? |  |
















