Basic Geometrical Ideas Class 6 Worksheet Maths Chapter 4
Q1: What do the following things in our surroundings represent: (use the words given in the box).
| A point | A ray | A line segment |
| A plane | Parallel lines | Intersecting lines |
Tip of pencil A point (example)
(a) Edge of a ruler __________
(b) Corner of a book __________
(c) Light coming out of torch __________
(d) Flat surface of a table __________
(e) Opposite edges of a ruler __________
(f) Adjacent edges of a ruler __________

Ans: Basic Geometrical Ideas
(a) Line segment
(b) Point
(c) Ray
(d) Plane
(e) Parallel lines
(f) Intersecting lines
Q2: In relation to the adjoining figures, write the names of: 
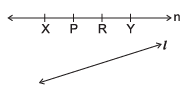
(a) 6 line segments
(b) 6 rays
(c) Two intersecting lines
(d) Two parallel lines
(e) How many points have been marked and named on the line 'n'?
(f) How many lines can pass through a single point?
Ans: (a) Line segments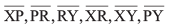
(b) Rays 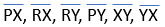
(c) Line 'n' and line 'l'
(d) line 'm' and line 'n'
(e) 4
(f) Infinitely many
Q3: What is the name of the angle shown in this figure? Name the points.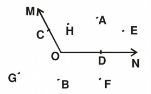 (a) In the interior of the angle
(a) In the interior of the angle
(b) On the angle
(c) In the exterior of the angle.
Ans: ∠MON
(a) Points in the interior of the angle are: A, H, E
(b) Points on the angle are: C, D
(c) Points in the exterior of the angle are: G, B, F
Q4: State whether the following statements are true or false:
(a) A line segment is a definite part of a line.
Ans: True
A line segment has two endpoints, which make it a specific, measurable part of a line.
(b) Through a given point, only one line can be drawn.
Ans: False
You can draw infinitely many lines through a point.
(c) A line is not a curve.
Ans: True
In geometry, a line is defined as a straight path that extends infinitely in both directions, unlike curves which deviate from this straightness.
(d) The interior of an angle is a restricted area.
Ans: False
The interior of an angle is not restricted; it simply refers to the space between the two arms of the angle.
(e) Line is a part of a ray.
Ans: False
A ray is a part of a line that starts from one point and goes on infinitely in one direction, but a line is infinite in both directions.
(f) Two lines in a plane can intersect each other at two points.
Ans: False
Two lines in a plane can intersect at only one point, not two.
Q5: Which of the following are polygons:-
(a) 
(b)
(c)
(d)
(e)
Ans: (a), (e) are polygons.
Q6: Match the following:
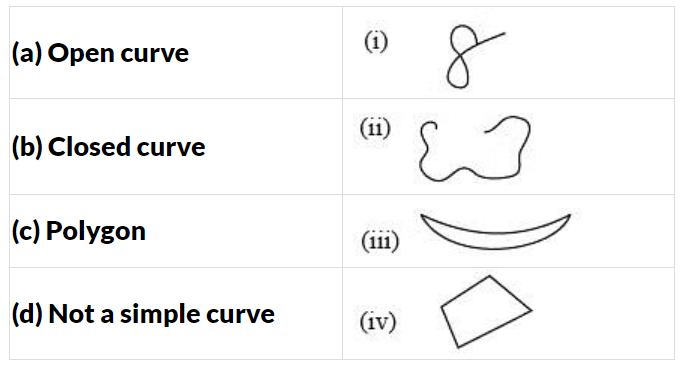
Ans:
(a) ↔ (ii),
(b) ↔ (iii),
(c) ↔ (iv),
(d) ↔ (i)
Q7: Name the rays in this figure. How many angles are being formed?
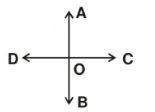 Ans: A ray begins at a point and extends infinitely in one direction. In the given figure:
Ans: A ray begins at a point and extends infinitely in one direction. In the given figure:
OA, OB, OC, and OD are the rays.
The angles formed by these rays are ∠AOB, ∠BOC, ∠COD, and ∠DOA. Therefore, a total of 4 angles are formed.
Q8: Identify and name the pairs of parallel lines.
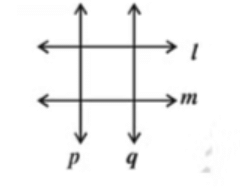
Ans: Parallel lines are lines in a plane that do not meet; they are always the same distance apart. In the figure:
The pairs of parallel lines are lm and p ∥ q.
Q9: Identify the points which are:
(a) In the exterior of the curve
(b) On the curve
(c) In the interior of the curve
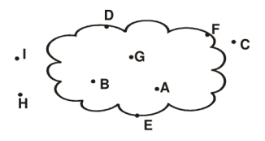
Ans.
(a) In the exterior of the curve: Points C, H and I are in the exterior of the curve.
(b) On the curve: Points D, E, and F are on the curve.
(c) In the interior of the curve: Points A, B, and G are in the interior of the curve.
Q10: 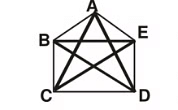
(a) Name the 5 vertices forming this figure.
Ans: The five vertices forming this figure are A, B, C, D, and E.
(b) Name any 2 adjacent sides.
Ans: Adjacent sides share a common vertex. Two examples of adjacent sides in this figure are AB and BC.
(c) Name any 2 opposite sides.
Ans: Opposite sides do not share a common vertex and are across from each other. Two examples of opposite sides in this figure are BC and ED.
(d) Name the diagonals.
Ans: Diagonals are line segments that connect non-adjacent vertices. The diagonals in this figure are AC, AD, BD, BE, and CE.
FAQs on Basic Geometrical Ideas Class 6 Worksheet Maths Chapter 4
| 1. What are the basic geometrical shapes that we study in Class 6? |  |
| 2. How can I calculate the perimeter of a shape? |  |
| 3. What is the difference between a line and a line segment? |  |
| 4. Can you explain the types of angles we learn in Class 6? |  |
| 5. What is the importance of understanding symmetry in geometry? |  |






















