Class 5 Maths - How Many Squares - CBSE Worksheets Solutions - 1
Q1: Fill in the blanks.
(i) A square with 1 cm length will have an area of ______
Ans: 1 square cm
(ii) Area of a square with side 2 m is ______ square metres.
Ans: 4 square meters
(iii) Length of a boundary is called ______
Ans: Perimeter
(iv) Measure of the space enclosed in a plane figure is called ______
Ans: Area
Q2: Answer the following Questions.
(i) Draw 2 straight lines in this rectangle to divide it into 1 rectangle and 2 equal triangles. Find the area of the new rectangle and the area of 1 of the triangles.
Ans:

Total number of squares in the rectangle = 8
Number of squares covered in rectangle = 2
So, area of rectangle = 2 squares
Number of squares covered in both the triangles = 6
Hence, number of squares covered in 1 triangle = 3
So, area of triangle = 3 squares
(ii) Write the area in square cm of the shaded portion.
 Ans: Total number of squares in the given figure = 16
Ans: Total number of squares in the given figure = 16
The shaded portion is half of the given figure.
So the area of the shaded portion = 8 square cm
(iii) Find the perimeter and area of the following figure.
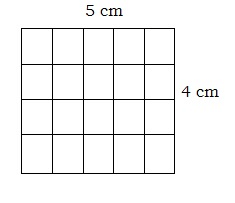 Ans: The perimeter is the length of the boundary.
Ans: The perimeter is the length of the boundary.
So perimeter = 5 + 4 + 4 + 4 = 18 cm
Area = Total number of squares = 20 square cm
(iv) Look at the following image: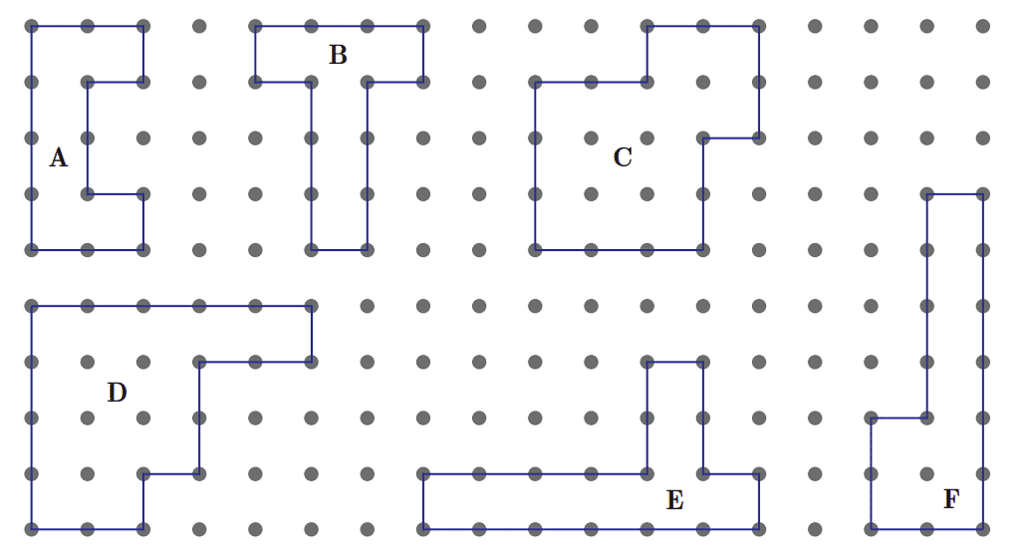
(a) Which shape has the maximum perimeter? Its perimeter is ______ cm.
Ans: Shape D has the maximum perimeter
Its perimeter is 18 cm.
The perimeter is calculated by counting the number of dots on boundary.
(b) Which shape has the minimum perimeter? Its perimeter is ______ cm.
Ans: Shape A has the minimum perimeter
Its perimeter is 14 cm.
(c) The perimeter of figure D is ____ cm. It is _____ (less/more) than the perimeter of figure A which is______ cm.
Ans: The perimeter of D is 18 cm.
It is more than the perimeter of A, which is 14 cm.
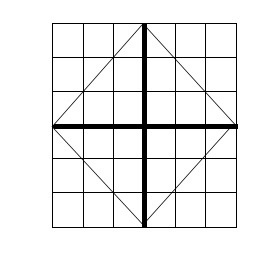
(v) Study the diagram given below. Draw 2 more lines so that the area is 18 square cm.
 Ans: Consider the given square as four equal squares.
Ans: Consider the given square as four equal squares.
The first line is half of the first square.
So its area is 4.5 square cm (half of 9 squares).
Similarly, the area of the second square also 4.5 square cm.
So total area is 9 square cm.
So to get 18 square cm area we can draw two lines as the same pattern as given in the figure. This is given as follows:
(vi) Here is a rectangle of an area of 20 square cm. Answer the following based on this:
(a) Draw one straight line in this rectangle to divide it into two equal triangles. What is the area of each of the triangles?
Ans: Area of each triangle = ½ X area of a rectangle
= ½ X 20 = 10 square cm
(b) Draw one straight line in this rectangle to divide it into two equal rectangles. What is the area of each of the smaller rectangles?
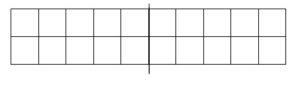 Ans: Area of each smaller rectangle = ½ area of the bigger rectangle
Ans: Area of each smaller rectangle = ½ area of the bigger rectangle
= ½ X 20 = 10 square cm
(vii) Answer the following questions:
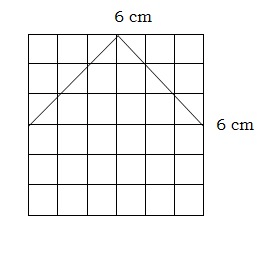
(a) The area of a square is 9 cm. Find the area of shaded part: Ans: Area of the square = 9 cm
Ans: Area of the square = 9 cm
The shaded part is half of the square
So the area of the shaded part = Area of square/ 2
9/2 = 4.5 sq. cm
(b) Find the perimeter of the following figure: Ans: Perimeter = Sum of all sides
Ans: Perimeter = Sum of all sides
So, 2 + 4 + 2 + 4 = 12 cm
(c) Find the area of the shaded shape: Ans: The shaded shape includes 5 squares and 2 triangles
Ans: The shaded shape includes 5 squares and 2 triangles
Area of 1 square = 1 cm
Area of triangle = Area of square/2
Area of 2 triangles = 1/2 + 1/2 = 1
Total area = 5 +1 = 6 sq. cm
(d) Find the area of the following: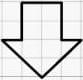
Ans: The shaded shape includes 6 squares and 4 triangles
Area of 1 square = 1 cm
Area of 6 squares = 6 cm
Area of triangle = Area of square/2
Area of 4 triangles = 1/2 + 1/2 + 1/2 + 1/2 = 2
Total area = 6 +2 = 8 sq.cm
(e) Find the area of the shaded path.
Ans: The shaded path includes 12 squares and 8 triangles
Area of 1 square = 1 cm
Area of 12 squares = 12 cm
Area of triangle = Area of square/2
Area of 8 triangles = 1/2 + 1/2 + 1/2 + 1/2 + 1/2 + 1/2 + 1/2 + 1/2 = 4
Total area = 12 +4 = 16 sq.cm
(vii) Find the perimeter and area of the figure by counting the squares. Ans: Perimeter = 12 cm
Ans: Perimeter = 12 cm
(viii) Draw your own tile pattern using triangles.
Ans: 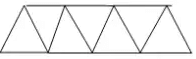
(ix) Draw one straight line in the following rectangle to divide it into two equal triangles. What is the area of each of the triangles?
Ans: 
Total number of squares = 20
Area of each triangles = 10 squares.
(x) Draw lines and divide the figure into parts having equal area as two triangles. Ans:
Ans: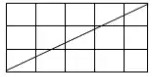
|
28 videos|169 docs|41 tests
|
FAQs on Class 5 Maths - How Many Squares - CBSE Worksheets Solutions - 1
| 1. What is the method to calculate the number of squares in a grid? |  |
| 2. How can I find the number of squares in a rectangle? |  |
| 3. Are there different types of squares I should consider in a grid? |  |
| 4. Can I use a visual method to count the squares instead of a formula? |  |
| 5. What are some common mistakes to avoid when counting squares? |  |

|
Explore Courses for Class 5 exam
|

|


















