X-Ray Diffraction | Solid State Physics, Devices & Electronics PDF Download
X-Ray diffraction
Structure Factor
The atomic scattering factor or form factor f describes the scattering power of a single atom in relation to the scattering power of a single electron and given by:
f = amplitude of radiation scattered from an atom/amplitude of radiation scattered from an electron
In general f < Z, it approaches Z (atomic no.) in the limit case. The phase difference between the wave scattered from the charge ρ(r) dv and that scattering from electron, in accordance equation is given by
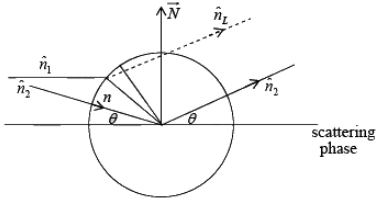
➤ Geometric Structure Factor
The intensity of an x-ray beam diffracted from a crystal not only depends upon the atomic scattering factor of the various atom involved but also on the contents of the unit cell, i.e. on the number. The total scattering amplitude F(h' k' l') for the reflection (h' k' l') is defined as the ratio of the amplitude of radiation scattered by a single point electron placed at origin for the same wavelength. It is given by: 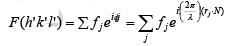
where fj is the atomic scattering factor for the jth atom αφj is the phase difference if (uj, vj, wj) represents the co-ordinate of jth atom we can write rj = uja + vjb +wjc, and
rj .N = λ (ujh + vjk + wjl) 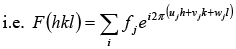
For identical atoms, all the fj’s have the same value f. Therefore, equation (i) take a simple form. F(hkl) = f S
where = 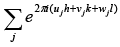 is called Geometrical Structure Factor.
is called Geometrical Structure Factor.
Now since the intensity of a radiation is proportional to the square of its amplitude, the intensity of diffracted beam may be written by I = |F|2 = F* F
The structure factor for some simple crystals are calculated below and the intensity of various order of reflections associated with these structures is discussed.
Note: (i) We can by find the structure factor allowed reflection by given crystal structure either wise zero.
(ii) eiθ = cos θ + i sin θ or eiπ = cos π + i sin π
(a) Simple cubic crystal: Unit cell contains only one atom at the origin
i.e. (u, v, w) = (0, 0, 0)
∴ F = fe2πi(0) = f
And therefore intensity which is the square of the amplitude is F2 = f2.
Thus F2 is thus independent of h, k & l and the same for all reflection.
∴ All h, k, l are possible in SC.
(b) Base centered cell: It has 2 atoms at 0, 0, 0 & 1/2, 1/2, 0
∴ F = f[1 + eπi(h + k)]
And F = 2f ⇒ F2 = 4f2: for h & k unmixed
While F = 0 ⇒ F2 = 0: for h & k mixed
Note : The value of l index has no effect on the structure factor
∴ Present planes are: (111), (112), (113) & (021), (022), (023)
Absent planes are: (011), (012), (013) & (101), (102), (103)
(c) Body Centered cell: It has 2 atoms at (0 0 0) & (1/2 1/2 1/2)
∴ F = f[1 + eπi(h + k + l)]
And F = 2f ⇒ F2 = 4f2: when (h + k + l) = Even
While F = 0 ⇒ F2 = 0: when (h + k + l) = odd
∴ Present planes are: (1 1 0), (2 0 0), (2 2 2) etc
Absent planes are: (1 0 0), (1 1 1), (2 1 0) etc
(d) Face centered cell: It has 4 atoms at (0 0 0), 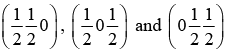
∴ F = f [1 + eπi(h + k) + eπi(h + l) + eπi(k + l)]
And F = 4f ⇒ F2 = 16f2 : If h, k, l are unmixed
While F = 0 ⇒ F2 = 0 : If h, k, l are mixed
∴ Present planes are: (1 1 1), (2 0 0), (2 2 0) etc
Absent planes are: (1 0 0), (1 1 0), (2 1 1) etc.
➤ Simplified Table

Note: (1) The first order reflection from (1 0 0) planes in a bcc crystal is absent, while second order reflections from (1 0 0) plane is present and it is this reflection which appears at the position of the 1st order reflection from (2 0 0) planes.
(2) The ratio of (h2 + k2 + l2) values for all allowed reflection from cubic crystal as obtained from the extinction rules are given as follows. 
Braggs Law
X-rays are a form of electromagnetic radiation and these are used for determining the crystal structures are they have high energy and short wavelengths. The wavelengths of x-rays are of the order of the atomic spacing for solids. When a beam of x-rays impinges on a solid material, a portion of this beam will be scattered in all direction by the electrons associated with each atom or ion that lies within the beam path.
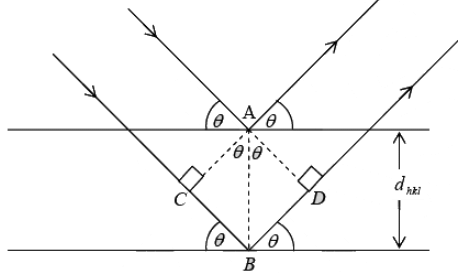
From figure n λ = CB + BD
In ∆ ABC,
CB = AB sin θ = dhkl sin θ
BD = AD sin θ = dhkl sin θ
∴ dhkl sinθ = nλ
2dhkl sin θ = nλ
This is known as Bragg’s law, n is order of reflection. For SC a = b = c 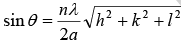
Methods of X-ray Diffraction
In x-ray diffraction studies, the probability that the atomic planes with right orientations are exposed to x-rays is increased by adopting there of crystal structure studies method.
(1) Law Method
(2) Rotating Method
(3) Powder Method
(1) Laue’s Technique:- The single crystal is held stationary and a beam of white radiations is inclined on it at a fixed glacing angle θ i.e. θ is fixed while λ is varies different wavelengths present in the white radiations select the appropriate reflecting planes out of the numerous present in the crystal such that the Bragg’s condition is satisfied this technique is called the Laue’s technique.
(2) Rotating Crystal Method:- A single crystal is held in the path of monochromatic radiations and is rotated about an axis i.e. λ is fixed while θ varies. Different sets of parallel atomic planes are exposed to incident radiations for different values of θ and reflections take place from those atomic planes for which d and θ satisfied the Bragg’s law. This method is known as the rotating crystal method.
(3) Powder Method:- Modern x-ray crystal analysis uses an x-ray diffractometer which has a radiation counter to detect the angle and intensity of the diffraction beam.
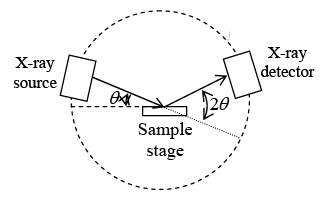
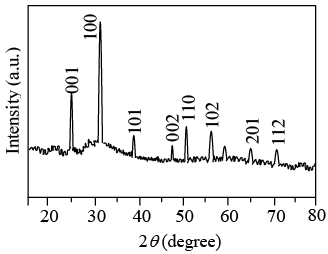
A recorder automatically plots the intensity of the diffracted beam as the counter moves on a Goniometer circle. Figure shows an x-ray diffraction recorder chart for the intensity of the diffracted beam verses the diffraction angle 2θ for a powdered pure metal specimen.
➤ Characteristics of the Bragg’s law:
(i). It is the consequence of the periodicity of the space lattice.
(ii). The Bragg’s law does not refer to the arrangement or basis of the atoms associated with the lattice points.
(iii). For a given order n and spacing d, the angle θ decreases with decrease in the wavelength λ.
(iv). The relative intensity of the various orders n of diffraction from a given set of parallel planes is determine by the composition of the basis of the crystal results in the change in d. This in turn changes the phase difference between the interfering waves and hence the resulting amplitude. Being proportional to the square of the amplitude the intensity is therefore affected.
(v). Bragg’s reflection occur only for the wavelength λ ≤ 2d . That’s why crystal cannot diffract visible rays.
(vi). For X-ray photons,
E=hv = hc/λ or 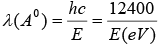
Therefore the energy of X-rays of wavelength 1A0 is 12.4keV.
Electron Diffraction by Crystal
According to de-Broglie, a particle of momentum p (= mv) is associated with a wave of wavelength 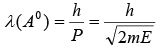
Where h is the Planck constant. M is the mass of the electron and E is the energy of the electron. Since m = 9.1x10-31kg.
Therefore λ(A0) = 12/√E
Thus the energy of electrons of wavelength 1A0 is 144eV.
➤ Characteristic of Electron Diffraction
(i). Incident electrons are not only diffracted by the electrons but also by the nuclei of the atoms of the crystal. So the electron diffraction is much more intense than X-ray diffraction.
(ii). An electron beam has very low penetration power as it experiences repulsion from atomic electrons. Therefore this technique is useful for thin films.
Neutron diffraction by Crystal
Using the de-Broglie relation for neutron (mass m=1.675x10-27kg) the associated wavelength
λ (A0) = 0.28/√E
This shows that the energy associated with neutrons of wavelength 1A0 is approximately 0.08eV. This energy is much less than of X-rays of the same wavelength.
➤ Characteristic of Neutron Diffraction
(i) Neutrons are scattered only by the nuclei of the atoms of the crystal.
(ii) Scattering cross section does not vary with increasing atomic number.
(iii) Lighter elements such as hydrogen and carbon produces strong neutron scattering which is almost absent in X-ray diffraction.
|
91 videos|21 docs|25 tests
|
FAQs on X-Ray Diffraction - Solid State Physics, Devices & Electronics
| 1. What is X-ray diffraction? |  |
| 2. How does X-ray diffraction work? |  |
| 3. What can X-ray diffraction be used for? |  |
| 4. What are the applications of X-ray diffraction in research? |  |
| 5. What are the advantages of X-ray diffraction as a characterization technique? |  |





















