Ampère’s circuital law and Faraday’s law - Class 12 PDF Download

Ampère’s circuital law

Despite its name, Ampère’s circuital law was derived not by André-Marie Ampère, but by James Clerk Maxwell in 1860, and is one of the Maxwell equations of electromagnetism. (Ampère formulated Ampère’s force law, which describes the attractive or repulsive force between two current-carrying wires.)

A magnetic field exerts a force on a straight wire that is carrying current. With Ampère’s circuital law, the strength of the magnetic field can be determined by:

Where:

B = magnetic field (T)

μ₀ = magnetic permeability of air, T-m/A

I = current (A)

r = distance from the wire (m)

When the wire is a loop, the magnetic field causes a force in one direction on one side of the loop, and in the opposite direction on the other side of the loop. This creates a torque, which causes the coil to spin. Note that if direct current is applied, the coil will oscillate back and forth, but will not make complete revolutions – this is the reason DC motors use commutators. Motors that are operated with alternating current (AC motors) don’t exhibit this problem.

Faraday’s law of induction

Faraday’s law of induction is the fundamental law on which electric motors operate. Michael Faraday is credited with discovering induction in 1831, but James Clerk Maxwell described it mathematically and used it as the foundation of his quantitative electromagnetic theory in the 1860s.

Inductance is a property of a device that tells how effectively it induces an emf in another device (or on itself).

Faraday’s law generally states that in a closed coil (loop) of wire, a change in the magnetic environment of the coil causes a voltage, or emf (electromotive force), to be induced in the coil.

The change in magnetic environment can be caused by changing the magnetic field strength, moving the magnet toward or away from the coil, moving the coil into or out of the magnetic field, or rotating the coil in the field.

The induced emf equals the negative rate of change of the magnetic flux, times the number of turns in the coil:

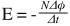
Where:

E = emf (V)

N = number of turns in the coil

Φ = magnetic flux (weber, Wb)

t = time (s)