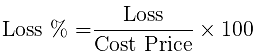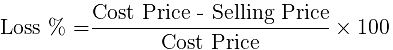Basic Concepts: Profit, Loss & Discount | Quantitative Aptitude (Quant) - CAT PDF Download
Introduction
- In the world of business and trade, understanding profit and loss is essential. For shopkeepers, the relationship between the selling price and cost price determines whether they gain or lose money on a transaction.
- If the selling price is higher than the cost price, the result is a profit. Conversely, if the cost price is greater than the selling price, it leads to a loss.
- In this document, we will dive into the fundamentals of profit and loss, and provide simple strategies to tackle problems related to these concepts effectively.
Basic Terms
1. Cost Price (CP)
1. Cost Price (CP)
The amount paid by a vendor for a product or commodity to purchase it is called a cost price. Also, denoted as CP.
This cost price is further classified into two different categories:
- Fixed Cost: The fixed cost is constant, it doesn’t vary under any circumstances
- Variable Cost: It could vary depending on the number of units
2. Selling Price (SP)
The amount for which the product is sold is called the Selling Price. It is usually denoted as SP. It is also called sale price.
3. Profit and Loss
Profit: When an article is sold for more than the cost of the article, then we say there is a Profit or Gain.
- Profit or Gain = S.P - C.P
Loss: When an article is sold for less than the cost of the article, then we say there is a Loss.
- Loss = C.P - S.P
The formula for the profit and loss percentage is:
- Profit percentage = (Profit / Cost Price) x 100
- Loss percentage = (Loss / Cost price) x 100
Important: If the selling price of X articles is equal to the cost price of Y articles, then the net profit percentage is given by
Example 1: Brijesh purchased a book for Rs.1260 and sold it to Rakesh for Rs.1320. Rakesh sold it to Kishore for Rs.1400. Who gained more and by how much?
Sol:For Brijesh,
The cost price of the book= Rs.1260.
The selling price = Rs.1320. So, the profit = Rs.1320 — Rs.1260 = Rs.60.
For Rakesh,
The cost price of the book= Rs.1320.
The selling price of the book= Rs.1400. So, the profit = Rs.1400 — Rs.1320 = Rs.80.
Clearly, Rakesh gained more than Brijesh. The difference in profits = Rs.80 — Rs.60 = Rs.20.
Thus, Rakesh gained Rs.20 more than Brijesh.
Example 2: If the selling price of 10 articles is the same as the cost price of 11 articles, find the profit or loss percent.
Sol: Let the cost price of 1 article be Re. 1
Therefore, the C.P. of 10 article = Rs. 10
Also, the C.P. of 11 articles = Rs. 11
Hence, Selling price (S.P.) of 10 articles = Rs. 11
Therefore, the profit percent = profit and loss 2Shortcut:
Here X= 10 and Y=11, therefore, profit percent = profit and loss 2
Important: Profit and Loss are always calculated with cost price as the base.
4. Marked Price (MP)
It is the price at which an item is marked for sale.
Markup: It refers to the difference between the cost price of a product and its selling price, expressed either as a percentage or a fixed amount. It's the extra amount added to the cost price to ensure a profit is made when the product is sold.
- Marked Price = CP + Mark up
- Marked Price = CP + % Mark up on CP
For example, if a shop buys a product for $50 (cost price) and sells it for $70 (selling price), the markup is: 70−50=20
The markup percentage is: (20/50)x100 = 40%
5. Discount
Discounts are reductions in the marked price made by the seller. In case of no discount, SP=MP. However, if a discount is offered, then SP<MP.
- Discount = Marked Price – Selling Price
- Discount Percentage = (Discount/Marked price) x 100
Types of Costs
In any business dealing, there is a situation of selling and buying of products and services. From the seller's point of view, his principal interest, apart from maximizing the sales price of a product/service, is to minimize the costs associated with the selling of that product/service. The costs that a businessman/trader faces in the process of day-to-day business transactions can be subdivided into three basic categories:
1. Direct Costs or Variable Costs
- This is the cost associated with direct selling of a product/service.
- In other words, this is the cost that varies with every unit of the product sold.
- If the variable cost of selling a pen for ₹20 is ₹5, then the variable cost for selling 10 units of the same pen is 10x5=₹50.(That means the part of the cost that varies directly for every additional unit of the product sold is called direct or variable cost)
- Typical examples of direct costs are raw material used in producing one unit of the product, wages to labor in producing one unit of the product when the wages are given on a piece rate basis, etc.
- In the case of traders, the cost price per unit bought is also a direct cost i.e. every such expense that can be tied down to every additional unit of the product sold is a direct cost).
2. Indirect Costs (Overhead Costs) or Fixed Costs
- There are some types of costs that have to be incurred irrespective of the number of items sold and are called as fixed or indirect costs.
- For example, irrespective of the number of units of a product sold, the rent of the corporate office is fixed. Now, whether the company sells 10 units or 100 units, this rent is fixed and is hence a fixed cost.
- Other examples of indirect or fixed costs are salaries to executives and managers, rent for office, office telephone charges, and office electricity charges. Apportionment of indirect (or fixed) costs: fixed costs are apportioned equally among each unit of the product sold.
- Thus, if in units of a product are sold, then the fixed cost to be apportioned to each unit sold is given by

3. Semi Variable Costs
- Some costs are such that they behave as fixed costs under normal circumstances but have to be increased when a certain level of sales figure is reached.
- For instance, if the sales increase to such an extent that the company needs to take up an additional office space to accommodate the increase in work due to the increase in sales then the rent for the office space becomes a part of the semi-variable cost.
Margin and Break-Even Point
Margin and Break-Even Point
Concept of Margin
The difference between the value of the selling price and the variable cost for a product is known as the margin or the contribution of the product.
- This margin goes towards the recovery of the fixed costs incurred in selling the product/service.
Concept of Break-Even Point
The break-even point is defined as the volume of sale at which there is no profit or no loss.
- In other words, the sales value in terms of the number of units sold at which the company breaks even is called the break-even point.
- This point is also called the break-even sales.
- Break-even-sales = Fixed costs/Margin per unit
- Since for every unit of the product, the contribution goes towards recovering the fixed costs, as soon as a company sells more than the break-even sales, the company starts earning a profit. Conversely, when the sales value in terms of the number of units is below the break-even sales, the company makes losses.
- Example,
Suppose that a pen shop has to pay a rent of ₹1000 per month and salaries of ₹4000 to the assistants. Also suppose that this pen shop sells only one variety of pen for 15 each.
Further, the direct cost (variable cost) in buying one pen is ₹2.50 per pen, then the margin is (₹5-₹2.50) = ₹2.50 per pen. - Now, break-even sales will be given by:
Break-even-sales = Fixed costs/Margin per unit
= 5000/2.5
= 2000 pens. - Hence, the pen shop breaks-even on a monthly basis by selling 2000 pens.
Selling every additional pen after the 2000 pen goes towards increasing the profit of the shop. Also, in the case of the shop incurring a loss, the number of pens that are left to be sold to break even will determine the quantum of the loss.
Formulae to Remember
- Profit = (Actual Sales - Break Even Sales) x Contribution per unit
- Loss = (Break Even Sales -- Actual Sales) x Contribution per unit
Important Formulae


The Concept of Same Selling Price with Profit or Loss
When two products are sold at the same price (say S) in such a way that on one of the products we earn a profit and on the other we incur a loss such that the percentage of profit or loss (say x %) is the same, then for the combined transaction the net result would be a loss.
In such cases the selling price is immaterial. There is always a loss in such transactions.

Example: Two articles are sold at Rs.198 each such that a profit of 10% is made on the first while a loss of 10% is incurred on the other. What would be the net profit/loss on the two transactions combined?
Sol:Article 1: Profit = 10%, Selling price = Rs.198.
⇒ Cost price = 198/1.1 = Rs.180.
Article II: Loss = 10%, Selling price = Rs.198.
⇒ Cost price = 198/0.9 = Rs.220.
Therefore, the total Cost price = Rs.180 + Rs.220 = Rs.400.
Also, Total Selling price = 2 x 198 = Rs.396.
Clearly, on the two transactions together, we have a loss of R5.400 Rs.394 = Rs.4.
Shortcut:
Specific Cases and Rules
- False Weight Calculation
If a product is sold at a false weight, the profit percentage is calculated based on the difference between the true weight and the false weight:
- Net Percentage Profit when there are two successive profits

Where and are the percentages of the two successive profits. - Net Percentage Profit or Loss when there's a profit and a loss

Where is the profit percentage and is the loss percentage. Effective Cost Price Calculation after successive profits

Where is the final selling price after two successive profits.Question for Basic Concepts: Profit, Loss & DiscountTry yourself:A shopkeeper bought a bag for Rs. 800 and sold it for Rs 1000. What is the profit percentage earned by the shopkeeper?View Solution
Dishonest Dealer
- A dishonest dealer is one who claims to sell his product in the welfare of the customer but either he alters weight or he marks up price too high and then gives a discount to attract customers.
- Let us assume that the shopkeeper gains a G% when selling his product.
Therefore,
(100+G)/(100+x) = True weight/ False weight
Here,
G = Overall gain percentage
X = %loss or % gain - Also, another formula that you can remember, in case the shopkeeper sells at the cost price, is:
Gain Percentage =

Example: Let a dishonest shopkeeper sells sugar at Rs 18/kg which he has bought at Rs 15/kg and he is giving 800gm instead of 1000gm. Find his actual profit percentage.
Sol: Here the cost price of the sugar = Rs 15/kg
The selling price = Rs 18/kg.
The profit made by the shopkeeper is of Rs 3 and the profit percentage = 3/15 x 100 = 20%
This will be his total profit if he has actually sold 1 kg sugar. But that is not the case here as he is using the false weight.Now the profit due to wrong weight =
= (200/800)x100 = 25%
The overall profit percentage = {P + Q + (PQ/100)} = [20+25+{(20 x 25)/100}] = 50%You can also attempt this problem by another method.
The cost price of 1kg sugar is Rs 15.
As the shopkeeper is giving only 800gm.
So the cost price of the 800 gm sugar is Rs 12.
Here we have calculated the cost price of 800gm sugar because the shopkeeper is actually selling only 800gm.
He is selling 800 gm sugar for Rs 18 for which he had paid Rs 12.
So he gained Rs 6 and the profit percentage = 6/12 x 100 = 50%The answer in this case is same as calculated above but the first method is more easy than the second one. Just find the individual profits and put the values in {P + Q + (PQ/100)}
The above formula is also valid if the shopkeeper is making losses due to some reason. In that case you will put the negative value for the loss.
Profit Calculation based on Amount Spent and Amount Earned
Profit Calculation based on Amount Spent and Amount Earned
Profit Calculation based on Amount Spent and Amount Earned
- In our everyday lives, we often observe that profit can only be calculated when the number of items bought and sold is the same.
- When this happens, we find the profit or loss by looking at the difference between the money received and the money spent.
- However, there is another way to calculate profit. This method involves comparing the money received with the money spent.
- In this scenario, the profit can be shown by the quantity of goods that remain at the end.
- This is because, in terms of money, the person involved in the transaction has returned all the money they spent.
- Yet, they also have some goods left over after completing the deal.
- These leftover items can be seen as the profit or gain for the person involved.
- Hence, Profit Percentage = (goods left / goods sold) x 100
- For Example A fruit vendor recovers the cost of 25 mangoes by selling 20 mangoes. Find his percentage profit.
Sol: Since money spent = Money earned
therefore, Profit Percent = (Goods Sold/ Goods left) x 100 = (5/20) x 100 = 25%
Solved Problems
To understand the concept let's first open a shop say a local retail stationery shop.
Example 1: Now suppose a student shows up and wants to buy 5 gel pens worth ₹ 5 each. The cost price of one pen is ₹ 4. So, what is the profit earned by the shopkeeper in net terms and its profit percentage?
Sol: This ₹ 5 is the selling price, the price at which the commodity is sold to its buyer. And ₹ 4 is the price at which the shopkeeper has bought these pens from his supplier and this price is known as Cost Price.
Thus, this difference between the price at which the shopkeeper buys his pen and at which it is sold is known as profit/ loss earned. Now if Selling Price > Cost Price then he will earn profit and if Selling Price < Cost Price, then he will earn loss.
Therefore, Profit = Selling Price – Cost Price = ₹ 5 – ₹4 = ₹1 per pen
Now,
i.e.
And consequently, Loss = Cost Price – Selling Price
i.e.
Example 2: Suppose another customer comes to the shop and bought 2 registers worth ₹ 50 each and a pencil box from him. And this time the shopkeeper has earned 40% profit on the registers. He earned a profit of ₹10 on pencil box and the profit% on pencil box is 20%. Then what is the cost price and profit on register and selling price and cost price of pencil box?
Sol: In this case, we are given S.P. = ₹ 50 for each register and profit% = 40%. Let C.P. be x.
⇒ Profit % = {(50 – x)/x} * 100
⇒ 40 = {(50 – x)/x} * 100
⇒ 4x = 500 – 10x
⇒ 14x = 500
⇒ x = 35.71
⇒ Profit = 50 – 35.71 = 14.29What if the profit of 40% is on selling price instead?
⇒ Profit = profit% * S.P = 0.4* 50 = ₹20
C.P. = S.P. – Profit = ₹50 – ₹20 = ₹30Let's now move on to calculate S.P. and C.P. of pencil box. Let C.P. of pencil box be y
∵ Profit % = (profit/ Cost price) *100
⇒ 20 = (10/y) *100
⇒ 2y = 100
⇒ y = ₹ 50
Therefore, S.P. = ₹50 + ₹10 = ₹60
Example 3: Since not many customers showed up on the first day of the shop. Therefore, to popularize the shop the shopkeeper puts up discount of 20% on all the products. The first customer showed up and bought a packet of pencils and 3 erasers still making up a profit of 30% on both items. Then what is the actual cost price of both the items when the pencil is marked as ₹30 and the eraser ₹ 5 each?
What does the underlined marked mean?
Here marked means Marked Price is the price that is offered to customer before discount basically, discount is just difference between marked price and Selling price i.e. Discount = M.P. – S.P.
Sol: In this case, Discount = 0.2 * Price of packet of pencil = 0.2 *30 = ₹ 6
Therefore, S.P = 30 – 6 = ₹ 24
∵ Profit is 30% on C.P., assume C.P. be x
⇒ 0.3 = (24 – x)/x
⇒ 0.3x = 24 – x
⇒ 1.3x = 24
⇒ x = 18.46
Similarly,
Discount = 0.2 * Price of 3 erasers = 0.2* 3*5 = ₹ 3
Hence, S.P. = (3*5) - 3 = ₹ 12
∵ Profit is 30% on C.P., assume C.P. be y
⇒ 0.3 = (12 – y)/y
⇒ 1.3y = 12
⇒ y (C.P. of 3 eraser) = 9.23
Example 4: Consider this situation, the stationery sold a parker pen at a loss of 20% for ₹ 100 and a pack of colored sketch pens at a loss of 15% on S.P. What are the cost price and selling price of both the articles?
Sol: First, let's find out the C.P. and S.P. parker pen,
∵ Loss is 20% on C.P.
Let C.P. be x and S.P. be 100
⇒ S.P. = 0.8 of C.P.
⇒ 100 = 0.8x
⇒ 100/0.8 = x
⇒ 125 = x
For sketch pens,
∵ Loss is 15% on S.P.
Let S.P. be y and C.P. be 100
⇒ Loss = 0.15y
⇒ C.P. = 1.15 y
⇒ 100 = 1.15y
⇒ 100/1.15 = y
⇒ y = ₹ 87
Example 5: A watch dealer incurs an expense of Rs. 150 for producing every watch. He also incurs an additional expenditure of Rs. 30,000, which is independent of the number of watches produced. If he is able to sell a watch during the season, he sells it for Rs. 250. If he fails to do so, he has to sell each watch for Rs. 100. If he is able to sell only 1,200 out of 1,500 watches he has made in the season, then he has made a profit of:
(a) ₹ 90000
(b) ₹ 75000
(c) ₹ 45000
(d) ₹ 60000
This question is not basic and direct as the problems given above. This one came in CAT 2016 paper and you should expect to get this level of questions in the exam. Now let's see how to solve this problem.
Sol: Here, first find out cost he has incurred to produce the watches.
∵ He made 1500 watches costing ₹ 150 each and an additional ₹ 30000 expense on them.
⇒ Total Cost = (1500*150) + 30000 = ₹ 255000
∵ He's able to sell 1200 watches in the season = ₹250 each
So, the revenue earned by him during the season = ₹250 * 1200 = ₹ 300000
Also, the leftover 300 pieces of clocks would have been sold by the watchmaker in off-season = 100 each.
Revenue earned through these 300 watches = 300*100 = ₹ 30000
Total Revenue = ₹ 300000 + ₹30000 = ₹330000
Profit = Revenue - Cost = 330000 - 255000 = ₹ 75000
Example 6: Instead of a meter scale, a cloth merchant uses a 120cm scale while buying, but uses an 80cm scale while selling the same cloth. If he offers a discount of 20% on cash payment, what is his overall profit percentage?
Sol: This question above is a special one with the faulty dealer. Here, the dealer is earning profit by using a false scale.
To solve this problem, first assume that the price of the cloth is ₹ 1/cm
∵ He's using a 120 cm scale.
⇒ C.P. = (100/120) * ₹1 = ₹ 0.8333/cm
∵ This merchant again uses faulty scale to sell the cloth to his customers. He uses a scale that measures 80cm as 100cm i.e. he sells 80cm for ₹100
Now he also gives a discount of 20% on the cloth.
⇒ His mark up price is ₹100/80cm
∵ S.P. = M.P. - M.P. * Discount% = M.P. (1 - Discount%) = (100/80)*(80/100) = ₹1/cm
Therefore, his profit % = (1 – 0.8333)/0.8333 *100 = 20%
|
191 videos|131 docs|110 tests
|
FAQs on Basic Concepts: Profit, Loss & Discount - Quantitative Aptitude (Quant) - CAT
| 1. What are the basic terms related to profit, loss, and discount in financial calculations? |  |
| 2. How do you calculate the margin and break-even point in a business? |  |
| 3. What is the significance of the same selling price with profit or loss in business transactions? |  |
| 4. How can one identify a dishonest dealer in terms of profit calculations? |  |
| 5. How do you calculate profit based on the amount spent and amount earned? |  |

|
Explore Courses for CAT exam
|

|