Ex-9.2, Triangle And Its Angles, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q1) The exterior angles, obtained on producing the base of a triangle both ways are 1040 and 1360. Find all the angles of the triangle.
Solution:
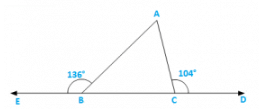
∠ACD = ∠ABC + ∠BAC [Exterior angle property]
Now∠ABC = 1800 − 1360 = 440 [Linera pair]
∠ACB = 1800 − 1040 = 760 [Linera pair]
Now,InΔABC
∠A + ∠ABC + ∠ACB = 1800 [Sum of all angles of a triangle]
⇒ ∠A + 440 + 760 = 1800
⇒ ∠A = 1800 − 440 − 760
⇒ ∠A = 600
Q2) In a triangle ABC, the internal bisectors of ∠B and ∠C meet at P and the external bisectors of ∠B and ∠C meet at Q. Prove that ∠BPC + ∠BQC = 1800.
Solution:
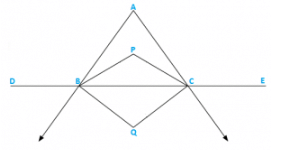
Let ∠ABD = 2x and ∠ACE = 2y
∠ABC = 1800 − 2x [Linera pair]
∠ACB = 1800 − 2y [Linera pair]
∠A + ∠ABC + ∠ACB = 1800 [Sum of all angles of a triangle]
⇒ ∠A + 1800 − 2x + 1800 − 2y = 1800
⇒ − ∠A + 2x + 2y = 1800
⇒ x + y = 900 + 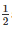 ∠A
∠A
Now in ΔBQC x + y + ∠BQC = 1800 [Sum of all angles of a triangle]
⇒ 900 + 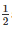 ∠A + ∠BQC = 1800
∠A + ∠BQC = 1800
⇒ ∠BQC = 900 − 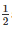 ∠A….(i)
∠A….(i)
and we know that∠BPC = 900 + 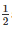 ∠A….(ii)
∠A….(ii)
Adding (i) and (ii) we get ∠BPC + ∠BQC = 1800
Hence proved.
Q3) In figure 9.30, the sides BC, CA and AB of a triangle ABC have been produced to D, E and F respectively. If ∠ACD = 1050 and ∠EAF = 450, find all the angles of the triangle ABC.
Solution:
∠BAC = ∠EAF = 450 [Verticallyopposite angles]
∠ABC = 1050 − 450 = 600 [Exterior angle property]
∠ACD = 1800 − 1050 = 750 [Linear pair]
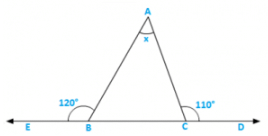
Q4) Compute the value of x in each of the following figures:
(i)
Solution:
∠BAC = 1800 − 1200 = 600 [Linear pair]
∠ACB = 1800 − 1120 = 680 [Linear pair]
∴ x = 1800 − ∠BAC − ∠ACB
= 1800 − 600 − 680 = 520 [Sum of all angles of a triangle]
(ii)
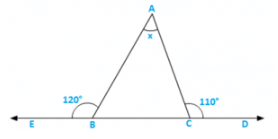
Solution:
∠ABC = 1800 − 1200 = 600 [Linear pair]
∠ACB = 1800 − 1100 = 700 [Linear pair]
∴ e∠BAC = x = 1800 − ∠ABC − ∠ACB
= 1800 − 600 − 700 = 500 [Sum of all angles of a triangle]
(iii)
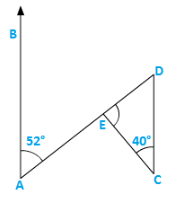
Solution:
∠BAE = ∠EDC = 520 [Alternate angles]
∴∠DEC = x = 1800 − 400 − ∠EDC = 1800 − 400 − 520
= 1800 − 920 = 880 [Sum of all angles of a triangle]
(iv)
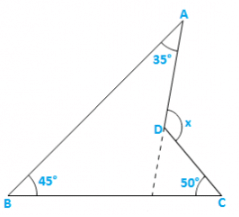
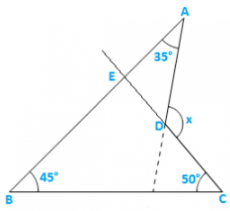
Solution:
CD is produced to meet AB at E.
∠BEC = 1800 − 450 − 500 = 850 [Sumofall angles of a triangle]
∠AEC = 1800 − 850 = 950 [Linear pair]
∴x = 950 + 350 = 1300 [Exterior angle property] .
Q5) In figure 9.35, AB divides ∠DAC in the ratio 1 : 3 and AB = DB. Determine the value of x.
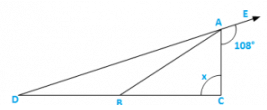
Solution:
Let∠BAD = Z,∠BAC = 3Z
⇒ ∠BDA = ∠BAD = Z (∵AB = DB)
Now∠BAD + ∠BAC + 1080 = 1800 [Linear pair]
⇒ Z + 3Z + 1080 = 1800
⇒ 4Z = 720
⇒ Z = 180
Now, In ΔADC∠ADC + ∠ACD = 1080 [Exterior angle property]
⇒ x + 180 = 1800
⇒ x = 900
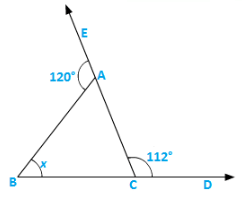
Q6) ABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D = 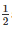 ∠A.
∠A.
Solution:
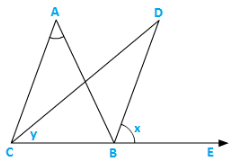
Let ∠ABE = 2x and ∠ACB = 2y ∠ABC = 1800 − 2x [Linear pair]
∴∠A = 1800 − ∠ABC − ∠ACB [ angle sum property]
= 1800 − 1800 + 2x + 2y = 2(x − y)…..(i)
Now,∠D = 1800 − ∠DBC − ∠DCB
⇒ ∠D = 1800 − (x + 1800 − 2x) − y
⇒ ∠D = 1800 − x − 1800 + 2x − y = (x − y) = 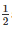 ∠A…..from(i)
∠A…..from(i)
Hence,∠D = 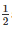 ∠A.
∠A.
Q7) In figure 9.36, AC⊥CE and ∠A:∠B:∠C = 3:2:1,find
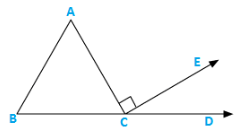
Solution:
∠A:∠B:∠C = 3:2:1
Let the angles be 3x,2x and x
⇒ 3x + 2x + x = 1800 [ angle sum property]
⇒ 6x = 1800
⇒ x = 300 = ∠ACB
∴∠ECD = 1800 − ∠ACB − 900 [Linear pair]
= 1800 − 300 − 900 = 600
∴∠ECD = 600
Q8) In figure 9.37, AM⊥BC and AN is the bisector of ∠A. If ∠B = 650 and ∠C = 330,find ∠ MAN..
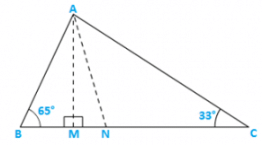
Solution:
Let∠BAN = ∠NAC = x [∵AN bisects ∠A]
∴∠ANM = x + 330 [Exterior angle property]
In ΔAMB ∠BAM = 900 − 650 = 250 [Exterior angle property]
∴∠MAN = ∠BAN − ∠BAM = (x − 25)0
Now in ΔMAN,(x − 25)0 + (x + 33)0 + 900 = 1800 [ angle sum property]
⇒ 2x + 80 = 900
⇒ 2x = 820
⇒ x = 410
∴MAN = x − 250 = 410 − 250 = 160
Q9) In a triangle ABC, AD bisects ∠A and ∠C> ∠B.Provethat ∠ADB > ∠ADC..
Solution:
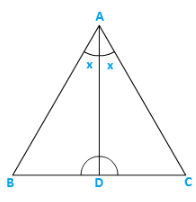
∵∠C>∠B [Given]
⇒ ∠C + x>∠B + x [Adding x on both sides]
⇒ 180° – ∠ ADC>180^{0} – ∠ ADB
⇒ −∠ ADC> – ∠ ADB
⇒ ∠ ADB > ∠ ADC
Hence proved.
Q10) In triangle ABC, BD⊥AC and CE⊥AB. If BD and CE intersect at O, prove that ∠BOC = 1800 − ∠A..
Solution:
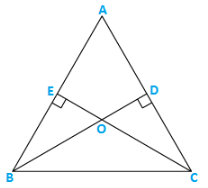
In quadrilateral AEOD
∠A + ∠AEO + ∠EOD + ∠ADO = 3600
⇒ ∠A + 900 + 900 + ∠EOD = 3600
⇒ ∠A + ∠BOC = 1800 [∵∠EOD = ∠BOC vertically opposite angles]
⇒ ∠BOC = 1800 − ∠A
Q11) In figure 9.38, AE bisects ∠CAD and ∠B = ∠C. Prove that AE∥BC.
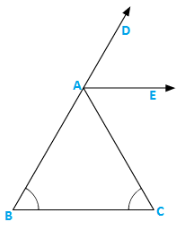
Solution:
Let∠B = ∠C = x
Then,∠CAD = ∠B + ∠C = 2x (exterior angle)
⇒ 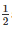 ∠CAD = x
∠CAD = x
⇒ ∠EAC = x
⇒ ∠EAC = ∠C
These are alternate interior angles for the lines AE and BC
∴AE∥BC
Q12) In figure 9.39, AB∥DE.Find∠ACD.
Solution:
Since AB∥DE
∴∠ABC = ∠CDE = 400 [Alternate angles]
∴∠ACB = 1800 − ∠ABC − ∠BAC
= 1800 − 400 − 300 = 1100
∴∠ACD = 1800 − 1100 [Linear pair] = 700
Q13) . Which of the following statements are true (T) and which are false (F) :
(i) Sum of the three angles of a triangle is 180°.
Solution: (i) T
(ii) A triangle can have two right angles.
Solution: (ii) F
(iii) All the angles of a triangle can be less than 60°.
Solution: (iii) F
(iv) All the angles of a triangle can be greater than 60°.
Solution: (iv) F
(v) All the angles of a triangle can be equal to 60°.
Solution: (v) T
(vi) A triangle can have two obtuse angles.
Solution: (vi) F
(vii) A triangle can have at most one obtuse angles.
Solution: (vii) T
(viii) If one angle of a triangle is obtuse, then it cannot be a right angled triangle.
Solution: (viii) T
(ix) An exterior angle of a triangle is less than either of its interior opposite angles.
Solution: (ix) F
(x) An exterior angle of a triangle is equal to the sum of the two interior opposite angles.
Solution: (x) T
(xi) An exterior angle of a triangle is greater than the opposite interior angles.
Solution: (xi) T
Q14) Fill in the blanks to make the following statements true:
(i) Sum of the angles of a triangle is _______ .
(ii) An exterior angle of a triangle is equal to the two ________ opposite angles.
(iii) An exterior angle of a triangle is always ________ than either of the interior opposite angles.
(iv) A triangle cannot have more than _______ right angles.
(v) A triangles cannot have more than _______ obtuse angles.
Solution:
(i) 1800
(ii) Interior
(iii) Greater
(iv) One
(v) One
FAQs on Ex-9.2, Triangle And Its Angles, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What are the angles in a triangle? |  |
| 2. How can I find the measure of an angle in a triangle if I know the measures of the other two angles? |  |
| 3. Can a triangle have two right angles? |  |
| 4. What is the relationship between the sides and angles in a triangle? |  |
| 5. Can a triangle have all three angles greater than 90 degrees? |  |





















