Class 9 Math: Sample Question Paper- 10 (With Solutions) PDF Download
SECTION - A
Question numbers 1 to 20 carry 1 mark each.
Q.1. If A and B are two sets, then A ∩ (A ∩ B) equals
(a) A
(b) B
(c) A ∩ B
(d) φ
Ans. Choice (c) is correct.
As A ∩ B ⊆ A, so A ∩ (A ∩ B) = A ∩ B
Q.2. Degree of the polynomial 4x4 +0x3 + 0x5 + 5x + 7 is
(a) 4
(b) 5
(c) 3
(d) 7
OR
One of the factors of the expression
[x2 - y2 - z2 + 2yz + x + y - z] is:
(a) x - y + z + 1
(b) -x + y + z
(c) x + y - z + 1
(d) x - y - z + 1
Ans. (a)
OR
(a)
∵ Given expression
= x2 - y2 - z2 + 2yz + x + y - z
= x2 - (y2 + z2 - 2yz) + (x + y - z)
= x2 - (y - z)2 + (x + y - z)
= [(x + y - z)(x - y + z)]+(x + y - z)
= [(x + y - z) (x - y + z) + 1]
= (x + y - z) (x - y + z + 1)
One factor of the expression is
(x - y + 2 + 1).
Q.3. Ordinate of a point m positive in:
(a) II and III quadrant
(b) I and II quadrant
(c) I and IV quadrant
(d) II and IV
Ans. (b) I and II quadrant
Q.4. In the given figure, if AC is bisector of ∠BAD such that AB = 3 cm and AC = 5 cm, then CD is equal to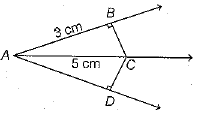
(a) 2 cm
(b) 3 cm
(c) 4 cm
(d) 5 cm
Ans. (c) In ΔABC and ΔADC,
AC = AC [common]
∠BAC = ∠DAC [AC is bisector of ∠BAD]
∠CBA = ∠CDA = 90°
∴ ΔAEC ≌ ΔADC [by AAS]
BC = DC [by CPCT]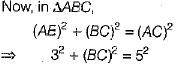
⇒ (BC)2 = 52 - 32 = 25 - 9 = 16
⇒ BC = 4 cm
∴ DC = BC = 4 cm
Q.5. The total number of terms in the expansion of (a3 - 3a2b + 3ab2 - b3)50 is:
(a) 151
(b) 152
(c) 153
(d) None of these
Ans. Choice (a) is correct.
We have, (a3 - 3a2b + 3ab2 - b3)50= {(a - b)3}50 = (a - b)150
We know that the total number of terms in the expansion of (x + a)n is (n + 1).
∴ Total number of terms in the expansion of (a - b)150 is (150 + 1) = 151.
Total number of terms in the expansion of (a — 3a2b + 3ab2 - b3)50 is 151.
Q.6. ABCD is a rhombus such that ∠ACB = 40°. Then ∠ADB is
(a) 40°
(b) 45°
(c) 50°
(d) 60°
Ans. (c)
ABCD is a rhombus such that ∠ACB = 40°.
We know that diagonals of a rhombus bisect each other at right angles.
In right triangle BOC, we have
∠OBC + ∠BOC + ∠BCO = 180°
(Angle sum property of triangle)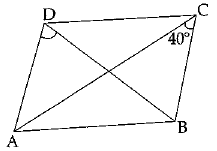
∠OBC =180° - (∠BOC + ∠BCO)
=180° - (90° + 40°) = 50°
∠DBC = ∠OBC = 50°
Now, ∠ADB = ∠DBC [Alt. int. angles]
∠ADB = 50°.
Q.7. In the given figure, area of quadrilateral ABCD is:
(a) 24 cm2
(b) 30 cm2
(c) 36 cm2
(d) 48 cm2
Ans. (c) 36 cm2 [∵ ar(quad. ABCD) = ar(ΔABC) + ar(ΔACD)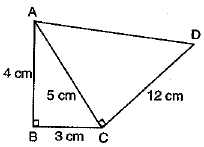
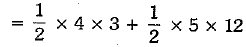
= 6 + 30 = 36 cm5]
Q.8. The sum of all the four angles of a quadrilateral is
(a) 180°
(b) 360°
(c) 540°
(d) 720°
Ans. (b) The sum of all the four angles of a quadrilateral is 360°.
Q.9. The negation of the statement “A square is a rectangle” is
(a) A rectangle is a square.
(b) A rectangle is not a square.
(c) A square is not a rectangle.
(d) A square is always a rectangle.
Ans. Choice (c) is correct.
Because, “A square is not a rectangle” is contradictory to the “A square is a rectangle”. Also because both the statements do not have the same truth.
Q.10. In Fig. if OA = 5 cm, AB = 8 cm and OD is perpendicular to AB , then CD is equal to:
(a) 2 cm
(b) 3 cm
(c) 4 cm
(d) 1 cm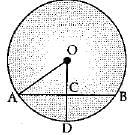
Ans. (a)
Given: OD ⊥ AB and AB is a chord, OA = 5 cm, AB = 8 cm
We know that the perpendicular from the centre of a circle to the chord bisects the chord.
AB ⇒ AC = 4 cm
Now, In Δ AOC
(AO)2 = (OC)2 + (AC)2 (Pythagoras theorem)
(5)2 = (OC)2 + 32
(OC)2= 25 - 16
OC = √9
OC = 3 cm
Now CD = OD - OC = 5 - 3 = 2 cm
Q.11. 101 x 105 = ............ .
Ans. 10605
[∵ 101 x 105 = (100 + 1) (100 + 5) = 10000 + 500 + 100 + 5 = 10605]
Q.12. Two triangles having same base and between same parallel lines, have.............
Ans. If two triangles are on same base and between same parallels lines, then their area is equal area.
Q.13. The number of 4-digit numbers that can formed using the digits 1, 3, 5 and 7 is________
Ans. 24
There can be as many as numbers as there is permutation of four-digits 1, 3, 5, 7 taken all at a time.
∴ The required 4-digits numbers = 41 = 4 x 3 x 2 x 1 = 24
Q.14. The area of a triangle with base 4 cm and height 6 cm is 24 cm2.
Ans. False
Base = 4 cm, height =6 cm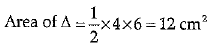
The area of the triangle is 12 cm2 but given area is 24 cm2.
Q.15. P(E) + P(not E) = ......................
Ans. one
Q.16. In the given figure, find ∠BAC.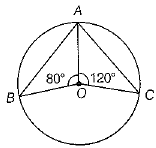
OR
Diagonals AC and BD of a parallelogram ABCD intersect each other at O. If OA = 3 cm and OD = 2 cm, determine the lengths of AC and BD.
Ans. From figure,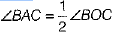
[since, angle subtended at the arc is half of the angle subtended at the centre]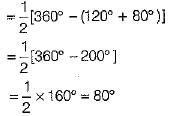
OR
Given, OA = 3 cm and OD = 2 cm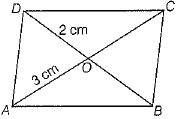
We know that diagonals of a parallelogram bisect each other.
∴ AC = 2 x OA = 6cm and BD = 2 x OD = 4cm
Q.17. What is the real value of a for which 3i3 - 2ai2 + (1 - a)i + 5 is real?
Ans. 3i3 - 2ai2 + (1 - a )i + 5 = 3(i2)(i) - 2a (-1) + (1 - a)i + 5 = 3 (-1)(i) + 2a + (1 - a)t + 5
= -3i + 2a + (1 - a)i + 5 = (2a + 5) + (-3 + 1 - a)i
= -(2a + 5) + (- 2 - a)i.
The complex number is real, so its imaginary part is zero.
∴ - 2 - a = 0 ⇒ a = - 2
Q.18. The angles of a quadrilateral are (4x°), (7x°), (15x°) and (10x°). Find the smallest angle of the quadrilateral.
Ans. 4x + 7x + 15x + 10x = 360° (Angle sum prop.)
x = 10°
Smallest angle = 4x = 40°
Q.19. If every side of a triangle is doubled, then find the per cent increase in area of triangle so formed.
Ans. Let the sides of the given triangle be, a units, b units and c units.
∴ Its area = 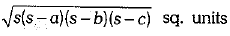
Now, new sides of the triangle are 2a units, 2b units and 2c units.
Thus, its area = 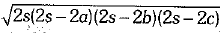 =
= 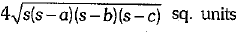
Total increase in are = 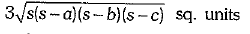
Hence, percent increase = 300%
Q.20. Factorise (x - 2y)3 + (2y - 3z)3 + (3z - x)3.
Ans. Let a = x - 2y, b = 2y - 3z and c = 3z - x
Then, a + b + c = x - 2y + 2y - 3z + 3z - x = 0
∴ a3 + b3 + c3 = 3adc
⇒ (x - 2y)3 + (2y - 3z)3 + (3z - x)3
= 3(x - 2y)(2y - 3z)(3z - x)
SECTION - B
Question numbers 21 to 26 carry 2 marks each.
Q.21. Let A = {9 ,10, 11, 12, 13} and let f : A → N be defined by f(n) = the highest prime factor of n. Find the range off.
OR
If U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, B = {2, 4, 6, 8}, C = {3, 4, 5, 6} and D = {6, 7, 8, 9}, find:
(i) (B - C)'
(ii) (B ∩ D')
Ans. A = {9, 10, 11, 12, 13}
The highest prime factor of 9 is 3, so f(9) = 3
The highest prime factor of 10 is 5, so f(10) = 5
The highest prime factor of 11 is 11, so f(11) = 11
The highest prime factor of 12 is 3, so f(12) = 3
The highest prime factor of 13 is 13, so f(13) = 13
∴ Range of f = {3, 5, 11, 13).
OR
U= {1, 2, 3, 4, 5, 6, 7, 8, 9}, B = {2, 4, 6, 8], C = {3, 4, 5, 6} and D= {6, 7, 8, 9}
B - C = { 2, 4, 6, 8} - {3, 4, 5, 6} = {2, 8}
(B - C)' = U - (B - C) = {1, 2, 3, 4, 5, 6, 7, 8, 9} - {2, 8) = {1, 3, 4, 5, 6, 7, 9}
D' = U - D = {1, 2, 3, 4, 5, 6, 7, 8, 9} - {6, 7, 8, 9} = {1, 2, 3, 4, 5}
(B ∩ D') = {2, 4, 6, 8} ∩ {1, 2, 3, 4, 5} = {2, 4}
Q.22. State any two Euclid's axioms.
Ans. Euclid's axioms
(i) Things which are equal to the same thing are equal to one another.
(ii) If equals are added to equals, the wholes are equal.
Q.23. Wildlife is a part of our environment and conservation of each of its elements is important for ecological balance. Three lighthouse towers are located at points A, B and C on the section of a national forest to protect animals from hunters by the forest department as shown in figure.
How many straight lines can be drawn from A to C? State the Euclid Axiom which states the required result. Give one more Postulate.
Ans. One and only one line can be drawn from A to C.
According to Euclid’s Postulate, “A straight line may be drawn from any point to any other point.” Another Postulate: “A circle may be described with any centre and any radius.”
Q.24. In the given figure, BD = DC and ∠CBD = 40°. Find ∠BAC.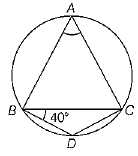
OR
In the given figure, AE = AD and CE = BD.
Prove that ΔAEB ≌ ΔADC.
Ans. In ΔBDC, BD = DC [given]
∴ ∠DCB = ∠CBD = 400 ...(i)
[∵ angles opposite to equal sides are equal]
Also, ∠CBD + ∠BDC + ∠DCB = 1800
∴ 400 + ∠BDC + 400 = 1800 [from Eq. (i)]
⇒ ∠BDC = 1800 - 800 = 1000
As A, B, D and C are four points on a circle.
Therefore, ABDC forms a cyclic quadrilateral.
Hence, ∠A+ ∠D = 180°
[∵ in a cyclic quadrilateral, sum of two opposite angles is equal to two right angles i.e. 180°]
⇒ ∠A+ 100° = 180° [∵ ∠D = ∠BDC = 100°]
∴ ∠A = 80°
OR
Given, AE = AD ...(i)
and CE = BD ...(ii)
On adding Eqs. (i) and (ii), we get
AE+ CE = AD + BD ⇒ AC = AB
Now, in ΔAEB and ΔADC, we have
AE = AD [given]
AB = AC [proved above]
and ∠A = ∠A [common angle]
∴ ΔAEB ≌ ΔADC [by SAS congruence rule] Hence proved.
Q.25. A milkman has 80% milk in his stock of 800 litres of adulterated milk. How much pure milk he should add to his stock to obtain 99% pure milk?
Ans. For desired purity of milk the milkman is free to add any quantity from 800 litres to 2400 litres of 100% pure milk.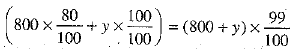
where y litres of 100% pure milk is added to get 99% pure milk.
Now (800 x 80 + 100y) = (800 + y)99
or 100y - 99y = 800 x 99 - 800 x 80
or y = 800 x (99 - 80) = 800 x 19 = 15200
i.e., 15200 litres of 100% milk should be added to get 99% pure milk.
Q.26. In a mathematics test given to 15 students, the following marks are recorded.
41, 39, 48, 52, 46, 62, 54, 40, 96, 52, 98, 40, 42, 52, 60
Find the median and the mode.
Ans. The given data in ascending order is : 39, 40, 40, 41, 42, 46, 48, 52, 52, 52, 54, 60, 62, 96, 98
n = 15 (odd)
Median = 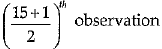
= 8th observation
= 52
Mode = 52, Since it is repeating three times in a data.
SECTION - C
Question numbers 27 to 32 carry 4 marks each.
Q.27. Find domain and range of the real function/defined as 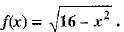
Ans. Here,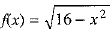 is not defined when 16 - x2 < 0,
is not defined when 16 - x2 < 0,
i.e., when (4 - x)(4 + x) < 0
i.e ., when 4 - x < 0 and 4 + x > 0 Or i .e ., when 4 - x > 0 and 4 + x < 0
i .e ., when 4 < x and x > - 4 Or i. e . , when 4 > x and x < - 4
i. e . , when x > 4 and x > - 4 Or i.e., when x < 4 and x < - 4
i .e ., when x > 4 Or i.e., when x < - 4
⇒ x > 4 or x < - 4
Also for each real number x such that - 4 ≤ x ≤ 4,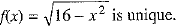
So, domain of the given function = {x ∈ R : - 4 ≤ x ≤ 4}
Further 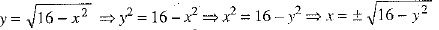
Clearly, x is not defined when (16 - y2) < 0
But, (16 - y2) < 0 ⇒ y > 4 or y < - 4 [For explanation see above]
Also, 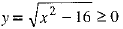
∴ Range of the function = {y ∈ R: 0 ≤ y ≤ 4}
Q.28. Draw the graph of the linear equation
x + y = 7
At what points, does the graph cut the x-axis and the y-axis?
Ans. x + y = 7
When x = 0 then y = 7
When y = 0 then x = 7
When x = 3 then y = 4
Table for x + y = 7 is

Intercept on x-axis and y- axis = 7 units.
They intersect the x-axis at (7, 0) and the y-axis j at (0, 7).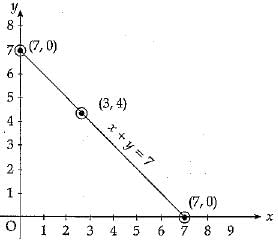
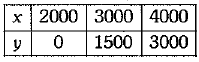
Q.29. Awareness, amongst citizens for protection of environment and making pollution free air: Participatory role of residents in the welfare of the society. Resident Welfare Association of a colony Chandan Nagar decided to develop flower beds in the park of the colony and then plant Jasmine plants in the flower beds. The difference of three times the money spent on flower beds and two times the money spent on Jasmine plants was INR 6000. Write a linear equation in two variables for this above mention situation and draw its graph.
Ans. Let money spent on flower beds be INR x and that on Jasmine plants be INR y.
Thus, the required equation as per statement of the question is:
3x - 2y = 6000
Table of solution is: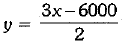
Required graph is shown alongside.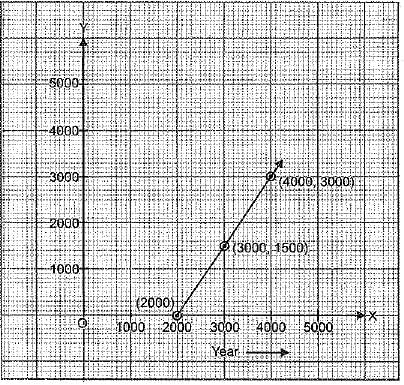
Q.30. Construct a ΔABC whose perimeter is 8.2 cm and the base angles are 45° and 60°.
Ans. Steps of construction
(i) First, draw PQ = 8.2 cm.
(ii) At point P, construct ∠RPQ = 60° and at point Q, construct ∠SQP = 45°.
(iii) Draw bisector of ∠RPQ and ∠SQP, which intersect each other at point A.
(iv) Join AP and AQ.
(v) Draw perpendicular bisector of AP which intersects PQ at point B and also draw perpendicular bisector of AQ which intersects PQ at point C.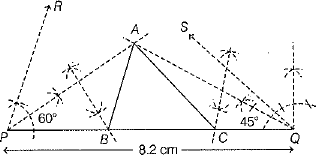
(vi) Join AB and AC.
Thus, we get the required ΔABC.
Q.31. A farmer buys a used tractor for INR 12000. He pays INR 6000 cash and agrees to pay the balance in annual instalments of INR 500 plus 12% interest on the unpaid amount. How much will tractor cost him?
Or
Let 5 be the sum, P the product and R the sum of the reciprocals of n terms of a G.P. Prove that P2Rn = Sn.
Ans. Total amount paid by the farmer
= Cash down payment at the time of purchase + Sum of the balance in annual
instalments of INR 500 plus 12% interest on the unpaid amount ...(1)
Total cost of the used tractor = INR 12000
Balance cost of the used tractor = INR 12000 - INR 6000 (cash paid at the time of purchase) = INR 6000
Balance payment made at the end of 1 year by the farmer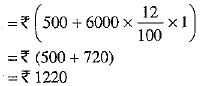
Balance payment made at the end of 2nd year by the farmer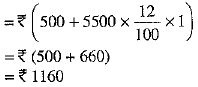
Balance payment made at the end of 3rd year by the farmer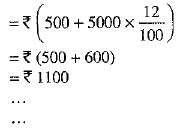
and so on.
Thus, the payments form an A.P. whose first term, a = INR 1220 and common difference, d= -60 (1160 -1220) and n = be the number of instalments obtained by dividing INR 6000 by INR 500.
Therefore, the A.P. is
1220, 1160, 1100, 1040, 980, 920, 860, 800, 740, 680, 620, 560
Now, from (1), we get
Total cost of a used tractor will be = 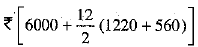
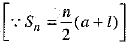
= INR [6000 + 6( 1780)]
= INR [6000 + 10680]
= INR 16680
OR
Let a, ar, ar2, . . . , arn-1 be the given G.P., then
S = Sum of terms of a G.P.
⇒ S = a + ar+ ar2+ ... + arn-1
⇒ 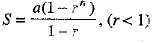
⇒ 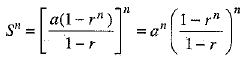 ...(i)
...(i)
P = Product of n terms of a G.P.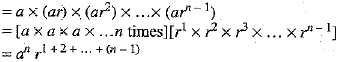
⇒ 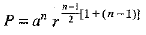
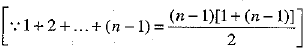
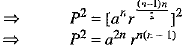 ...(2)
...(2)
and R = Sum of reciprocals of n terms of a G.P.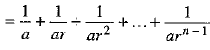
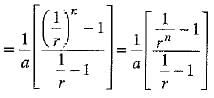
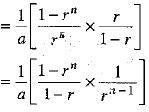
⇒ 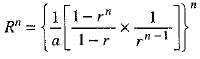
⇒ 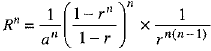 ...(3)
...(3)
Multiplying (2) and (3), we get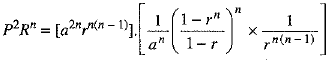
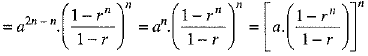
= Sn.
Q.32. If O is the circumcentre of a ΔABC and OD ⊥ BC, then prove that ∠BOD = ∠BAC.
OR
In the given figure, C and D are points on the semicircle with AB as diameter. If ∠BAD = 75° and ∠DBC = 40°, find ∠ABD, ∠ACB and ∠BDC.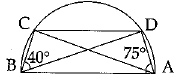
Ans.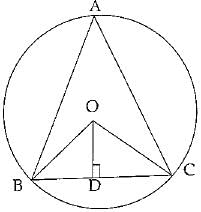
Given: OD ⊥ BC
Proof: In ΔOBD and ΔOCD
OB = OC (radii)
OD = OD (Common)
∠ODB = ∠ODC (90°)
ΔOBD ≌ ΔOCD (RHS congruence)
∠BOD = ∠COD (c.p.c.t)
But ∠BOC = 2∠BOD
2 ∠BAC = 2 ∠BOD
(Angle subtended by an arc of a circle at the centre is twice the one subtended at the circumcentre)
or ∠BOD = ∠BAC
OR
Since AB is the diameter.
∠ADB = 90° (angle in the semi circle)
In ΔADB
∠ABD + ∠ADB +∠BAD = 180° (angle sum property)
∠ABD + 90° +75° = 180°
∠ABD = 15°
Also, ∠ACB = 90° (angle in the semi circle)
∠BCD + ∠BAD = 180°(opp. ∠s of circlic quad. are supplementary)
∠BCD + 75° = 180°
∠BCD = 180° -75° = 105°
In ΔBDC
∠BDC +∠BCD + ∠DBC = 180° (angle sum property)
∠BDC + 105° + 40°= 180°
∠BDC = 180° - 145°
= 35°
Q.33. Construct an isosceles triangle whose perimeter is 10 cm and altitude is 3 cm.
Ans. Given: In ΔABC,
AB + BC + CA = 10 cm,
AB = AC and AM ⊥ BC, AM = 3 cm
Required: To construct ΔABC.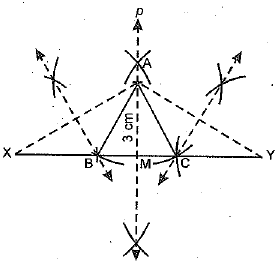
Steps of construction:
1. Draw any line segment XY = 10cm.
2. Draw ‘p’ the perpendicular bisector of XY and let it intersect XY in M.
3. Cut-off AM = 3 cm.
4. Join AX and AY.
5. Draw the perpendicular bisectors of XA and YA and let they intersect XY in B and C.
6. Join AB and AC.
Thus, ΔABC is the required triangle.
Q.34. If f(x) = x2 - 5x + 1, then evaluate f(2) - f(-1) + f(1/3).
Ans. Given, f(x) = x2 - 5x + 1 ...(i)
On putting x = 2 in Eq. (i), we get
f(2) = (2)2 - 5 x 2 + 1 = 4 - 10 + 1
= 5 - 10 = - 5
On putting x = -1 in Eq. (i), we get
f(-1) = (-1)2 - 5 x (-1) +1 = 1 + 5 + 1 = 7
On putting x = 1/3 in Eq. (i), we get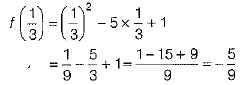
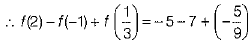
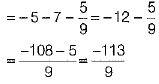
SECTION - D
Question numbers 33 to 36 carry 6 marks each.
Q.35. In a town of 10.000 families it was found that 40% families buy newspaper A, 20% families buy newspaper B, 10% families buy newspaper C, 5% families buy A and B, 3% of families buy B and C and 4% buy A and C. If 2% of families buy all the three newspapers, find:
(a) the number of families which buy newspaper A only.
(b) the number of families which buy none of A, B and C.
Ans. Total families in a town = 10,000 = U(say)
n(A) = Number of families buy newspaper A
= 40% of 10,000
= 4,000
n(B) = Number of families buy newspaper B
= 20% of 10,000
= 2,000
n(C) = Number of families buy newspaper C
= 10% of 10,000
= 1,000
n(A ∩ B) = Number of families buy both newspapers A and B
= 5% of 10,000
= 500
n(B ∩ C) = Number of families buy both newspapers B and C
= 3% of 10,000
= 300
n(A ∩ C) = Number of families buy both newspapers A and C
= 4% of 10,000
= 400
n(A ∩ B ∩ C) = Number of families buy all the newspaper A, and B and C
= 2% of 10,000
= 200
(a) The number of families which buy newspaper A only is
n(A ∩ B' ∩ C)
= n(A) - n[A ∩ (B ∪ C)']
= n(A) - n(A ∩ (B ∪ C)]
=n(A) -n[(A ∩ B) ∪(A ∩ C)] [P ∩ (Q ∪ R)= (P ∩ Q) ∪ (P ∩ R)]
= n(A) - [n(A ∩ B) + n(A ∩ C) - n(A ∩ B) ∩ (A ∩ Q)] [n (P ∪ Q)] = n(P) + n( Q) - n(P ∩ Q)]
= n( A) -n ( A ∩ B ) - n( A ∩ C) + n(A ∩ B ∩ C)
= 4,000 - 500 - 400 + 200
=3,300
Q.36. If the polynomial ax3 + 4x2 + 3x - 4 and x3 - 4 x + a leave the same remainder when divided by (x - 3). Find the value of a.
OR
Factorise x3 + 6x2 + 11x + 6
Ans. Let p(x) = ax3 + 4x2 + 3x - 4
and q(x) = x3 - 4x + a
Put, x - 3 = 0 or x = 3 in p(x) and q(x)
p(3) = a(3)3 + 4(3)2 + 3 x 3 - 4
= 27a + 36 + 9 - 4
= 27a + 41
q(3) = (3)3 - 4(3) + a
= 27 - 12 + a
= 15 + a
According to the question,
p(3) = q(3)
⇒ 27 a + 41 = 15 + a
⇒ 27 a - a = 15 - 41
⇒ 26a = -26
⇒ a = -1.
OR
Let p(x) = x3 + 6x2 + 11x + 6
p(-1) = 0 ⇒ (x + 1) is a factor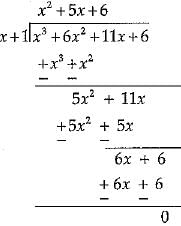
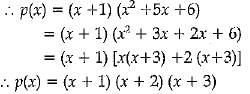
Q.37. In a ΔABC, the sides AB and AC are produced to D and E respectively. The bisectors of ∠DBC and ∠ECB intersect at a point O. Prove that 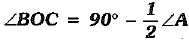
OR
In the given figure, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that 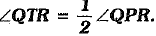
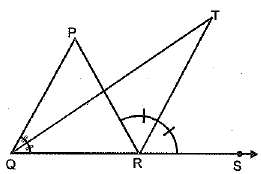
Ans. Given: The sides AB and AC of ΔABC are produced to D and E respectively. The bisectors of ∠DBC and ∠ECB intersect each other at O.
To Prove: 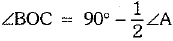
Proof: We know that,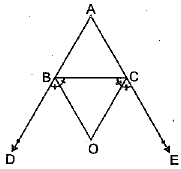
∠ABC + ∠CBD = 180° [linear pair]
⇒ 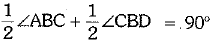
⇒ 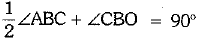 [∵ BO is the bisector of ∠CBD]
[∵ BO is the bisector of ∠CBD]
⇒ 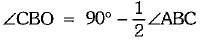 ...(i)
...(i)
Similarly, ∠ACB + ∠BCE = 180° [linear pair]
⇒ 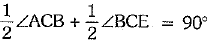
⇒ 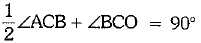 [∵ CO is the bisector of ∠BCE]
[∵ CO is the bisector of ∠BCE]
⇒ 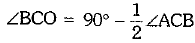 ...(ii)
...(ii)
In ΔOBC,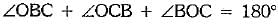 [sum of ∠s of a Δ is 180°]
[sum of ∠s of a Δ is 180°]
⇒ 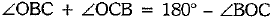
⇒ 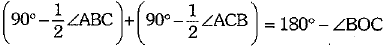 [using (i) and (ii)]
[using (i) and (ii)]
⇒ 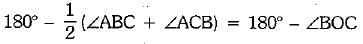
⇒ 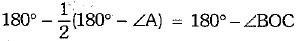
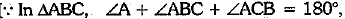
∴ 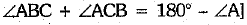
⇒ 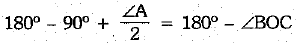
⇒ 
⇒ 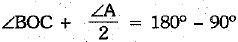
⇒ 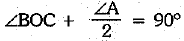
⇒ 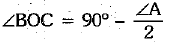
OR
In ΔPQR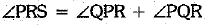 ...(i) [ext. ∠ = sum of int. opp. ∠s]
...(i) [ext. ∠ = sum of int. opp. ∠s]
Again, in ΔTQR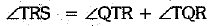 ...(ii) [ext. ∠ = sum of int. opp. ∠s]
...(ii) [ext. ∠ = sum of int. opp. ∠s]
Now, QT and RT are the bisectors of ∠PQR and ∠PRS respectively.
⇒ 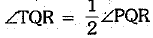 ...(iii)
...(iii)
and 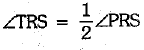 ...(iv)
...(iv)
From (i), we have
⇒ 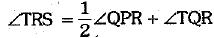 ...(v) [using (iii) and (iv)]
...(v) [using (iii) and (iv)]
From (ii) and (v), we have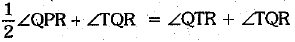
⇒ 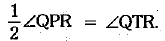
Q.38. Find
(i) the lateral or curved surface area of a closed cylindrical petrol storage tank, which is 4.2 m in diameter and 4.5 m in high.
(ii) how much steel was actually used, if 1/12 of the steel actually used was wasted in making the tank?
Ans. (i) We have, cylindrical petrol storage tank having diameter, d = 4.2 m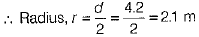
and height, h = 4.5m
Curved surface area of a closed cylindrical petrol storage tank = 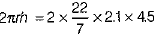
= 44 x 0.3 x 4.5 = 59.4 m2
(ii) Now, total surface area of cylindrical tank
= Curved surface area + 2πr2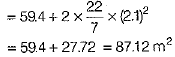
Let x m2 be the area of the steel.
Since, 1/12 of the actual steel used was wasted. Therefore, the area of the steel, which was actually used for making the tank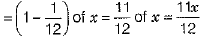

Hence, actually steel used in making a tank is 95.04 m2.
Q.39. The second, third and fourth terms in the binomial expansion (x + a)n are 240, 720 and 1080 respectively. Find x, a and n.
OR
The sum of the coefficients of the first three terms in the expansion 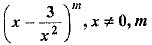 being a natural number, is 559. Find the term of the expansion containing x3.
being a natural number, is 559. Find the term of the expansion containing x3.
Ans. In the expansion of (x + a)n, (r + 1)th term is given by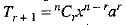
In the expansion of (x + a)n, we have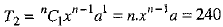 ...(1)
...(1)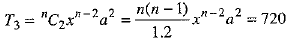 ...(2)
...(2)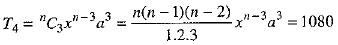 ...(3)
...(3)
Dividing (2) by (1), we have ...(4)
...(4)
Dividing (3) by (2), we have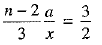 ...(5)
...(5)
Dividing (5) by (4), we get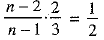
⇒ 4n - 8 = 3n - 3 ⇒ n = 5
Putting the value of n in (1) and (2), we get
5 x4a = 240 ...(6)
⇒ 10x3a2 = 720 ...(7)
Dividing (7) by square of (6) to eliminate a, we get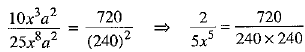
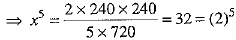
⇒ x = 2 ...(8)
Putting the value of x in (6), we get
5(2)4a = 240 ⇒ 5 x 16 x a = 240 ⇒ a = 3
Hence, x = 2, a = 3 and k = 5.
OR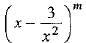
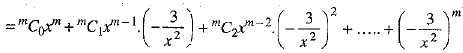 [Expanding by binomial theorem]
[Expanding by binomial theorem]
Thus, the coefficients of the first three terms of 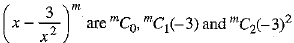 respectively.
respectively.
It is given that the sum of the coefficients of the first three terms in the expansion 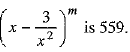
∴ 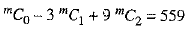
⇒ 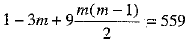
⇒ 2 - 6m + 9m2 - 9m = 1118
⇒ 9m2 - 15m - 1116 = 0
⇒ 3m2 - 5m - 372 = 0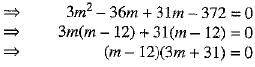
⇒ 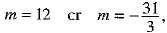 reject it, m being a natural number
reject it, m being a natural number
Now, 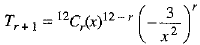
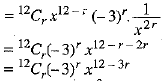
We need the term containing x3, so put 3 = 12 - 3r ⇒ 3r = 9 or r = 3
Thus, the required term is 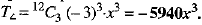
Q.40. The number of literate females in the age group (10-57 years) in a village are given below: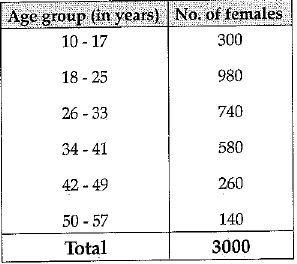
Draw a histogram to represent the data above.
Ans. Consider the classes 10 - 17 and 18 - 25.
The lower limit of 18 - 25 = 18
The upper limit of 10 - 17 = 17
The difference = 18 - 17 = 1
∴ Half the difference = 1/2 = 0.5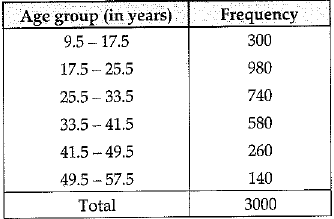
The histogram of given data is shown below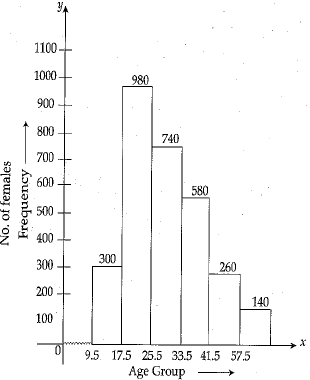
FAQs on Class 9 Math: Sample Question Paper- 10 (With Solutions)
| 1. What is the format of the Class 9 Math Sample Question Paper-10? |  |
| 2. Can you provide an example of a frequently asked question from the Class 9 Math Sample Question Paper-10? |  |
| 3. How many questions are there in the Class 9 Math Sample Question Paper-10? |  |
| 4. Are the solutions provided for all the questions in the Class 9 Math Sample Question Paper-10? |  |
| 5. Is the complexity level of the questions in the Class 9 Math Sample Question Paper-10 appropriate for Class 9 students? |  |














