Properties of Parallelograms | Mathematics (Maths) Class 9 PDF Download
| Table of contents |

|
| Introduction |

|
| What are the Properties of a Parallelogram? |

|
| Theorems on Properties of a Parallelogram |

|
| Solved Examples |

|
Introduction
The properties of a parallelogram help us to identify a parallelogram from a given set of figures easily and quickly. Before we learn about the properties of a parallelogram, let us first know about parallelograms.It is a four-sided closed figure with opposite sides and equal angles. A parallelogram is a convex polygon with 4 edges and 4 vertices. The opposite sides are equal and parallel; the opposite angles are also equal.
Let's learn more about the properties of parallelograms in detail in this lesson.
What are the Properties of a Parallelogram?
Understanding the properties of parallelograms helps to easily relate the angles and sides of a parallelogram. Also, the properties are helpful for calculations in problems relating to the sides and angles of a parallelogram.The four important properties of a parallelogram are as follows.
- Opposites sides of a parallelogram are equal and parallel to each other.
- Opposite angles are equal. ∠A= ∠C, and ∠B = ∠D
- All the angles of a parallelogram add up to 360o. ∠A + ∠B + ∠C + ∠D = 360o.
- The consecutive angles of a parallelogram are supplementary
- ∠A + ∠B = 180o
- ∠B + ∠C = 180o
- ∠C + ∠D = 180o
- ∠D + ∠A = 180o
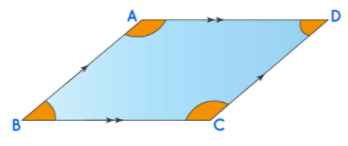 Sides and Angles of a Parallelogram
Sides and Angles of a Parallelogram
Theorems on Properties of a Parallelogram
The theorems on properties of a parallelogram are helpful to define the rules for working across the problems on parallelograms. The properties relating to the sides and angles of a parallelogram can all be easily understood and applies to solve various problems. Further, these theorems are also supportive to understand the concepts in other quadrilaterals. Four important theorems relating to the properties of a parallelogram are given below:- Opposite sides of a parallelogram are equal
- Opposite angles of a parallelogram are equal
- Diagonals of a parallelogram bisect each other
- One pair of opposite sides is equal and parallel in a parallelogram
Theorem 1: A diagonal of a parallelogram divides it into two congruent triangles.
First, we will recall the meaning of a diagonal. Diagonals are line segments that join the opposite vertices. In parallelogram PQRS, PR and QS are the diagonals. The properties of diagonals of a parallelogram are as follows:
- Diagonals of a parallelogram bisect each other. OQ =OS and OR = OP
- Each diagonal divides the parallelogram into two congruent triangles, so, ΔRSP ≅ ΔPQR and ΔQPS ≅ ΔSRQ.
- Parallelogram Law: The sum of the squares of the sides is equal to the sum of the squares of the diagonals. PQ2+QR2+RS2+SP2 = QS2+PR2
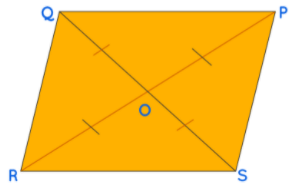 Diagonals of a Parallelogram
Diagonals of a Parallelogram
Theorem 2: In a Parallelogram the Opposite Sides Are Equal. This means, in a parallelogram, the opposite sides are equal.
Given: ABCD is a parallelogram.
To Prove: The opposite sides are equal, AB=CD, and BC=AD.
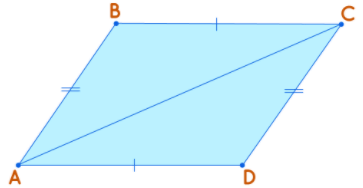
Proof: In parallelogram ABCB, compare triangles ABC and CDA. In these triangles AC = CA (common sides). Also ∠BAC =∠DCA (alternate interior angles), and ∠BCA = ∠DAC (alternate interior angles). Hence by the ASA criterion, both the triangles are congruent and the corresponding sides are equal. Therefore we have AB = CD, and BC = AD.
Theorem 3: If the opposite sides in a quadrilateral are equal, then it is a parallelogram. If AB = CD and BC = AD in the given quadrilateral ABCD, then it is a parallelogram.
Given: The opposite sides in a quadrilateral ABCD are equal, AB = CD, and BC = AD.
To Prove: ABCD is a parallelogram.
Proof: In the quadrilateral ABCD we are given that AB = CD, and AD = BC. Now compare the two triangles ABC, and CDA. Here we have AC = AC (Common sides), AB = CD (since alternate interior angles are equal), and AD = BC (given). Thus by the SSS criterion both the triangles are congruent, and the corresponding angles are equal. Hence we can conclude that ∠BAC = ∠DCA, and ∠BCA = ∠DAC. Therefore AB // CD, BC // AD, and ABCD is a parallelogram.
Theorem 4: In a Parallelogram, the Opposite Angles Are Equal.
Given: ABCD is a parallelogram, and ∠A, ∠B, ∠C, ∠D are the four angles.
To Prove: ∠A =∠C and ∠B=∠D
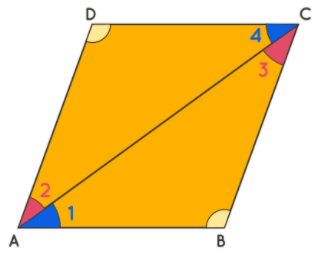
Proof: Let us assume that ABCD is a parallelogram.
Now compare triangles ABC, and CDA.
Here we have AC=AC (common sides), ∠1=∠4 (alternate interior angles), and ∠2=∠3 (alternate interior angles).
Thus, the two triangles are congruent, which means that ∠B=∠D. Similarly, we can show that ∠A=∠C.
This proves that opposite angles in any parallelogram are equal.
Theorem 5: If the opposite angles in a quadrilateral are equal, then it is a parallelogram.
Given: ∠A=∠C and ∠B=∠D in the quadrilateral ABCD. To Prove: ABCD is a parallelogram.
Proof: Assume that ∠A = ∠C and ∠B = ∠D in the parallelogram ABCD given above.
We have to prove that ABCD is a parallelogram.
We have: ∠A + ∠B + ∠C + ∠D = 360º;2(∠A + ∠B) =360º; ∠A + ∠B = 180º.
This must mean that AD // BC. Similarly, we can show that AB//CD. Hence, AD//BC, and AB//CD.
Therefore ABCD is a parallelogram.
Theorem 6: Diagonals of a Parallelogram Bisect Each Other. That means, in a parallelogram, the diagonals bisect each other.
Given: PQTR is a parallelogram. PT and QR are the diagonals of the parallelogram.
To Prove: The diagonals PT, and RQ bisect each other. PE=ET and ER=EQ
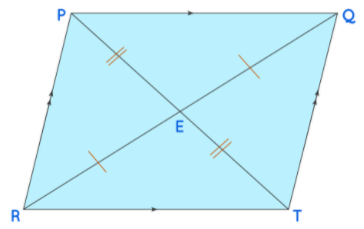
Proof: First, let us assume that PQTR is a parallelogram. Compare triangles RET, and triangle PEQ.
We have PQ = RT (opposite sides of the parallelogram), ∠QRT = ∠PQR (alternate interior angles), and ∠PTR = ∠QPT (alternate interior angles).
By the ASA criterion, the two triangles are congruent, which means that PE = ET, and RE = EQ.
Thus, the two diagonals PT, and RQ bisect each other, and PE=ET and ER=EQ
Theorem 7: If the diagonals in a quadrilateral bisect each other, then it is a parallelogram. In the quadrilateral PQTR, if PE=ET and ER=EQ, then it is a parallelogram.
Given: The diagonals PT and QR bisect each other.
To Prove: PQRT is a parallelogram.
Proof: Suppose that the diagonals PT and QR bisect each other. Compare triangle RET, and triangle PEQ once again.
We have: RE = EQ, ET = PE (Diagonals bisect each other), ∠RET =∠PEQ (vertically opposite angles).
Hence by the SAS criterion, the two triangles are congruent.
This means that ∠QRT = ∠PQR, and ∠PRT = ∠QPT .
Hence, PQ//RT, and RT//QT.
Thus PQRT is a parallelogram.
Theorem 8: The line segment joining the mid-points of two sides of a triangle is parallel to the third side.
Proof: You can prove this theorem using the following clue:
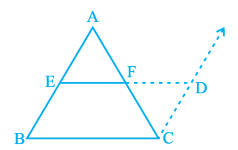
Observe above figure in which E and F are mid-points of AB and AC respectively and CD || BA.
∆ AEF ≅ ∆ CDF (ASA Rule)
So, EF = DF and BE = AE = DC (Why?)
Therefore, BCDE is a parallelogram. (Why?)
This gives EF || BC.
In this case, also note that EF = 1/2ED = 1/2BC.
Can you state the converse of Theorem 8.8? Is the converse true?
You will see that converse of the above theorem is also true which is stated as below:
Theorem 9: The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.
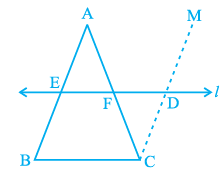
In above figure, observe that E is the mid-point of AB, line l is passing through E and is parallel to BC and CM || BA.
Solved Examples
Example 1: A parallelogram ABCD and a rectangle ABPQ are on the same base AB and between the same parallels AB and CQ. If AB = 8 cm and AQ = 6 cm, find the area of ||gmABCD.Sol: A rectangle is a parallelogram in which each angle is 90° and parallelogram on the same base and between same parallels are equal in area.

∴ ar. (||gmABCD) = ar. (rectangle ABPQ)
But ar. (||gmABPQ) = AB×AQ
= (8 × 6) cm2 = 48 cm2
∴ Area of parallelogram ABCD = 48 cm2.
Example 2: In a parallelogram ABCD, AB = 8 cm. The altitudes corresponding to sides AB and AD are respectively 4 m and 5 cm. Find AD.
Sol: We know that the area of a parallelogram = Base × Corresponding altitude.
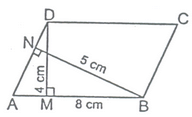
∴ Area of parallelogram ABCD = AD × BN = AB × DM
⇒ AD × 5 = 8 × 4
⇒ AD = 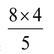
= 6.4 cm.
Example 3: ABCD is a quadrilateral and BD is one its diagonals as shown in figure. Show that ABCD is a parallelogram and find its area.
Sol: In ΔABD and ΔCDB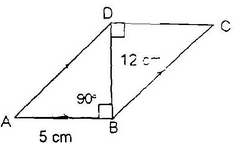
∠ABD = ∠CBD = 90o (alternate interior angles are equal)
∠ADB = ∠CBD
∠BDA = ∠BDC
Hence, ABCD is a parallelogram.
Now, area of parallelogram ABCD = (base ×corresponding altitude)
⇒area of parallelogram ABCD = AB × BD = 5 ×12 sq. units = 60 sq. cms.
Example 4: Prove that parallelograms on the same base and between the same parallel lines are equal in area.
Sol: Given: Two parallelogram ABCD and PBCQ having same base BC and between the same parallel lines BC and AQ.
To Prove: ar(parallelogram ABCD)= ar (parallelogram PBCQ)
Proof: In triangles ABP and DCQ,
∠BAP = ∠CDQ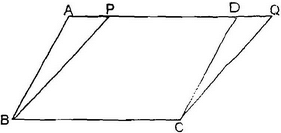
(Corresponding angles when AQ intersects parallel lines AB and DC).
∠BPA = ∠CDQ
(Corresponding angles when AQ intersects parallel lines BP and CQ).
AB = DC (Opposite sides of a parallelogram)
∴ΔABP ≅ ΔDCQ (AAS)
Hence area ΔABP = area ΔDCQ
or, area ΔABP + area BPDC = area ΔDCQ + area Δ BPDC
∴ar (parallelogram ABCD) = ar (parallelogram PBCQ).
|
40 videos|471 docs|57 tests
|
FAQs on Properties of Parallelograms - Mathematics (Maths) Class 9
| 1. What are the main properties of a parallelogram? |  |
| 2. How can you prove that a quadrilateral is a parallelogram? |  |
| 3. What is the significance of the diagonals in a parallelogram? |  |
| 4. Are the opposite angles in a parallelogram always equal? |  |
| 5. How do the properties of a parallelogram apply in real-life situations? |  |
















