RD Sharma Solutions Ex-6.4, (Part -1), Factorization Of Polynomials, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
In each of the following, use factor theorem to find whether polynomial g(x) is a factor of polynomial f(x) , or not : (1 – 7)
Q1. f(x) = x3–6x2+11x–6,g(x) = x–3
Sol :
Here , f(x) = x3–6x2+11x–6
g(x) = x – 3
To prove that g(x) is the factor of f(x) ,
we should show ⇒ f(3) = 0
here , x – 3 = 0
⇒ x = 3
Substitute the value of x in f(x)
f(3) = 33–6∗(3)2+11(3)–6
= 27 – (6*9) + 33 – 6
= 27 – 54 + 33 – 6
= 60 – 60
= 0
Since, the result is 0 g(x) is the factor of f(x)
Q2. f(x) = 3x4+17x3+9x2–7x–10,g(x) = x+5
Sol :
Here , f(x) = 3x4+17x3+9x2–7x–10
g(x) = x + 5
To prove that g(x) is the factor of f(x) ,
we should show ⇒ f(-5) = 0
here , x + 5 = 0
⇒ x = -5
Substitute the value of x in f(x)
f(−5)=3(−5)4+17(−5)3+9(−5)2–7(−5)–10
= (3 * 625) + (12 * (-125)) +(9*25) + 35 – 10
= 1875 – 2125 + 225 + 35 – 10
= 2135 – 2135
= 0
Since, the result is 0 g(x) is the factor of f(x)
Q3. f(x) = x5+3x4–x3–3x2+5x+15,g(x) = x+3
Sol :
Here , f(x) = x5+3x4–x3–3x2+5x+15
g(x) = x + 3
To prove that g(x) is the factor of f(x) ,
we should show ⇒ f(-3) = 0
here , x + 3 = 0
⇒ x = -3
Substitute the value of x in f(x)
f(−3)=(−3)5+3(−3)4–(−3)3–3(−3)2+5(−3)+15
= -243 + 243 + 27 – 27 – 15 + 15
= 0
Since, the result is 0 g(x) is the factor of f(x)
Q4. f(x) = x3–6x2–19x+84,g(x)=x–7
Sol :
Here , f(x) = x3–6x2–19x+84
g(x) = x – 7
To prove that g(x) is the factor of f(x) ,
we should show ⇒ f(7) = 0
here , x – 7 = 0
⇒ x = 7
Substitute the value of x in f(x)
f(7) = 73–6(7)2–19(7)+84
= 343 – (6*49) – (19*7) + 84
= 342 – 294 – 133 + 84
= 427 – 427
= 0
Since, the result is 0 g(x) is the factor of f(x)
Q5. f(x) = 3x3+x2–20x+12,g(x) = 3x–2
Sol :
Here , f(x)=3x3+x2–20x+12
g(x) = 3x – 2
To prove that g(x) is the factor of f(x) ,
we should show ⇒ 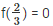
here , 3x – 2 = 0
⇒ 3x = 2
⇒ x = 2/3
Substitute the value of x in f(x)
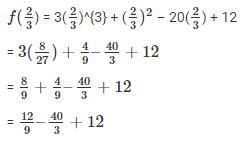
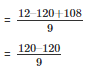
= 0
Since, the result is 0 g(x) is the factor of f(x)
Q6. f(x) = 2x3–9x2+x+13,g(x) = 3–2x
Sol :
Here , f(x) = 2x3–9x2+x+13
g(x) = 3 – 2x
To prove that g(x) is the factor of f(x) ,
To prove that g(x) is the factor of f(x) ,
we should show ⇒ f(3/2) = 0
here , 3 – 2x = 0
⇒ -2x = -3
⇒ 2x = 3
⇒ x = 3/2
Substitute the value of x in f(x)
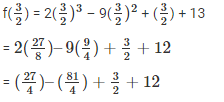
Taking L.C.M
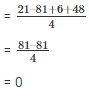
Since, the result is 0 g(x) is the factor of f(x)
Q7. f(x) = x3–6x2+11x–6,g(x) = x2–3x+2
Sol :
Here , f(x) = x3–6x2+11x–6
g(x) = x2–3x+2
First we need to find the factors of x2–3x+2
⇒ x2–2x–x+2
⇒ x(x – 2) -1(x – 2)
⇒ (x – 1) and (x – 2) are the factors
To prove that g(x) is the factor of f(x) ,
The results of f(1) and f(2) should be zero
Let , x – 1 = 0
x = 1
substitute the value of x in f(x)
f(1) = 13–6(1)2+11(1)–6
= 1 – 6 + 11 – 6
= 12 – 12
= 0
Let , x – 2 = 0
x = 2
substitute the value of x in f(x)
f(2) = 23–6(2)2+11(2)–6
= 8 – (6 * 4) + 22 – 6
= 8 – 24 + 22 – 6
= 30 – 30
= 0
Since, the results are 0 g(x) is the factor of f(x)
Q8. Show that (x – 2) , (x + 3) and (x – 4) are the factors of x3–3x2–10x+24
Sol :
Here , f(x) = x3–3x2–10x+24
The factors given are (x – 2) , (x + 3) and (x – 4)
To prove that g(x) is the factor of f(x) ,
The results of f(2) , f(-3) and f(4) should be zero
Let , x – 2 = 0
⇒ x = 2
Substitute the value of x in f(x)
f(2) = 23–3(2)2–10(2)+24
= 8 – (3 * 4) – 20 + 24
= 8 – 12 – 20 + 24
= 32 – 32
= 0
Let , x + 3 = 0
⇒ x = -3
Substitute the value of x in f(x)
f(-3) = (−3)3–3(−3)2–10(−3)+24
= -27 – 3(9) + 30 + 24
= -27 – 27 + 30 + 24
= 54 – 54
= 0
Let , x – 4 = 0
⇒ x = 4
Substitute the value of x in f(x)
f(4) = (4)3–3(4)2–10(4)+24
= 64 – (3*16) – 40 + 24
= 64 – 48 – 40 + 24
= 84 – 84
= 0
Since, the results are 0 g(x) is the factor of f(x)
Q9. Show that (x + 4) , (x – 3) and (x – 7) are the factors of x3–6x2–19x+84
Sol :
Here , f(x) = x3–6x2–19x+84
The factors given are (x + 4) , (x – 3) and (x – 7)
To prove that g(x) is the factor of f(x) ,
The results of f(-4) , f(3) and f(7) should be zero
Let, x + 4 = 0
⇒ x = -4
Substitute the value of x in f(x)
f(-4) = (−4)3–6(−4)2–19(−4)+84
= -64 – (6 * 16) – ( 19 * (-4)) + 84
= -64 – 96 + 76 + 84
= 160 – 160
= 0
Let, x – 3 = 0
⇒ x = 3
Substitute the value of x in f(x)
f(3) = (3)3–6(3)2–19(3)+84
= 27 – (6 * 9) – ( 19 * 3) + 84
= 27 – 54 – 57 + 84
= 111 – 111
= 0
Let, x – 7 = 0
⇒ x = 7
Substitute the value of x in f(x)
f(7) = (7)3–6(7)2–19(7)+84
= 343 – (6 * 49) – ( 19 * 7) + 84
= 343 – 294 – 133 + 84
= 427 – 427
= 0
Since, the results are 0 g(x) is the factor of f(x)
Q10. For what value of a is (x – 5) a factor of x3–3x2+ax–10
Sol :
Here, f(x) = x3–3x2+ax–10
By factor theorem
If (x – 5) is the factor of f(x) then , f(5) = 0
⇒ x – 5 = 0
⇒ x = 5
Substitute the value of x in f(x)
f(5) = 53–3(5)2+a(5)–10
= 125 – (3 * 25) + 5a – 10
= 125 – 75 + 5a – 10
= 5a + 40
Equate f(5) to zero
f(5) = 0
⇒ 5a + 40 = 0
⇒ 5a = -40
⇒ 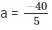
= -8
When a= -8 , (x – 5) will be factor of f(x)
Q11. Find the value of a such that (x – 4) is a factor of 5x3–7x2–ax–28
Sol :
Here, f(x) = 5x3–7x2–ax–28
By factor theorem
If (x – 4) is the factor of f(x) then , f(4) = 0
⇒ x – 4 = 0
⇒ x = 4
Substitute the value of x in f(x)
f(4) = 5(4)3–7(4)2–a(4)–28
= 5(64) – 7(16) – 4a – 28
= 320 – 112 – 4a – 28
= 180 – 4
Equate f(4) to zero, to find a
f(4) = 0
⇒ 180 – 4a = 0
⇒ -4a = -180
⇒ 4a = 180
⇒ a = 180/4
⇒ a = 45
When a = 45 , (x – 4) will be factor of f(x)
Q12. Find the value of a, if (x + 2) is a factor of 4x4+2x3–3x2+8x+5a
Sol :
Here, f(x) = 4x4+2x3–3x2+8x+5a
By factor theorem
If (x + 2) is the factor of f(x) then , f(-2) = 0
⇒ x + 2 = 0
⇒ x = -2
Substitute the value of x in f(x)
f(-2) = 4(−2)4+2(−2)3–3(−2)2+8(−2)+5a
= 4(16) + 2(-8) – 3( 4) – 16 + 5a
= 64 – 16 – 12 – 16 + 5a
= 5a + 20
equate f(-2) to zero
f(-2) = 0
⇒ 5a + 20 = 0
⇒ 5a = -20
⇒ 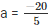
⇒ a = -4
When a = -4 , (x + 2) will be factor of f(x)
Q13. Find the value of k if x – 3 is a factor of k2x3–kx2+3kx–k
Sol :
Let f(x) = k2x3–kx2+3kx–k
From factor theorem if x – 3 is the factor of f(x) then f(3) = 0
⇒ x – 3 = 0
⇒ x = 3
Substitute the value of x in f(x)
f(3) = k2(3)3–k(3)2+3k(3)–k
= 27k2–9k+9k – k
= 27k2–k
= k(27k – 1)
Equate f(3) to zero, to find k
⇒ f(3) = 0
⇒ k(27k – 1) = 0
⇒ k = 0 and 27k – 1 = 0
⇒ k = 0 and 27k = 1
⇒ k = 0 and k = 12/7
When k = 0 and 12/7 , (x – 3) will be the factor of f(x)
FAQs on RD Sharma Solutions Ex-6.4, (Part -1), Factorization Of Polynomials, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the importance of factorization of polynomials in mathematics? |  |
| 2. How can I factorize a polynomial using the common factor method? |  |
| 3. What are the different methods of factorizing polynomials? |  |
| 4. Can all polynomials be factorized? |  |
| 5. How can factorization of polynomials be applied in real-life situations? |  |





















