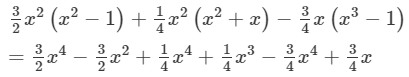RD Sharma Solutions for Class 8 Math Chapter 6 - Algebraic Expressions and Identities (Part-3) | RD Sharma Solutions for Class 8 Mathematics PDF Download
Question 1: Find the following product:
2a3(3a + 5b)
Answer 1: To find the product, we will use distributive law as follows:
2a3(3a+5b)=2a3×3a+2a3×5b=(2×3)(a3×a)+(2×5)a3b=(2×3)a3+1+(2×5)a3b=6a4+10a3b2a33a+5b=2a3×3a+2a3×5b=2×3a3×a+2×5a3b=2×3a3+1+2×5a3b=6a4+10a3b
Thus, the answer is 6a4+10a3b6a4+10a3b.
Question 2: Find the following product:
−11a(3a + 2b)
Answer 2: To find the product, we will use distributive law as follows:
−11a(3a+2b)=(−11a)×3a+(−11a)×2b=(−11×3)×(a×a)+(−11×2)×(a×b)=(−33)×(a1+1)+(−22)×(a×b)=−33a2−22ab-11a3a+2b=-11a×3a+-11a×2b=-11×3×a×a+-11×2×a×b=-33×a1+1+-22×a×b=-33a2-22ab
Thus, the answer is −33a2−22ab-33a2-22ab.
Question 3: Find the following product:
−5a(7a − 2b)
Answer 3: To find the product, we will use distributive law as follows:
−5a(7a−2b)=(−5a)×7a+(−5a)×(−2b)=(−5×7)×(a×a)+(−5×(−2))×(a×b)=(−35)×(a1+1)+(10)×(a×b)=−35a2+10ab-5a7a-2b=-5a×7a+-5a×-2b=-5×7×a×a+-5×-2×a×b=-35×a1+1+10×a×b=-35a2+10ab
Thus, the answer is −35a2+10ab-35a2+10ab.
Question 4: Find the following product:
−11y2(3y + 7)
Answer 4: To find the product, we will use distributive law as follows:
−11y2(3y+7)=(−11y2)×3y+(−11y2)×7=(−11×3)(y2×y)+(−11×7)×(y2)=(−33)(y2+1)+(−77)×(y2)=−33y3−77y2
Thus, the answer is −33y3−77y2.
Question 5: Find the following product:
6x/5 (x3+y3)6x5(x3+y3)
Answer 5: To find the product, we will use distributive law as follows:
6x/5 (x3+y3)
=6x/5×x3+6x/5×y3
=6/5×(x×x3)+6/5×(x×y3)
=6/5×(x1+3)+6/5×(x×y3)
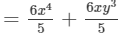
Thus, the answer is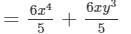 .
.
Question 6: xy(x3 − y3)
Answer 6: To find the product, we will use the distributive law in the following way:
xy(x3−y3)=xy×x3−xy×y3=(x×x3)×y−x×(y×y3)=x1+3y−xy1+3=x4y−xy4xyx3-y3=xy×x3-xy×y3=x×x3×y-x×y×y3=x1+3y-xy1+3=x4y-xy4
Thus, the answer is x4y−xy4x4y-xy4.
Question 7: Find the following product:
0.1y(0.1x5 + 0.1y)
Answer 7: To find the product, we will use distributive law as follows:
0.1y(0.1x5+0.1y)=(0.1y)(0.1x5)+(0.1y)(0.1y)=(0.1×0.1)(y×x5)+(0.1×0.1)(y×y)=(0.1×0.1)(x5×y)+(0.1×0.1)(y1+1)=0.01x5y+0.01y20.1y0.1x5+0.1y=0.1y0.1x5+0.1y0.1y=0.1×0.1y×x5+0.1×0.1y×y=0.1×0.1x5×y+0.1×0.1y1+1=0.01x5y+0.01y2
Thus, the answer is 0.01x5y+0.01y20.01x5y+0.01y2.
Question 8: Find the following product:
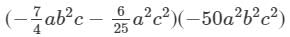
Answer 8: To find the product, we will use distributive law as follows:
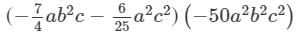
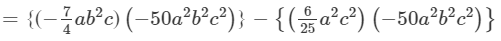
={{−7/4×(−50)}(a×a2)×(b2×b2)×(c×c2)}−{(625)(−50)(a2×a2)×(b2)×(c2×c2)}
={−7/4×(−50)}(a1+2b2+2c1+2)−{(6/25)(−50)(a2+2b2c2+2)}
=175/2 a3b4c3−(−12a4b2c4)
=175/2 a3b4c3+12a4b2c4
Thus, the answer is 175/2 a3b4c3+12a4b2c41752a3b4c3+12a4b2c4.
Question 9: Find the following product:
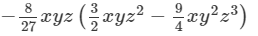
Answer 9: To find the product, we will use the distributive law in the following way:
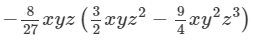
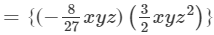
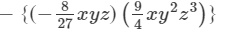
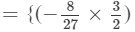 (x×x)×(y×y)×(z×z2)}−
(x×x)×(y×y)×(z×z2)}−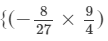 (x×x)×(y×y2)×(z×z3)}
(x×x)×(y×y2)×(z×z3)}
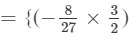 (x1+1y1+1z1+2)}−
(x1+1y1+1z1+2)}− 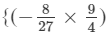 (x1+1y1+2z1+3)}
(x1+1y1+2z1+3)}
23y+7=-11y2×3y+-11y2×7=-11×3y2×y+-11×7×y2=-33y2+1+-77×y2=-33y3-77y2
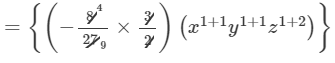 -
-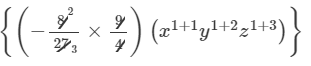
=−4/9 x2y2z3+2/3 x2y3z4
Thus, the answer is −4/9 x2y2z3+2/3 x2y3z4
Question 10: Find the following product:
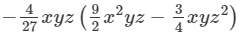
Answer 10: To find the product, we will use distributive law as follows:
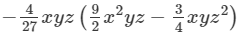
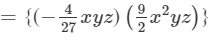
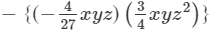
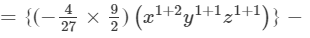
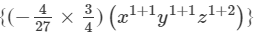
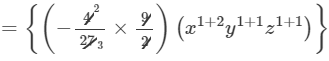
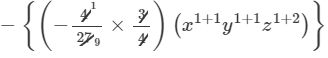
=−2/3 x3y2z2+1/9 x2y2z3
Thus, the answer is −2/3 x3y2z2+1/9 x2y2z3
Question 11: Find the following product:
1.5x(10x2y − 100xy2)
Answer 11: To find the product, we will use distributive law as follows:
1.5x(10x2y−100xy2)=(1.5x×10x2y)−(1.5x×100xy2)=(15x1+2y)−(150x1+1y2)=15x3y−150x2y2Thus, the answer is 15x3y−150x2y215x3y-150x2y2.
Question 12: Find the following product:
4.1xy(1.1x − y)
Answer 12: To find the product, we will use distributive law as follows:
4.1xy(1.1x−y)=(4.1xy×1.1x)−(4.1xy×y)={(4.1×1.1)×xy×x}−(4.1xy×y)=(4.51x1+1y)−(4.1xy1+1)=4.51x2y−4.1xy2Thus, the answer is 4.51x2y−4.1xy24.51x2y-4.1xy2.
Question 13: Find the following product:
250.5xy (xz+y/10)xz+y10
Answer 13: To find the product, we will use distributive law as follows:
250.5xy(xz+y/10)=250.5xy×xz+250.5xy×y/10=250.5x1+1yz+25.05xy1+1=250.5x2yz+25.05xy2Thus, the answer is 250.5x2yz+25.05xy2250.5x2yz+25.05xy2.
Question 14: Find the following product:
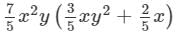
Answer 14: To find the product, we will use distributive law as follows:
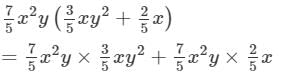
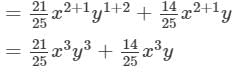
Thus, the answer is 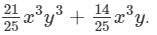
Question 15: Find the following product:
4/3 a(a2 + b2 − 3c2)43a(a2 + b2 - 3c2)
Answer 15: To find the product, we will use distributive law as follows:
4/3 a(a2+b2−3c2)=4/3 a×a2+4/3 a×b2−4/3 a×3c2=4/3 a1+2+4/3 ab2−4ac2=4/3 a3+4/3 ab2−4ac2
Thus, the answer is 4/3 a3+4/3 ab2−4ac2
Question 16: Find the product 24x2 (1 − 2x) and evaluate its value for x = 3.
Answer 16: To find the product, we will use distributive law as follows:
24x2(1−2x)=24x2×1−24x2×2x=24x2−48x1+2=24x2−48x324x21-2x=24x2×1-24x2×2x=24x2-48x1+2=24x2-48x3
Substituting x = 3 in the result, we get:
24x2−48x3=24(3)2−48(3)3=24×9−48×27=216−1296=−1080 Thus, the product is (24x2−48x3) and its value for x = 3 is (−1080)(24x2-48x3) and its value for x = 3 is (-1080).
Question 17: Find the product −3y(xy + y2) and find its value for x = 4 and y = 5.
Answer 17: To find the product, we will use distributive law as follows:
−3y(xy+y2)=−3y×xy+(−3y)×y2=−3xy1+1−3y1+2=−3xy2−3y3Substituting x = 4 and y = 5 in the result, we get:
−3xy2−3y3=−3(4)(5)2−3(5)3=−3(4)(25)−3(125)=−300−375=−675 Thus, the product is (−3xy2−3y3-3xy2-3y3), and its value for x = 4 and y = 5 is (−-675).
Question 18: Multiply −3/2 x2y3 by (2x − y)-32x2y3 by (2x - y) and verify the answer for x = 1 and y = 2.
Answer 18: To find the product, we will use distributive law as follows:
−3/2 x2y3×(2x−y)=(−3/2 x2y3×2x)−(−3/2 x2y3×y)=(−3x2+1y3)−(−3/2 x2y3+1)=−3x3y3+3/2 x2y4
Substituting x = 1 and y = 2 in the result, we get:
−3x3y3+3/2 x2y4=−3(1)3(2)3+3/2 (1)2(2)4=−3×1×8+3/2 ×1×16=−24+24=0Thus, the product is −3x3y3+3/2 x2y4-3x3y3+32x2y4, and its value for x = 1 and y = 2 is 0.
Question 19: Multiply the monomial by the binomial and find the value of each for x = −1, y = 0.25 and z = 0.05:
(i) 15y2(2 − 3x)
(ii) −3x(y2 + z2)
(iii) z2(x − y)
(iv) xz(x2 + y2)
Answer 19: (i) To find the product, we will use distributive law as follows:
15y2(2−3x)=15y2×2−15y2×3x=30y2−45xy2Substituting x = −-1 and y = 0.25 in the result, we get: 30y2−45xy2=30(0.25)2−45(−1)(0.25)2=30×0.0625−{45×(−1)×0.0625}=30×0.0625−{45×(−1)×0.0625}=1.875−(−2.8125)=1.875+2.8125=4.6875 (ii) To find the product, we will use distributive law as follows:
−3x(y2+z2)=−3x×y2+(−3x)×z2=−3xy2−3xz2 Substituting x = −-1, y = 0.25 and z = 0.05 in the result, we get:
−3xy2−3xz2=−3(−1)(0.25)2−3(−1)(0.05)2=−3(−1)(0.0625)−3(−1)(0.0025)=01875+0.0075=0.195 (iii) To find the product, we will use distributive law as follows:
z2(x−y)=z2×x−z2×y=xz2−yz2z2x-y=z2×x-z2×y=xz2-yzSubstituting x = −-1, y = 0.25 and z = 0.05 in the result, we get:
xz2−yz2=(−1)(0.05)2−(0.25)(0.05)2=(−1)(0.0025)−(0.25)(0.0025)=−0.0025−0.000625=−0.003125 (iv) To find the product, we will use distributive law as follows:
xz(x2+y2)=xz×x2+xz×y2=x3z+xy2z Substituting x = −-1, y = 0.25 and z = 0.05 in the result, we get:
x3z+xy2z=(−1)3(0.05)+(−1)(0.25)2(0.05)=(−1)(0.05)+(−1)(0.0625)(0.05)=−0.05−0.003125=−0.053125
Question 20: Simplify:
(i) 2x2(x3 − x) − 3x(x4 + 2x) − 2(x4 − 3x2)
(ii) x3y(x2 − 2x) + 2xy(x3 − x4)
(iii) 3a2 + 2(a + 2) − 3a(2a + 1)
(iv) x(x + 4) + 3x(2x2 − 1) + 4x2 + 4
(v) a(b − c) − b(c − a) − c(a − b)
(vi) a(b − c) + b(c − a) + c(a − b)
(vii) 4ab(a − b) − 6a2(b − b2) − 3b2(2a2 − a) + 2ab(b − a)
(viii) x2(x2 + 1) − x3(x + 1) − x(x3 − x)
(ix) 2a2 + 3a(1 − 2a3) + a(a + 1)
(x) a2(2a − 1) + 3a + a3 − 8
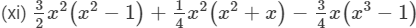
(xii) a2b(a − b2) + ab2(4ab − 2a2) − a3b(1 − 2b)
(xiii) a2b(a3 − a + 1) − ab(a4 − 2a2 + 2a) − b (a3 − a2 − 1)
Answer 20: (i) To simplify, we will use distributive law as follows:
2x2(x3−x)−3x(x4+2x)−2(x4−3x2)=2x5−2x3−3x5−6x2−2x4+6x2=2x5−3x5−2x4−2x3−6x2+6x2=−x5−2x4−2x3(ii) To simplify, we will use distributive law as follows:
x3y(x2−2x)+2xy(x3−x4)=x5y−2x4y+2x4y−2x5y=x5y−2x5y−2x4y+2x4y=−x5y(iii) To simplify, we will use distributive law as follows:
3a2+2(a+2)−3a(2a+1)=3a2+2a+4−6a2−3a=3a2−6a2+2a−3a+4=−3a2−a+4 (iv) To simplify, we will use distributive law as follows:
x(x+4)+3x(2x2−1)+4x2+4=x2+4x+6x3−3x+4x2+4=x2+4x2+4x−3x+6x3+4=5x2+x+6x3+4 (v) To simplify, we will use distributive law as follows:
a(b−c)−b(c−a)−c(a−b)=ab−ac−bc+ba−ca+cb=ab+ba−ac−ca−bc+cb=2ab−2ac (vi) To simplify, we will use distributive law as follows:
a(b−c)+b(c−a)+c(a−b)=ab−ac+bc−ba+ca−cb =ab−ba−ac+ca+bc−cb=0 (vii) To simplify, we will use distributive law as follows:
4ab(a−b)−6a2(b−b2)−3b2(2a2−a)+2ab(b−a)=4a2b−4ab2−6a2b+6a2b2−6b2a2+3b2a+2ab2−2a2b=4a2b−6a2b−2a2b−4ab2+3b2a+2ab2+6a2b2−6b2a2=−4a2b+ab2(viii) To simplify, we will use distributive law as follows:
x2(x2+1)−x3(x+1)−x(x3−x)=x4+x2−x4−x3−x4+x2=x4−x4−x4−x3+x2+x2=−x4−x3+2x2 (ix) To simplify, we will use distributive law as follows:
2a2+3a(1−2a3)+a(a+1)=2a2+3a−6a4+a2+a=2a2+a2+3a+a−6a4=3a2+4a−6a4 (x) To simplify, we will use distributive law as follows:
a2(2a−1)+3a+a3−8=2a3−a2+3a+a3−8=2a3+a3−a2+3a−8=3a3−a2+3a−8 (xi) To simplify, we will use distributive law as follows:
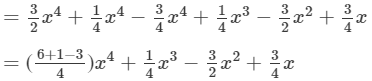
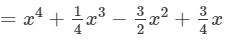
(xii) To simplify, we will use distributive law as follows:
a2b(a−b2)+ab2(4ab−2a2)−a3b(1−2b)=a3b−a2b3+4a2b3−2a3b2−a3b+2a3b2=a3b−a3b−a2b3+4a2b3−2a3b2+2a3b2=3a2b3 (xiii) To simplify, we will use distributive law as follows:
a2b(a3−a+1)−ab(a4−2a2+2a)−b(a3−a2−1)=a5b−a3b+a2b−a5b+2a3b−2a2b−a3b+a2b+b=a5b−a5b−a3b+2a3b−a3b+a2b−2a2b+a2b+b=b